Зона Бріллюена

Зона Бріллюена — характерна для даного типу кристалічної ґратки область оберненого простору із об'ємом ${\frac {(2\pi )^{3}}{V_{0}}}$, де $V_{0}$ — об'єм примітивної комірки в звичайному просторі, і симетрією, яка повністю зберігає симетрію оберненої ґратки кристала.

Найважливішою є перша зона Бріллюена.

Побудова зони Бріллюена

Спочатку будується обернена ґратка для даного кристала. Далі побудова аналогічна побудові комірки Вігнера — Зейтца. Вибирається певний вузол оберненої ґратки. Проводяться лінії до сусідніх вузлів. Через середину кожної лінії проводиться перпендикулярна площина. Найменший об'єм, який виділяється перетином таких площин навколо вибраного вузла, буде першою зоною Бріллюена. Наступний об'єм — другою зоною Бріллюена, і т. д.

Можна сказати, що перша зона Бріллюена, це множина точок в оберненій ґратці, які ближчі до вибраного вузла, ніж до будь-якого іншого.

Приведення до першої зони

Згідно із наслідком теореми Блоха, будь-який квазіімпульс можна привести до першої зони Бріллюена зсувом на певний вектор оберненої ґратки. Тому зазвичай розглядається тільки перша зона Бріллюена.

Значення в теорії кристалів

Хвильові вектори із першої зони Бріллюена — це квантові числа для одноелектронних станів зонної теорії.

Характерні точки зони Бріллюена

Зона Бріллюена кубічної гранецентрованої ґратки

Певні точки високої симетрії в зоні Бріллюена отримали спеціальні позначення.

Центр зони Бріллюена, тобто точка із нульовим значенням квазі-імпульсу позначається грецькою літерою Γ. Якщо електронні зони в зонній структурі кристала пронумеровані, то до літери додають індекс, який відповідає номеру зони: Γ₁, Γ₂ і т. д.

Точки на краю зони Бріллюена позначаються латинськими літерами (X, L і т. д.), а прямі, які ведуть до них грецькими літерами (Δ, Λ і т. д.). Конкретні позначення залежать від будови зони Бріллюена для конкретної кристалічної ґратки.

Приклади

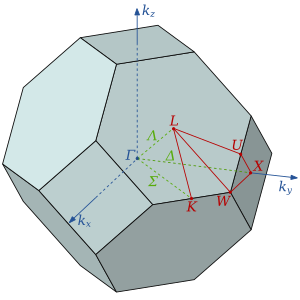
На малюнку праворуч показана перша зона Бріллюена для кубічної гранецентрованої ґратки із характерними позначеннями точок у ній. Червоним виділена ділянка, повторенням якої з врахуванням симетрії, можна заповнити всю зону. Характерні точки суть

• Γ — в центрі зони Бріллюена.
• X — в середині малого квадрата. Лінія, яка веде від Γ до X позначається літерою Δ.
• L — в середині великого шестикутника. Лінія, яка веде від Γ до L позначається Λ.
• K — на середині сторони шестикутника. Лінія, яка веде від Γ до K позначається Σ.

Див. також

• Зонна теорія
• Комірка Вігнера — Зейтца
• Обернений простір

Джерела

• Пінкевич І. П., Сугаков В. Й. Теорія твердого тіла. — К. : ВПЦ "Київський університет", 2006. — 333 с.