Аперіодична ланка


Аперіодична ланка — поняття, що відноситься до Теорії автоматичного керування. Елемент системи автоматичного регулювання.
Аперіодичною ланкою першого порядку називається ланка, що має одну енергетичну ємність, в якій при подачі на вхід ступінчастого впливу вихідна величина приходить до нового усталеного значення за експоненціальним законом.
Аперіодична ланка першого порядку — одноємнісна, інерційна ланка, яка може бути описана диференціальним рівнянням:
,
де — вхідна величина, — вихідна величина, k — коефіцієнт підсилення, T — постійна часу. Це рівняння аперіодичного ланки динамічної системи управління 1-го порядку.
Передавальна функція аперіодичної ланки першого порядку:
- W(p) = k / Тр + 1
Прикладами аперіодичної ланки є тепловий об'єкт, де входом служить, наприклад, витрата палива, а вихідною величиною температура. Інший приклад — технологічна посудина (ємність) з вільним витіканням рідини, тут вхідний сигнал — витрата рідини, що надходить у посудину, а вихідний — її рівень у посудині.
У системах автоматичного керування як аперіодичні ланки можуть виступати двигуни постійного струму, електричний опір і індуктивності і т. д.
Перехідна функція аперіодичної ланки досягає свого сталого значення не відразу, як в підсилювальній ланці, а поступово згідно з експоненціальним (аперіодичним) законом, через що ланка і отримала свою назву. Мірою інерційності ланки є постійна часу Т. Чим менше Т, тим аперіодична ланка ближча за своїми динамічними властивостями до пропорційної. Наприклад, стала часу електронних підсилювачів систем регулювання дорівнює 10-4 — 10-6 сек., тому ці підсилювачі розглядають як пропорційні ланки.
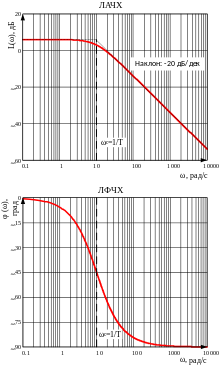
З аналізу амплітудно-частотної характеристики А(w) випливає, що аперіодична ланка має властивість фільтра — добре пропускає сигнали малих частот і погано — великих, із збільшенням частоти зменшується амплітуда вихідного сигналу. Аналіз фазової характеристики φ(ω) показує, що вихідні коливання відстають від вхідних. Це відставання змінюється в межах від 0 до 90о. На частоті зламу ωзл =1/Т φ(ω)=-45о.
Загалом вважається, що майже будь-який об'єкт управління в першому наближенні, дуже грубо, можна описати аперіодичною ланкою 1-го порядку.[1]
Рівняння аперіодичної ланки 2-го порядку має вигляд
,
Дві послідовно з'єднаних аперіодичних ланки 1-го порядку, можуть бути представлені як аперіодична ланка 2-го порядку із загальним коефіцієнтом підсилення.
Передавальна функція аперіодичної ланки 2-го порядку:
- W(p)=k / (Т2р2+Тр+1)
- ↑ Словник з кібернетики / За редакцією В. С. Михалевича. — 2-е видання — К.: 1989. — 751 с., ISBN 5-88500-008-5
- Енциклопедія кібернетики. тт. 1, 2. — К.: Головна редакція УРЕ, 1973. — 584 с.
- Іванов А. О. Теорія автоматичного керування: Підручник. — Дніпропетровськ: Національний гірничий університет. — 2003. — 250 с.
- Папушин Ю. Л., Білецький В. С. Основи автоматизації гірничого виробництва. — Донецьк : Східний видавничий дім, 2007. — 168 с. — ISBN 978-966-317-004-6.




