Двійковий алгоритм обчислення найбільшого спільного дільника
Двійковий алгоритм обчислення НСД, також відомий як алгоритм Стайна або двійковий алгоритм Евкліда — алгоритм, що обчислює найбільший спільний дільник двох невід'ємних цілих чисел. Двійковий алгоритм Евкліда використовує простіші арифметичні операції, ніж звичайний алгоритм Евкліда: він замінює ділення бітовим зсувом, порівняннями та відніманням. Хоча вперше його опублікував ізраїльський фізик і програміст Джозеф Стайн 1967 року[1], алгоритм міг бути відомим ще в першому столітті в Китаї[2].
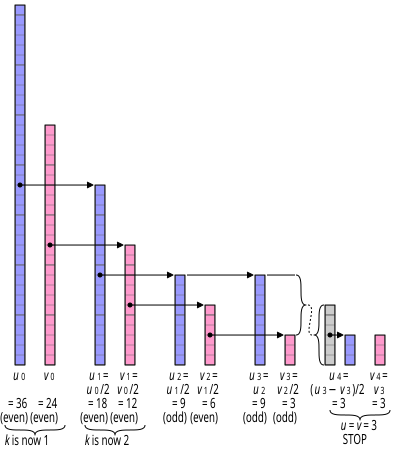
Алгоритм обчислює НСД застосовуючи такі тотожності:
- НСД(0, v) = v, тому що нуль ділиться на всі числа, а v — найбільший дільник числа v. Аналогічно НСД(u, 0) = u. НСД(0, 0) зазвичай невизначено, але зручно вважати, що НСД(0, 0) = 0.
- Якщо u і v парні, то НСД(u, v) = 2·НСД(u/2, v/2), тому що 2 — спільний дільник.
- Якщо u парне, а v непарне, то НСД(u, v) = НСД(u/2, v), тому що 2 не спільний дільник. Аналогічно якщо u непарне, а v парне, то НСД(u, v) = НСД(u, v/2).
- Якщо u і v непарні та u > v, то НСД(u, v) = НСД((u — v)/2, v), якщо ж u < v, то НСД(u, v) = НСД(u, (v — u)/2). Це комбінація одного кроку звичайного алгоритму Евкліда, де на кожному кроці застосовується віднімання, із подальшим застосуванням кроку 3. Різниця двох непарних чисел завжди буде парною, тому ділення на два дає ціле число.
- Кроки 2-4 повторюють поки u не стане рівним v, або поки u не стане 0 (на один крок більше). У будь-якому випадку результат дорівнюватиме 2k×v, де k — кількість спільних дільників 2, знайдених на кроці 2.
У найгіршому випадку алгоритм потребує O(n2)[3] часу, де n — кількість біт у більшому з двох чисел. Хоча кожен крок зменшує хоча б одне число принаймні вдвічі, для дуже великих чисел віднімання та зсув потребують лінійного часу (втім, на практиці вони доволі швидкі).
Розширений двійковий алгоритм обчислення НСД, аналогічний до розширеного алгоритму Евкліда, описав Дональд Кнут у другому томі «Мистецтва програмування».[4][5]
Реалізація схожа на опис алгоритму зверху. Усі рекурсивні виклики (крім одного) є хвостовою рекурсією.
unsigned int gcd(unsigned int u, unsigned int v)
{
// прості випадки (завершення)
if (u == v)
return u;
if (u == 0)
return v;
if (v == 0)
return u;
// обчислення кількості двійок
if (~u & 1) // u - парне
{
if (v & 1) // v - непарне
return gcd(u >> 1, v);
else // v - парне
return gcd(u >> 1, v >> 1) << 1;
}
if (~v & 1) // u - непарне, v - парне
return gcd(u, v >> 1);
// зменшення більшого аргументу
if (u > v)
return gcd((u - v) >> 1, v);
return gcd((v - u) >> 1, u);
}
Ітеративна реалізація спочатку позбувається спільного дільника 2 застосовуючи рівність 2, потім обчислює НСД, застосовуючи рівності 3 і 4.
unsigned int gcd(unsigned int u, unsigned int v)
{
int shift;
/* НСД(0,v) == v; НСД(u,0) == u, НСД(0,0) == 0 */
if (u == 0) return v;
if (v == 0) return u;
/* Нехай shift := lg K, де K — найбільша степінь двійки, що ділить u і v */
for (shift = 0; ((u | v) & 1) == 0; ++shift) {
u >>= 1;
v >>= 1;
}
while ((u & 1) == 0)
u >>= 1;
/* Починаючи звідси, u завжди непарне. */
do {
/* позбудемось всіх дільників 2 в v -- вони не спільні */
/* зауваження: v не 0, тож цикл завершиться */
while ((v & 1) == 0) /* Loop X */
v >>= 1;
/* Тепер u і v - непарні. Якщо потрібно обміняємо їх, щоб u <= v,
тоді встановимо v = v - u (парне число). Для довгих чисел
обмін - всього переміщення вказівників, і віднімання
можна зробити на місці */
if (u > v) {
unsigned int t = v; v = u; u = t; // Обмін u і v.
}
v = v - u; // Тут v >= u.
} while (v != 0);
/* Відновлюємо спільні дільники 2 */
return u << shift;
}
Доведено, що в теорії, двійковий алгоритм обчислення НСД в середньому на 60 % ефективніший, ніж алгоритм Евкліда (у термінах кількості бітових операцій).[6][7][8] Однак, хоч на практиці цей алгоритм дещо перевершує звичайний алгоритм Евкліда, його асимптотична складність така ж сама, а реалізація непомірно складніша, особливо враховуючи загальнодоступність інструкції цілочисельного ділення на всіх сучасних мікропроцесорах.[9][10]
Справжні комп'ютери оперують із кількома бітами одночасно, тому навіть реалізації двійкового НСД на асемблері мають конкурувати з апаратними схемами для цілочисельного ділення. На гіпотетичному комп'ютері MIX, розширеному бітовими зсувами та перевірками на парність, Кнут повідомляв про 20 % перевагу двійкового алгоритму над звичайним алгоритмом Евкліда.
Для арифметики довільної точності, ні двійковий алгоритм НСД, ні алгоритм Евкліда не є найшвидшими, оскільки обидва вони потребують квадратичного часу від кількості вхідних біт. Натомість, рекурсивні методи, що комбінують ідеї двійкового алгоритму НСД й алгоритму Шьонхаге — Штрассена для швидкого множення цілих чисел, дозволяють досягнути близького до лінійного часу роботи.[11]
- ↑ Stein, J. (1967), Computational problems associated with Racah algebra, Journal of Computational Physics, 1 (3): 397—405, doi:10.1016/0021-9991(67)90047-2, ISSN 0021-9991
- ↑ Knuth, Donald (1998), Seminumerical Algorithms, The Art of Computer Programming, т. 2 (вид. 3rd), Addison-Wesley, ISBN 0-201-89684-2
- ↑ Архівована копія. Архів оригіналу за 5 листопада 2018. Процитовано 4 листопада 2018.
{{cite web}}: Обслуговування CS1: Сторінки з текстом «archived copy» як значення параметру title (посилання) - ↑ Knuth, 1998, с. 646, answer to exercise 39 of section 4.5.2
- ↑ Handbook of Applied Cryptography (PDF). Архів оригіналу (PDF) за 2 лютого 2019. Процитовано 9 вересня 2017.
- ↑ Akhavi, Ali; Vallee, Brigitte (2000), AverageBit-Complexity of Euclidean Algorithms, Proceedings ICALP'00, Lecture Notes Computer Science 1853: 373—387, CiteSeerX: 10.1.1.42.7616, архів оригіналу за 2 жовтня 2006
{{citation}}: Cite має пустий невідомий параметр:|df=(довідка) - ↑ Brent, Richard P. (2000), Twenty years' analysis of the Binary Euclidean Algorithm, Millenial Perspectives in Computer Science: Proceedings of the 1999 Oxford-Microsoft Symposium in honour of Professor Sir Antony Hoare, Palgrave, NY: 41—53, архів оригіналу за 15 квітня 2012, процитовано 4 листопада 2018 proceedings edited by J. Davies, A. W. Roscoe and J. Woodcock.
- ↑ Notes on Programming [Архівовано 25 листопада 2018 у Wayback Machine.] by Alexander Stepanov
- ↑ Jon Stokes (2007). Inside the Machine: An Illustrated Introduction to Microprocessors and Computer Architecture. No Starch Press. с. 117. ISBN 978-1-59327-104-6. Архів оригіналу за 28 червня 2014. Процитовано 4 листопада 2018.
- ↑ Robert Reese; J. W. Bruce; Bryan A. Jones (2009). Microcontrollers: From Assembly Language to C Using the PIC24 Family. Cengage Learning. с. 217. ISBN 1-58450-633-4. Архів оригіналу за 28 червня 2014. Процитовано 4 листопада 2018.
- ↑ Stehle, Damien; Zimmermann, Paul (2004), A binary recursive gcd algorithm, Algorithmic number theory (PDF), Lecture Notes in Comput. Sci., т. 3076, Springer, Berlin, с. 411—425, doi:10.1007/978-3-540-24847-7_31, MR 2138011, архів оригіналу (PDF) за 13 вересня 2014, процитовано 4 листопада 2018.
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Problem 31-1, pg.902.
- NIST Dictionary of Algorithms and Data Structures: binary GCD algorithm [Архівовано 13 жовтня 2018 у Wayback Machine.]
- Cut-the-Knot: Binary Euclid's Algorithm [Архівовано 13 жовтня 2018 у Wayback Machine.] на cut-the-knot
- Analysis of the Binary Euclidean Algorithm [Архівовано 21 березня 2012 у Wayback Machine.] (1976), стаття Richard Brent, включає варіант з використанням зсувів вліво
- «Dynamics of the Binary Euclidean Algorithm: Functional Analysis and Operators» (1998), стаття Brigitte Vallee.
