Реберний граф
В теорії графів реберним графом L(G) неорієнтованого графа G називається граф L(G), що представляє сусідство ребер графа G.
Поняття реберного графа для цього графа настільки звісно, що незалежно було введено багатьма авторами. Звичайно, кожний з них давав свою назву: Оре[1] назвав цей граф «графом, що суміжний», Сабідуссі[2] — «графом похідної», Байнеке [3] — «похідним графом», Сешу і Рід[4] — «реберно-вершинно-двоїстим», Кастелейн[5] — «графом, що покриває», Менон[6] — «приєднаним» («пов'язаним»)[7][8][9].
Одна з найперших та найважливіших теорем про реберні графи належить Вітні, який довів, що за одним винятком, структура графа G повністю визначається реберним графом. Іншими словами, за одним винятком, весь граф може бути відновлений з реберного графа.
Нехай заданий граф G, тоді його реберний граф L(G) — це такий граф, що
- будь-яка вершина графа L(G) являє ребро графа G.
- дві вершини графа L(G) суміжні тоді й лише тоді, коли їх відповідні ребра мають загальну вершину («суміжні») в G.
Такий малюнок показує граф (ліворуч, з синіми вершинами) і його реберний граф (праворуч, із зеленими вершинами). Кожна вершина реберного графа позначена парою номерів - вершин відповідного ребра у вихідному графі. Наприклад, зелена вершина праворуч з міткою 1,3 відповідає ребру ліворуч між блакитними вершинами 1 і 3. Зелена вершина 1,3 суміжна трьом іншим зеленим вершинам: 1,4, 1,2 (відповідної ребрам із загальною вершиною 1 в синьому графі) і 4,3 (відповідної ребрам із загальною вершиною 3 в синьому графі).
-
Граф G
-
Вершини L (G), створені з ребер графа G
-
Додані ребра в L (G)
-
Реберний граф L (G)
Реберний граф повного графа Kn відомий як хордальний граф (або тріангульований граф). Важливою теоремою про хордальні графи є теорема, яка стверджує, що хордальний граф характеризується спектром, за винятком n= 8, коли є три інші графи з тим же спектром, що й у L(K 8). Винятки пояснені в перемиканні графів.
Джерело прикладів реберних графів можна знайти в геометрії — для графів простих багатогранників. Якщо побудувати реберний граф для графа тетраедра отримаємо граф октаедра. З графа куба отримаємо граф кубооктаедра. З графа додекаедра отримаємо граф ікосододекаедра, і т. д. Геометрично операція полягає у відсіканні всіх вершин багатогранника площиною, що перетинає всі ребра, пов'язані з вершиною, в їх середині.
Якщо багатогранник не простий (тобто має понад три грані на вершину), реберний граф НЕ БУДЕ плоским.
Серединний граф — це варіант реберного графа для плоского графа. У серединному графі дві вершини суміжні в тому, і лише в тому випадку, коли відповідні ребра вихідного графа є двома послідовними ребрами деякої області плоского графа. Для простих багатокутників серединний і реберний граф збігаються, але для складних багатокутників серединний граф залишається плоским. Так, серединні графи куба і восьмигранника ізоморфні графа кубооктаедра, а серединні графи дванадцятигранника й ікосаедра ізоморфні графа ікосододекаедра.
Властивості графа G, залежні лише від суміжності ребер, можуть бути переведені в еквівалентні властивості графа L(G), залежні лише від суміжності вершин. Наприклад, парування в G — це множина дуг, жодна з яких не суміжна з іншою, та відповідна множина вершин в L(G), жодна з яких не суміжна з іншою, тобто, незалежна множина вершин.
Отже,
- реберний граф зв'язного графа зв'язний. Якщо G зв'язний, він містить шлях, що з'єднує будь-які два його ребра, який перекладається в шлях графа L (G), що містить будь-які дві вершини графа L(G). Тим не менш, графа G, який містить ізольовані вершини, а тому незв'язні, може відповідати зв'язний реберний граф.
- завдання про максимальну незалежну множину для реберного графа відповідає завданню знаходження максимального парування у вихідному графі.
Оскільки максимальне парування може бути знайдено за поліноміальний час, то й максимальна незалежна множина реберного графа може бути знайдена за поліноміальний час всупереч труднощам пошуку такої множини для більш загальних сімейств графів.
- реберне хроматичне число графа G дорівнює вершинному хроматичному числу його реберного графа L(G).
- реберний граф реберно-транзитивного графа є вершинно-транзитивним графом.
- якщо граф G має Ейлерів цикл, тобто G зв'язаний і має парне число ребер у кожній вершині, то його реберний граф є гамільтоновим графом. (Проте не всі Гамільтонові цикли в реберному графі виходять з Ейлерових циклів.)
- реберний граф не має клешень, тобто породжених підграфів у вигляді трьох листків.
- реберний граф дерева є блоковим графом без клешень.

Граф G є реберним графом якого-небудь іншого графа в тому й лише в тому випадку, коли можна знайти набір клік в G, які розбивають дуги графа G так, що кожна вершина G належить в точності двом клікам. Може статись, що для досягнення цього буде потрібно окремі вершини виділити в кліки. За теоремою Вітні[10][11], якщо G не є трикутником, може бути лише одне розбиття такого роду. Якщо розбиття існує, ми можемо побудувати граф, для якого G буде реберним графом шляхом створення вершини для кожної кліки та з'єднанням отриманих вершин ребром, якщо вершина належить обом клікам. Таким чином, за винятком та , якщо два реберних графи зв'язаних графів ізоморфні, то і графи ізоморфні. Руссопоулос[12] використовував це спостереження, як базис для лінійного за часом алгоритму розпізнавання реберних графів та реконструкції їх вихідних графів.
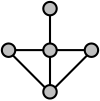
Наприклад, така характеристика може бути використана, щоб показати, що такий граф не є реберним:
У цьому прикладі ребра, що йдуть від центральної вершини 4-о ступеня вгору, вліво та вправо не містять загальних клік. Так, що будь-яке розбиття ребер графа на кліки повинно містити щонайменше одну кліку для кожного з цих трьох ребер, і всі три кліки перетинаються в центральній вершині, що порушує умову, щоб кожна вершина належала в точності двом клікам. Таким чином, показаний граф не може бути реберним графом.
Інша характеристика графа була доведена Байнеке[13] (і була згадана без доведення раніше ним же[3]). Він показав, що є дев'ять мінімальних графів, які не є реберними, таких, що будь-який граф, що не є реберним, містить один з цих дев'яти графів як породжений підграф. Таким чином, граф є реберним тоді і лише тоді, коли ніяка підмножина вершин не породжує один з цих дев'яти. У прикладі, наведеному вище, чотири верхніх вершини породжують клішню (тобто, повний двочастковий граф K 1,3), показаний вгорі ліворуч ілюстрації заборонених підграфів. Таким чином, за характеристикою Байнеке, цей граф не може бути реберним. Для графів зі ступенем вершин не менше 5 лише шість підграфів в лівому та правому стовпчиках малюнка можуть породжуватися графом[14]. Цей результат схожий на результат для реберних графів гіперграфа.[15]
Руідж та Вільф[16] розглянули послідовність графів
Вони показали, що для скінченного зв'язного графа можливі лише чотири види поведінки цієї послідовності:
- Якщо — циклічний граф, то і всі такі ізоморфні самому графу . Це єдине сімейство зв'язних графів, для яких ізоморфно .
- Якщо — клішня , то і всі такі графи є трикутниками.
- Якщо — шлях, то кожний такий реберний граф — скорочений шлях, поки він не перетвориться в порожній граф.
- У всіх інших випадках розмір графів збільшується необмежено.
Якщо незв'язний, то ця класифікація застосована до кожної окремої компоненти зв'язності графа .
Будь-який реберний граф не містить клешень. Реберний граф двочасткового графа є досконалим (дивись теорему Кеніга). Реберні графи двочасткових графів створюють один з ключових блоків, який використовується для доведення теореми про досконалі графи. Спеціальним випадком є турові графи, реберні графи повних двочасткових графів.
Концепція реберного графа для графа G може бути природним чином поширена на випадок, коли G є мультиграфом, хоча в цьому випадку теорема Вітні про єдиність стає невірною. Наприклад, повний двочастковий графK1,n має той самий реберний граф, що й дипольний граф і мультиграф Шеннона з тим же числом ребер.
Можна також узагальнити реберні графи для орієнтованих графів.[17]. Якщо G — орієнтований граф, то його орієнтований реберний граф або реберний орграф має одну вершину для кожної дуги з G. Дві вершини, відповідні дугам з u в v і з w в x з графа G пов'язані дугою з u v в w x в реберному орграфі, коли v=w. Таким чином, кожна дуга в реберному орграфі відповідає шляху довжиною 2 у вихідному графі. Графи де Брёйна можуть бути отримані шляхом багаторазової побудови орієнтованих реберних графів, починаючи з повного орграфа[18].
Кожній вершині ступеня k у вихідному графі G створює k (k-1)/2 ребер у реберному графі L (G). Для багатьох видів аналізу це означає, що вершини високих ступенів уG представлені сильніше в реберному графі L (G). Уявімо, наприклад, випадкове блукання по вершинах вихідного графа G. По ребру e ми пройдемо з деякою ймовірністю f. З іншого боку, ребро e відповідає єдиній вершині, наприклад v, в реберному графі L (G). Якщо ми тепер здійснимо той же самий тип випадкового блукання по вершинах ребрового графа, частота відвідування v може виявитися зовсім відмінною від f. Якщо наше ребро e в G було пов'язане з вершинами ступеня O (k) , воно буде пройдено в O(k2) частіше в реберному графі L (G). Таким чином, хоча теорема Вітні[10] гарантує, що реберний граф майже завжди містить у собі закодовану топологію графа G, це не гарантує, що ці два графи мають прості динамічні зв'язки. Одне з рішень цієї проблеми — створити зважений реберний граф, тобто, реберний граф, у якого ребра забезпечені вагою. Є декілька природних шляхів зробити це[19]. Наприклад, якщо ребра d і e в графі G сполучені в вершині v, що має ступінь k, то в реберному графі L (G) ребру, що з'єднує дві вершини d і e можна приписати вагу 1/ (k-1) . Таким самим чином будь-яке ребро графа G (якщо лише воно не пов'язане з вершиною ступеня '1') матиме вагу 2 в реберному графі L (G), що відповідає двом кінцям ребра в G.
Ребра гіперграфа можуть формувати будь-які сімейства множин, так що реберний граф гіперграфа — це те ж саме, що й граф перетинів множин сімейства.
- ↑ Ore O. Hamilton connected graphs // J. Math. Pures Appl. — 1963. — Т. 42. — С. 21-27.
- ↑ Sabidussi G. Graphs with given group and given praph-theoretical properties // Canad. J. Math.. — 1957. — Т. 9. — С. 515-525.
- ↑ а б Beineke L. W. Beiträge zur Graphentheorie. — Leipzig : Teubner, 1968.
- ↑ Сешу С., Рід М. Лінійні графи та ланцюги. — М. : Высшая школа, 1971. — Т. 42. — С. 21-27.
- ↑ Kasteleyn P. W. A soluble self-avoiding walk problem // Physica. — 1968. — Т. 23. — С. 85-89.
- ↑ Menon V. On repeated interchange graphs // Amer Math Monthly. — 1966. — Т. 13. — С. 986-989.
- ↑ Ф. Харарі. Теорія графів = Graph Theory. — 2. — М. : Едиториал УРСС, 2003. — 296 с.
- ↑ Balakrishnan V. K. Schaum's Outline of Graph Theory. — 1st. — McGraw-Hill, 1997. — ISBN 0-07-005489-4.
- ↑ R. L. Hemminger, L. W. Beineke. Selected Topics in Graph Theory. — Academic Press Inc., 1978. — С. 271–305.
- ↑ а б H. Whitney. Congruent graphs and the connectivity of graphs // American Journal of Mathematics. — 1932. — Т. 54, вип. 1. — С. 150–168. — DOI:.
- ↑ J. Krausz. Démonstration nouvelle d'un théorème de Whitney sur les réseaux // Mat. Fiz. Lapok. — 1943. — Т. 50. — С. 75–85..
- ↑ N. D. Roussopoulos. A max {m,n} algorithm for determining the graphHfrom its line graphG // Information Processing Letters. — 1973. — Т. 2. — С. 108–112. — DOI:..
- ↑ L. W. Beineke. Characterizations of derived graphs // Journal of Combinatorial Theory. — 1970. — Т. 9, вип. 2. — С. 129–135. — DOI:.
- ↑ Yury Metelsky, Regina Tyshkevich. On line graphs of linear 3-uniform hypergraphs // Journal of Graph Theory. — 1997. — Т. 25. — С. 243–251. — DOI:..
- ↑ Weisstein, Eric W. Line Graph(англ.) на сайті Wolfram MathWorld.
- ↑ A. C. M. van Rooij, H. S. Wilf. The interchange graph of a finite graph // Acta Mathematica Hungarica. — 1965. — Т. 16. — С. 263–269. — DOI:..
- ↑ Frank Harary, R. Z. Norman. Some properties of line digraphs // Rendiconti del Circolo Matematico di Palermo. — 1960. — Т. 9, вип. 2. — С. 161–169. — DOI:..
- ↑ Fu Ji Zhang, Guo Ning Lin. On the de Bruijn–Good graphs // Acta Math. Sinica. — 1987. — Т. 30, вип. 2. — С. 195–205.
- ↑ T.S. Evans, R. Lambiotte. Line Graphs, Link Partitions and Overlapping Communities // Phys.Rev.E. — 2009. — Т. 80. — DOI:.
- Andreas Brandstädt, Van Bang Le, Jeremy P. Spinrad. Graph Classes: A Survey. — SIAM Monographs on Discrete Mathematics and Applications, 1999. — ISBN 0-89871-432-X..