Локалізація точки
Локалізація точки є однією з фундаментальних задач обчислювальної геометрії. Вона знаходить застосування в галузях, що оперують геометричною інформацією: комп'ютерна графіка, геоінформаційні системи (ГІС), планування руху і системи автоматизованого проектування (САПР).
У найзагальнішому вигляді, завдання полягає в тому, щоб для заданого розбиття простору на області (вони не перетинаються), визначити область, якій належить точка запиту. Приклад застосування: після кожного клацання мишею на екрані монітору, проблема локалізації точки повинна бути вирішена для того, щоб визначити, яка область екрана комп'ютера знаходиться під вказівником миші.
Простим, але важливим випадком є задача про належність точки многокутнику. У цьому випадку, ми повинні визначити, знаходиться точка всередині, зовні чи на межі заданого полігону.
У багатьох застосунках, потрібно визначити місце розташування декількох різних точок відносно одного й того ж розбиття простору. Для ефективного вирішення цієї проблеми корисно створити структуру даних, яка, розрахована на масові запити і швидко визначає, яка область містить точку запиту.

Визначено плаский прямолінійний граф (ППЛГ), який розбиває площину на багатокутні області, та точка z. З'ясувати якій області належить точка z.

Через кожну вершину графу проводимо вертикальну лінію. Таким чином отримуємо вертикальні смуги впорядковані за координатою x. Для кожного ребра, яке перетинає смугу записуємо нове укорочене ребро у впорядкований перелік за координатою y. Пошук відбувається за логарифмічний час з використанням квадратичної пам'яті у найгіршому випадку.

Ідея методу походить від пошуку в прямокутній решітці. Граф розбивається на «вертикальні» та «горизонтальні» смуги. В методі ланцюгів вертикальні смуги замінюються на ланцюги монотонні відносно осі Oy. При запиті відносно розташування точки в ППЛГ, спочатку відбувається бінарний пошук для з'ясування між якими «вертикальними» ланцюгами розташована точка. Такий пошук реалізується за допомогою підпрограми, яка обробляє запит (ланцюг, точка) і дає відповідь на те, як розташована точка відносно ланцюга — ліворуч чи праворуч.
Алгоритм який з'ясовує розташування точки працює за допомогою бінарного пошуку. Тим самим він працює з логарифмічною швидкістю.
У підсумку пошук відбувається за час . Використовується пам'ять .
У 2013 році командою з Київського національного університету імені Тараса Шевченка була запропонована модифікація методу ланцюгів, що дозволяє досягти лінійного використання пам'яті та логарифмічного часу пошуку.[1]
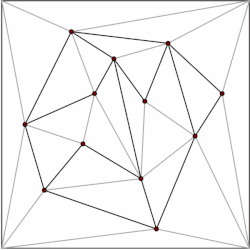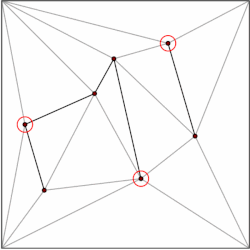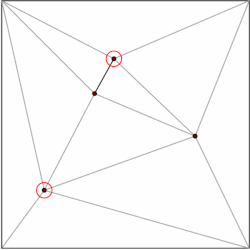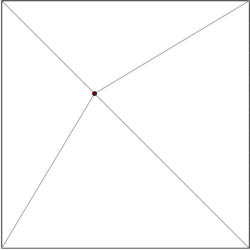
Багатокутник з m вершинами можна розбити на m-2 трикутника. Існують чисельні алгоритми для ефективної триангуляції багатокутника, найшвидший з них працює за час O(n) в найгіршому випадку. Таким чином, ми можемо розкласти кожен багатокутник нашого розбиття на трикутники, і обмежитися структурними даними на випадок розбиттів, сформованих виключно з трикутників. Kirkpatrick описує структуру даних для опису тріангульованого розбиття яка використовує пам'ять O(n) і запити виконуються за час O(log n).
Загальна ідея полягає у створенні ієрархії трикутників. Щоб виконати запит, ми почнемо з знаходження верхнього рівня трикутник, що містить точку запиту. Так як число трикутників верхнього рівня обмежено константою, ця операція може бути виконана за O(1). Кожен трикутник має вказівник на трикутники, які він перетинає в наступному рівні ієрархії, а кількість вказівників також обмежена константою. Переходимо із запитом на знаходження, який трикутник містить вказівник рівня запиту по рівню.
Структура даних побудована в зворотному порядку, тобто знизу вгору. Починаємо з тріангульованих підрозділів і вибираємо незалежний набір вершин, які будуть видалені. Після видалення вершин, ми ретріангулюємо підрозділ. Оскільки підрозділ формується з трикутників, жадібний алгоритм може знайти незалежний набір, що містить постійну частину вершин. Таким чином, кількість кроків видалення становить O(log n).

Увипадковлений підхід до задачі локалізації точки, і, ймовірно, найбільш практичний, заснований на трапецієподібному розкладанні або трапецієподібній карті. Трапецієподібне розкладання отримують, випускаючи вертикальні промені, що йдуть вгору і вниз з кожної вершини у вихідні підрозділи. Промені треба зупинити, коли вони потрапили в край, і сформувати новий край у підрозділі. Таким чином, ми отримаємо підмножину, яка є розкладанням в плиту, тільки з O(n) ребер і вершин, так як ми тільки додати два ребра і дві вершини для кожної вершини в первинному підрозділі.
Однак, це не легко побачити, як використовувати трапецієподібне розкладання для точки розташування, так як бінарний пошук, аналогічний використовуваному в плитковому розкладанні не може бути більше використаний. Замість цього, нам необхідно відповісти на запит у той же спосіб, як у уточненому підході тріангуляції, але структура даних будується зверху вниз. Спочатку ми будуємо трапецієподібне розкладання, яке містить лише рамку, і ніякої внутрішньої вершини. Потім ми додаємо сегменти з підрозділу, один за іншим, у випадковому порядку, уточнення трапецієподібного розкладання. Використання зворотного аналізу, ми можемо показати, що очікуване число трапецій, створених для кожної вставки обмежене константою.
Ми будуємо орієнтований ациклічний граф, в якому вершини є трапеції, які існували в якийсь момент в уточненні, і спрямовані ребра з'єднують трапеції отримані за допомогою підрозділів. Очікується, глибина пошуку в цьому орієнтованому графі, починаючи з вершини, яка відповідає прямокутнику, є O(log n).
- de Berg, Mark; van Kreveld, Marc; Overmars, Mark; Schwarzkopf, Otfried (2000). Chapter 6: Point location. Computational Geometry (вид. 2nd revised). Springer-Verlag. с. 121–146. ISBN 3-540-65620-0.
- Dobkin, David; Lipton, Richard J. (1976). Multidimensional searching problems. SIAM Journal on Computing. 5 (2): 181—186. doi:10.1137/0205015.
- Snoeyink, Jack (2004). Chapter 34: "Point Location. У Goodman, Jacob E.; O'Rourke, Joseph (ред.). Handbook of Discrete and Computational Geometry (вид. 2nd). Chapman & Hall/CRC. ISBN 1-58488-301-4.
- Sarnak, Neil; Tarjan, Robert E. (1986). Planar point location using persistent search trees. Communications of the ACM. 29 (7): 669—679. doi:10.1145/6138.6151.
- Edelsbrunner, Herbert; Guibas, Leonidas J.; Stolfi, Jorge (1986). Optimal point location in a monotone subdivision. SIAM Journal on Computing. 15 (2): 317—340. doi:10.1137/0215023.
- Kirkpatrick, David G. (1983). Optimal search in planar subdivisions. SIAM Journal on Computing. 12 (1): 28—35. CiteSeerX 10.1.1.461.1866. doi:10.1137/0212002.
- Терещенко, В.М., 2013. Модифікація методу ланцюгів для задачі локалізації точки. Вісник Київського національного університету імені Тараса Шевченка. Серія: Фізико-математичні науки, (2), pp.233-236.
- Point-Location Source Repository [Архівовано 23 липня 2014 у Wayback Machine.] в університеті у Стоуні-Брук
- Point-Location Queries [Архівовано 23 червня 2013 у Wayback Machine.] в CGAL[en] — Computational Geometry Algorithms Library
- Препарата Ф., Шеймос М. Вычислительная геометрия. Введение. Раздел 2.2.2: М.: Мир, 1989.
| Це незавершена стаття з геометрії. Ви можете допомогти проєкту, виправивши або дописавши її. |


