Фільтр високих частот
Фільтр верхніх частот (ФВЧ) — це електронний фільтр, що пропускає високочастотні сигнали, але послаблює (зменшує амплітуду) сигналів з частотами нижче частоти зрізу. Фактична величина ослаблення для кожної частоти варіюється у різних фільтрів. Фільтр верхніх частот зазвичай моделюється як лінійна стаціонарна система. Високочастотні фільтри мають безліч застосувань, таких як блокування постійного струму від електричної схеми чутливої до ненульової середньої напруги або радіочастотного пристрою. Вони також можуть бути використані разом із фільтром нижніх частот, для побудови смугового фільтру.
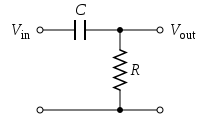
Простий електронний фільтр високих частот першого порядку, що на Рис. 1 реалізується шляхом під'єднання вхідної напруги до послідовно з'єднаних резистора та конденсатора і з використанням напруги на резисторі як вихідного сигналу. Результат добутку значень опору та ємності (R×C) є часова константа (τ); вона обернено пропорційна частоті зрізу fc, тобто:
де fc вимірюється в герцах, τ — в секундах, R — в Омах, а C — в Фарадах.
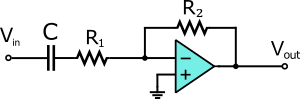
На рис. 2 показана електронна реалізація активного високочастотного фільтру першого порядку з використанням операційного підсилювача. У цьому випадку фільтр має кутову частоту
Оскільки цей фільтр активний, він може мати не єдиний коефіцієнт підсилення. Це означає, що високочастотні сигнали інвертуються і посилюється в R2/R1.
Дискретні за часом високочастотні фільтри також можуть бути розроблені. Простий приклад побудови дискретного у часі фільтра можна отримати при перетворенні фільтра безперервного у часі. Тобто, при розгляді безперервного часу поведінка може бути дискретною.
Зі схеми на рис. 1 вище, відповідно до законів Кірхгофа та визначення ємності:
де — заряд, накопичений в конденсаторі в певний момент часу . Після підстановки рівняння (Q) в рівняння (I) а потім рівняння (I) в рівняння (V) отримуємо:
Це рівняння може бути дискретним. Для простоти припустимо, що зразки вхідних і вихідних приймаються на рівномірно розташованих моментів часу розділених в . Нехай зразки будуть представлені послідовністю , а будуть представлені послідовністю які відповідають однаковим моментам часу. Внесення цих замін дає:
Перестановки членів дають рекурентне співвідношення
Тобто, цей дискретний за часом реалізації простий безперервний у часі RC-фільтр високих частот визначається
За визначенням, . Вираз для параметра дає еквівалентна стала часу в термінах періоду дискретизації , а також :
Якщо , то стала дорівнює періоду дискретизації. Якщо , таким чином, значно менше інтервалу дискретизації, і .
Фільтр рекурентного співвідношення надає спосіб визначення вихідних вибірок з точки зору вхідних вибірок і попереднього виходу. Наступний псевдокод буде імітувати ефект фільтра високих частот на серії цифрових вибірок:
// Повертає RC-фільтр високих частот вихідних вибірок, з урахуванням вхідних вибірок,
// Інтервал часу dt, і постійна часу RC
function highpass(real[0..n] x, real dt, real RC)
var real[0..n] y
var real α := RC / (RC + dt)
y[0] := x[0]
for i from 1 to n
y[i] := α * y[i-1] + α * (x[i] - x[i-1])
return y
Цикл, який обчислює кожен з виходів, може бути представлений еквівалентно:
for i from 1 to n
y[i] := α * (y[i-1] + x[i] - x[i-1])
Проте попередня форма показує, як параметр α змінює вплив попереднього вихідного сигналу y[i-1], а струм змінюється на вході (x[i] - x[i-1]). Зокрема,
- Якщо значення α велике, то на виході сигнал буде затухати дуже повільно, але сильно залежним навіть від невеликих змін на вході. Внаслідок зв'язку між α і параметром постійної часу , велике α відповідає великому і, отже, низькій циклічній частоті фільтра. Таким чином, цей випадок відповідає фільтру високих частот з дуже вузькою смугою затримування. Так як вона збуджує невеликі зміни і прагне зробити внесок у вихідні значення протягом тривалого часу, вона може відбуватися при відносно низьких частотах. Тим не менш, при подачі сталого вхідного сигналу (тобто на вході (x[i] - x[i-1])=0) завжди буде відбуватись затухання до нуля, як і слід було очікувати з фільтра верхніх частот з великим значенням .
- Невелике α означає, що на виході сигнал буде падати швидше і спричинить те, що великі зміни на вході (тобто (x[i] - x[i-1]) має велике значення) викликатимуть значні зміни на виході. Внаслідок зв'язку між α і параметром постійної часу , невелике α відповідає невеликим і, отже, високій циклічній частоті фільтра. Таким чином, цей випадок відповідає фільтру високих частот з дуже широкою смугою затримування.
Фільтри верхніх частот мають багато застосувань. Вони використовуються як частина аудіо кросовера, направляють високі частоти до твітера, в той же час ослаблюють низькочастотні сигнали, які можуть заважати або пошкодити динамік. Зазвичай в корпус гучномовця вбудовують звичайний пасивний фільтр, який включає в себе фільтр низьких частот для репродукції низьких тонів, часто використовують конденсатор і котушку індуктивності (хоча дуже простий фільтр високих частот для твітерів/ динаміків може містити тільки серійний конденсатор і більше нічого). Як приклад, за наведеною вище формулою, застосованою до твітера з опором R = 10 Ом, можна визначити ємність конденсатора для частоти зрізу 5 кГц. , або приблизно 3.2 мкФ.
Альтернативою, що забезпечує гарну якість звуку без індукторів (які схильні до паразитного зв'язку, дорогі, і можуть мати значний внутрішній опір), є використання подвійного підсилення активним RC-фільтром або активним цифровим фільтром з окремих підсилювачів потужності для кожного гучномовця. Такі слабкострумові і низьковольтні кросовери лінійного рівня, називаються активними кросоверами.
Фільтр гуркіту — це фільтр верхніх частот, що застосовується для видалення небажаних звуків поруч з нижнім кінцем чутного діапазону або нижче. Наприклад, шум (кроки чи моторні шуми програвачів та магнітофонів) можуть бути видалені, оскільки вони є небажаними або можуть призвести до перевантаження RIAA компенсації ланцюга попереднього підсилювача.
Високочастотні фільтри також використовуються для змінного струму на входах багатьох аудіо-підсилювачів потужності для запобігання посилення постійного струму, який може завдати шкоди підсилювачу і генерувати тепло на звуковій котушці гучномовця. Один підсилювач, професійна аудіо модель DC300 розроблена Crown International, починаючи з 1960-х років, не мав високочастотної фільтрації взагалі, і міг бути використаний для посилення сигналу постійного струму звичайної 9-вольтової батареї на вході джерела 18 вольт DC в надзвичайній ситуації для змішування потужності корпуса приймача. Тим не менш, базова конструкція моделі була замінена на новішу, таку як Crown Macro-Tech серії, що розроблена наприкінці 1980-х років, яка включала 10 Гц фільтрації верхніх частот на входах і перемикання на 35 Гц високочастотної фільтрації на виходах. Іншим прикладом є QSC Audio підсилювач PLX серії, який включає в себе внутрішній на 5 Гц фільтр високих частот, який застосовується до вхідних сигналів, коли додаткові 50 і 30 Гц ВЧ фільтри вимкнені.

Мікшерні пульти часто включають в себе високочастотну фільтрацію на кожному каналі. Деякі моделі мають фіксоване зменшення, з фіксованою частотою високочастотних фільтрів при 80 або 100 Гц, які можуть бути задіяні, інші моделі мають регульовані 'обрізні ФВЧ'-фільтр високих частот основного зменшення, яке може бути встановлене в межах вказаного діапазону частот, наприклад, від 20 до 400 Гц на Midas Heritage 3000, або від 20 до 20 000 Гц на Yamaha M7CL. Ветеран інженерних систем і живий звуковий мікшер Брюс Мейн рекомендує, щоб високочастотні фільтри були задіяні для більшості вхідних джерел мікшера, за винятком таких, як бас-гітара і фортепіано, які матимуть низькочастотні звуки. Мейн пише, що DI блоку входів (на відміну від мікрофонних входів) не потрібна фільтрація верхніх частот, оскільки вони не підлягають модуляції низькочастотної стадії фільтрування низькочастотних звуків, які виходять з сабвуферів або системи оповіщення. Мейн вказує, що високочастотні фільтри зазвичай використовуються для спрямованих мікрофонів, які мають ефект наближення — низькочастотний імпульс для дуже близьких джерел. Цей низькочастотний імпульс зазвичай викликає проблеми вище 200 або 300 Гц, але Мейн зазначає, що є мікрофони, які мають від 500 Гц ФВЧ налаштованих на консолі.

Фільтри високих і низьких частот також використовуються в цифровій обробці зображень для модифікації, доповнення, зменшення шуму і т. д., з використанням зображень зроблених в будь-якій просторовій або в частотній області.
Фільтр високих частот, якщо графічне програмне забезпечення не має жодного, може бути зроблено шляхом дублювання шару, розмиття по Гаусу, інвертування, а потім об'єднання з оригінальним шаром з непрозорістю (скажімо, 50 %) із початковим шаром.
Операція нерізкого маскування, яка використовується в програмному забезпеченні для редагування зображень, — є високоімпульсним фільтром, узагальненням фільтра високих частот.
- Фільтр низьких частот
- Електронний фільтр
- Смуговий фільтр
- Режекторний фільтр
- Фазовий фільтр
- Фільтрація звуку
- Хоровиц П., Хилл У. Искусство схемотехники (в 2-х томах) = The Art of Electronics. — М.: Мир, 1980. — Т. 2. — 590 с. (рос.)























