Файл:VFPt metal balls largesmall potential.svg

Повна роздільність (SVG-файл, номінально 800 × 600 пікселів, розмір файлу: 156 КБ)
| Відомості про цей файл містяться на Вікісховищі — централізованому сховищі вільних файлів мультимедіа для використання в проектах Фонду Вікімедіа. |
Опис файлу
| ОписVFPt metal balls largesmall potential.svg |
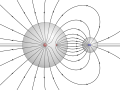
English: Electric field around a large and a small conducting sphere at opposite electric potential. The shape of the field lines is computed exactly, using the method of image charges with an infinite series of charges inside the two spheres. Field lines are always orthogonal to the surface of each sphere. In reality, the field is created by a continuous charge distribution at the surface of each sphere, indicated by small plus and minus signs. The electric potential is depicted as background color with yellow at 0V. |
||
| Час створення | |||
| Джерело | Власна робота | ||
| Автор | Geek3 | ||
| Інші версії |
|
||
| SVG розвиток InfoField | Вихідний код цього SVG-файлу неправильний. Це векторне зображення було створено з допомогою Inkscape, or with something else.
| ||
| Сирцевий код InfoField | SVG code# paste this code at the end of VectorFieldPlot 1.10
# https://commons.wikimedia.org/wiki/User:Geek3/VectorFieldPlot
u = 100.0
doc = FieldplotDocument('VFPt_metal_balls_largesmall_potential',
commons=True, width=800, height=600, center=[400, 300], unit=u)
# define two spheres with position, radius and charge
s1 = {'p':sc.array([-1.0, 0.]), 'r':1.5}
s2 = {'p':sc.array([2.0, 0.]), 'r':0.5}
# make charge proportional to capacitance, which is proportional to radius.
s1['q'] = s1['r']
s2['q'] = -s2['r']
d = vabs(s2['p'] - s1['p'])
v12 = (s2['p'] - s1['p']) / d
# compute series of charges https://dx.doi.org/10.2174/1874183500902010032
charges = [[s1['p'][0], s1['p'][1], s1['q']], [s2['p'][0], s2['p'][1], s2['q']]]
r1 = r2 = 0.
q1, q2 = s1['q'], s2['q']
q0 = max(fabs(q1), fabs(q2))
for i in range(10):
q1, q2 = -s1['r'] * q2 / (d - r2), -s2['r'] * q1 / (d - r1),
r1, r2 = s1['r']**2 / (d - r2), s2['r']**2 / (d - r1)
p1, p2 = s1['p'] + r1 * v12, s2['p'] - r2 * v12
charges.append([p1[0], p1[1], q1])
charges.append([p2[0], p2[1], q2])
if max(fabs(q1), fabs(q2)) < 1e-3 * q0:
break
field = Field({'monopoles':charges})
# draw potential in background
p_array = sc.array([c[:2] for c in charges])
q_array = sc.array([c[2] for c in charges])
def potential(xy):
return sc.dot(q_array, 1. / sc.linalg.norm(xy - p_array, axis=1))
from matplotlib import colors
# colormap from aqua through yellow to fuchsia
cmap = colors.ListedColormap([sc.clip((2*x, 2*(1-x), 4*(x-0.5)**2), 0, 1)
for x in sc.linspace(0., 1., 2048)])
doc.draw_scalar_field(func=potential, cmap=cmap,
vmin=potential(s2['p'] + s2['r'] * sc.array([1., 0.])),
vmax=potential(s1['p'] + s1['r'] * sc.array([-1., 0.])))
# draw symbols
for c in charges:
doc.draw_charges(Field({'monopoles':[c]}), scale=0.6*sqrt(fabs(c[2])))
gradr = doc.draw_object('linearGradient', {'id':'rod_shade', 'x1':0, 'x2':0,
'y1':0, 'y2':1, 'gradientUnits':'objectBoundingBox'}, group=doc.defs)
for col, of in (('#666', 0), ('#ddd', 0.6), ('#fff', 0.7), ('#ccc', 0.75),
('#888', 1)):
doc.draw_object('stop', {'offset':of, 'stop-color':col}, group=gradr)
gradb = doc.draw_object('radialGradient', {'id':'metal_spot', 'cx':'0.53',
'cy':'0.54', 'r':'0.55', 'fx':'0.65', 'fy':'0.7',
'gradientUnits':'objectBoundingBox'}, group=doc.defs)
for col, of in (('#fff', 0), ('#e7e7e7', 0.15), ('#ddd', 0.25),
('#aaa', 0.7), ('#888', 0.9), ('#666', 1)):
doc.draw_object('stop', {'offset':of, 'stop-color':col}, group=gradb)
ball_charges = []
for ib in range(2):
ball = doc.draw_object('g', {'id':'metal_ball{:}'.format(ib+1),
'transform':'translate({:.3f},{:.3f})'.format(*([s1, s2][ib]['p'])),
'style':'fill:none; stroke:#000;stroke-linecap:square', 'opacity':1})
# draw rods
if ib == 0:
x1, x2 = -4.1 - s1['p'][0], -0.9 * s1['r']
else:
x1, x2 = 0.9 * s2['r'], 4.1 - s2['p'][0]
doc.draw_object('rect', {'x':x1, 'width':x2-x1,
'y':-0.1/1.2+0.01, 'height':0.2/1.2-0.02,
'style':'fill:url(#rod_shade); stroke-width:0.02'}, group=ball)
# draw metal balls
doc.draw_object('circle', {'cx':0, 'cy':0, 'r':[s1, s2][ib]['r'],
'style':'fill:url(#metal_spot); stroke-width:0.02'}, group=ball)
ball_charges.append(doc.draw_object('g',
{'style':'stroke-width:0.02'}, group=ball))
# find well-distributed start positions of field lines
def get_startpoint_function(startpath, field):
'''
Given a vector function startpath(t), this will return a new
function such that the scalar parameter t in [0,1] progresses
indirectly proportional to the orthogonal field strength.
'''
def dstartpath(t):
return (startpath(t+1e-6) - startpath(t-1e-6)) / 2e-6
def FieldSum(t0, t1):
return ig.quad(lambda t: sc.absolute(sc.cross(
field.F(startpath(t)), dstartpath(t))), t0, t1)[0]
Ftotal = FieldSum(0, 1)
def startpos(s):
t = op.brentq(lambda t: FieldSum(0, t) / Ftotal - s, 0, 1)
return startpath(t)
return startpos
startp = []
def startpath1(t):
phi = 2. * pi * t
return (sc.array(s2['p']) + 1.5 * sc.array([cos(phi), sin(phi)]))
start_func1 = get_startpoint_function(startpath1, field)
nlines1 = 16
for i in range(nlines1):
startp.append(start_func1((0.5 + i) / nlines1))
def startpath2(t):
phi = 2. * pi * (0.195 + 0.61 * t)
return (sc.array(s1['p']) + 1.5 * sc.array([cos(phi), -sin(phi)]))
start_func2 = get_startpoint_function(startpath2, field)
nlines2 = 14
for i in range(nlines2):
startp.append(start_func2((0.5 + i) / nlines2))
# draw the field lines
for p0 in startp:
line = FieldLine(field, p0, directions='both', maxr=7.)
# draw little charge signs near the surface
path_minus = 'M {0:.5f},0 h {1:.5f}'.format(-2./u, 4./u)
path_plus = 'M {0:.5f},0 h {1:.5f} M 0,{0:.5f} v {1:.5f}'.format(-2./u, 4./u)
for si in range(2):
sphere = [s1, s2][si]
# check if fieldline ends inside the sphere
for ci in range(2):
if vabs(line.get_position(ci) - sphere['p']) < sphere['r']:
# find the point where the field line cuts the surface
t = op.brentq(lambda t: vabs(line.get_position(t)
- sphere['p']) - sphere['r'], 0., 1.)
pr = line.get_position(t) - sphere['p']
cpos = 0.9 * sphere['r'] * pr / vabs(pr)
doc.draw_object('path', {'stroke':'black', 'd':
[path_plus, path_minus][ci],
'transform':'translate({:.5f},{:.5f})'.format(
round(u*cpos[0])/u, round(u*cpos[1])/u)},
group=ball_charges[si])
arrow_d = 2.0
of = [0.5 + s1['r'] / arrow_d, 0.5, 0.5, 0.5 + s2['r'] / arrow_d]
doc.draw_line(line, arrows_style={'dist':arrow_d, 'offsets':of})
doc.write()
|
Ліцензування
- Ви можете вільно:
- ділитися – копіювати, поширювати і передавати твір
- модифікувати – переробляти твір
- При дотриманні таких умов:
- зазначення авторства – Ви повинні вказати авторство, надати посилання на ліцензію і вказати, чи якісь зміни було внесено до оригінального твору. Ви можете зробити це в будь-який розсудливий спосіб, але так, щоб він жодним чином не натякав на те, наче ліцензіар підтримує Вас чи Ваш спосіб використання твору.
- поширення на тих же умовах – Якщо ви змінюєте, перетворюєте або створюєте іншу похідну роботу на основі цього твору, ви можете поширювати отриманий у результаті твір тільки на умовах такої ж або сумісної ліцензії.
Підписи
Об'єкти, показані на цьому файлі
зображує
Якесь значення без елемента на сайті Вікідані
30 грудня 2018
image/svg+xml
Історія файлу
Клацніть на дату/час, щоб переглянути, як тоді виглядав файл.
| Дата/час | Мініатюра | Розмір об'єкта | Користувач | Коментар | |
|---|---|---|---|---|---|
| поточний | 20:05, 30 грудня 2018 |  | 800 × 600 (156 КБ) | Geek3 | User created page with UploadWizard |
Використання файлу
Така сторінка використовує цей файл:
Глобальне використання файлу
Цей файл використовують такі інші вікі:
- Використання в af.wikipedia.org
- Використання в ar.wikipedia.org
- Використання в ast.wikipedia.org
- Використання в be.wikipedia.org
- Використання в ca.wikipedia.org
- Використання в eu.wikipedia.org
- Використання в ga.wikipedia.org
- Використання в ko.wikipedia.org
- Використання в www.wikidata.org
Метадані
Файл містить додаткові дані, які зазвичай додаються цифровими камерами чи сканерами. Якщо файл редагувався після створення, то деякі параметри можуть не відповідати цьому зображенню.
| Коротка назва | VFPt_metal_balls_largesmall_potential |
|---|---|
| Назва зображення | VFPt_metal_balls_largesmall_potential
created with VectorFieldPlot 1.10 https://commons.wikimedia.org/wiki/User:Geek3/VectorFieldPlot about: https://commons.wikimedia.org/wiki/File:VFPt_metal_balls_largesmall_potential.svg rights: Creative Commons Attribution ShareAlike 4.0 |
| Ширина | 800 |
| Висота | 600 |