Відображення Хенона

Відображення Хенона при a=1,4 та b=0,3

Атрактор Хенона при a=1,4 та b=0,3

Відображення Хенона (Відображення Енона, англ. Hénon map) є дискретною в часі динамічною системою. Це один з найбільш вивчених прикладів динамічних систем, які проявляють хаотичну поведінку. Відображення Хенона займає точку (x_n, y_n) в площині і зіставляє його до нової точки

$x_{n+1}=1-ax_{n}^{2}+y_{n}\,$

$y_{n+1}=bx_{n}\,$

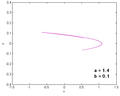
Відображення залежить від двох параметрів, a та b, які для класичного відображення Хенона мають значення a = 1,4 та b = 0,3. Для класичних значень відображення Хенона є хаотичним. При інших значеннях a та b відображення може бути хаотичним, з перервами чи сходитися до періодичної орбіти. Огляд типу поведінки відображення при різних значеннях параметрів можуть бути отримані зі схеми його орбіти.

Відображення було введене Мішелем Хеноном як спрощена модель перетину Пуанкаре моделі Лоренца. Для класичного відображення, початкова точка площини повинна наближатися до набору точок, відомих як дивний атрактор Хенона, або прямувати до нескінченності. Атрактор Хенона є фракталом, гладким в одному напрямку, а в наборі Кантора іншим. Чисельні оцінки кореляції в околі 1,25 ± 0,02 і в розмірності Гаусдорфа 1,261 ± 0,003 для атрактора класичного відображення.

Атрактор

Орбіта діаграми відображення Хенона з b=0,3. Більш висока щільність (темніше на малюнку) вказує на посилення ймовірності змінної x набуває цього значення для поданого значення a. Зверніть увагу на супутникові регіони хаосу і періодичність навколо a=1,075 -- вони можуть виникнути в залежності від початкових умов для x та y.

Відображення Хенона відображує дві точки самі в себе: це інваріантні точки. Для класичних значень a та b відображення Хенона, одна з цих точок знаходиться на атракторі:

$x={\frac {{\sqrt {609}}-7}{28}}\approx 0,631354477\dots \qquad y={\frac {3\left({\sqrt {609}}-7\right)}{280}}\approx 0,189406343\dots \,$

Ця точка нестійка. Значення близькі до цієї нерухомої точки і вздовж нахилу 1,924 буде наближати нерухому точку і точки вздовж нахилу -0,156 будуть відходи від фіксованої точки. Ці схили виникають з лінеаризацією сталого різноманіття і нестійкого різноманіття нерухомої точки. Нестійке різноманіття нерухомої точки в атракторі міститься в дивному атракторі відображення Хенона. 

Відображення Хенона не має дивного атрактора для всіх значеннях параметрів a та b. Наприклад, зберігаючи b фікссованим на 0,3 діаграма біфуркації показує, що при a = 1,25 відображення Хенона має стабільну періодичну орбіту як атрактора.

Цвітановіч та ніші показали, як структуру дивного атрактора Хенона можна зрозуміти з точки зору нестійких періодичних орбіт в межах атрактора.

Декомпозиція

Відображення Хенона може бути розкладене на площі, що зберігає вигин:

$(x_{1},y_{1})=(x,1-ax^{2}+y)\,$,

скорочення в напрямку x:

$(x_{2},y_{2})=(bx_{1},y_{1})\,$,

і відображення в прямій y = x:

$(x_{3},y_{3})=(y_{2},x_{2})\,$.

Властивості

Спочатку цей процес виглядає випадковим розміщенням точок на графіку. Тільки після нанесення великої кількості значень проявиться шаблон. Продовжуючи ітерації, точок стає так багато, що вони формують суцільні лінії. Якщо почати збільшувати сформовані лінії, то можна побачити, що окремі лінії складаються з інших ліній. Цю характеристику називають "самоподібністю", вона і є особливістю багатьох фракталів. Дана властивість вимагає виконання нескінченної кількості ітерацій, в інакше рано чи пізно лінії поступово розпадуться на окремі точки.

• 
  Атрактор Хенона (оригінал)
• 
  8-кратне збільшення Атрактора Хенона
• 
  64-кратне збільшення Атрактора Хенона
• 
  512-кратне збільшення Атрактора Хенона

Параметри a та b

Можна змінити значення для a і b, таким чином створивши атрактори, які будуть відрізнятися від оригінального зображення.

Доцільно вносити незначні зміни у невеликому околі значень a та b, бо фрактал має бути схожим на атрактор Хенона.

Нижче наведені приклади інших атракторів Хенона з різними значеннями a та b.

• 
  a=1,2 b=0,3
• 
  a=1,3 b=0,3
• 
  a=1,4 b=0,3
• 
  a=1,4 b=0,1
• 
  a=1,5 b=0,2

Див. також

• Підкова Смейла
• Атрактор Пликіна

Джерела

• M. Hénon (1976). A two-dimensional mapping with a strange attractor. Communications in Mathematical Physics. 50 (1): 69—77. Bibcode:1976CMaPh..50...69H. doi:10.1007/BF01608556.
• Predrag Cvitanović, Gemunu Gunaratne, and Itamar Procaccia (1988). Topological and metric properties of Hénon-type strange attractors. Physical Review A. 38 (3): 1503—1520. Bibcode:1988PhRvA..38.1503C. doi:10.1103/PhysRevA.38.1503. PMID 9900529.
• M. Michelitsch and O. E. Rössler (1989). A New Feature in Hénon's Map. Computers & Graphics. 13 (2): 263—265. doi:10.1016/0097-8493(89)90070-8. Архів оригіналу за 25 січня 2021. Процитовано 28 березня 2014.. Reprinted in: Chaos and Fractals, A Computer Graphical Journey: Ten Year Compilation of Advanced Research (Ed. C. A. Pickover). Amsterdam, Netherlands: Elsevier, pp. 69–71, 1998

Посилання

• Interactive Henon map [Архівовано 28 березня 2014 у Wayback Machine.] and Henon attractor [Архівовано 28 лютого 2014 у Wayback Machine.] in Chaotic Maps [Архівовано 28 березня 2014 у Wayback Machine.]
• Another interactive iteration of the Henon Map [Архівовано 13 червня 2011 у Wayback Machine.] by A. Luhn
• Orbit Diagram of the Hénon Map [Архівовано 28 березня 2014 у Wayback Machine.] by C. Pellicer-Lostao and R. Lopez-Ruiz after work by Ed Pegg Jr, The Wolfram Demonstrations Project.
• Matlab code for the Hénon Map [Архівовано 28 березня 2014 у Wayback Machine.] by M.Suzen
• Simulation [Архівовано 1 лютого 2014 у Wayback Machine.] of Hénon map in javascript (experiences.math.cnrs.fr) by Marc Monticelli.