Кодобуток

Кодобуток (категорна сума) сімейства об'єктів — узагальнення у теорії категорій для понять диз'юнктного об'єднання множин і топологічних просторів та прямої суми модулів або векторних просторів. Кодобуток сімейства об'єктів — це найбільш загальний об'єкт, у який існує морфізм з кожного об'єкта сімейства. Кодобуток об'єктів двоїстий їхньому добутку, тобто визначення кодобутків можна отримати з визначення добутку згортанням усіх стрілок. Проте, насправді добуток і кодобуток об'єктів разюче відрізняються.

Визначення

Нехай ${\mathcal {C}}$ — категорія, $\{X_{j}|j\in J\}$ — індексоване сімейство її об'єктів. Кодобуток цього сімейства — це такий об'єкт $X$, разом з морфізмами $i_{j}\colon \,X_{i}\to X$, які називаються канонічними вкладеннями або канонічними ін'єкціями (хоча вони не зобов'язані бути ін'єкціями), що для будь-якого $Y\in Ob\,{\mathcal {C}}$ та сімейства морфізмів $f_{j}\colon \,X_{j}\to Y$ існує єдиний морфізм $f\colon \,X\to Y$, такий що $f_{j}=f\circ i_{j}$, тобто наступна діаграма комутативна для всіх $j$:

Кодобуток сімейства $\{X_{j}\}$ зазвичай позначають

$X=\coprod _{j\in J}X_{j}$

або

$X=\bigoplus _{j\in J}X_{j}.$

Іноді морфізм $f$ позначають

$f=\coprod _{j\in J}f_{j}:\coprod _{j\in J}X_{j}\to Y$

щоб підкреслити його залежність від $f_{j}$.

Кодобуток двох об'єктів зазвичай позначають $X_{1}\coprod X_{2}$ або $X_{1}\oplus X_{2}$, тоді діаграма набуває вигляду

Відповідно, $f$ позначають при цьому $f_{1}\coprod f_{2}$, $f_{1}\oplus f_{2}$ або $[f_{1},f_{2}]$.

Єдиність результату операції $[-,-]$ можна альтернативно виразити як рівність $[h\circ i_{1},h\circ i_{2}]=h$, справедливу для будь-яких $h$.

Існує еквівалентне визначення кодобутку. Кодобуток сімейства $\{X_{j}|j\in J\}$ — це такий об'єкт $X$, що для будь-якого об'єкта $Y\in C$ функція $Hom(X,Y)\rightarrow \prod _{j\in J}Hom(X_{j},Y)$, задана як $u\mapsto \{u\circ i_{j}\}$, бієктивна.

Властивості

• Якщо сума об'єктів існує, то вона єдина з точністю до ізоморфізму.
• Комутативність: $a+b\simeq b+a.$
• Асоціативність: $(a+b)+c\simeq a+(b+c)$
• Якщо у категорії існує початковий об'єкт $\ 0$, то $a+0\simeq 0+a\simeq a.$
• Категорія, в якій визначено добуток будь-яких двох об'єктів і є ініціальний об'єкт, є симетричним моноїдом.

Дистрибутивність

У загальному випадку існує канонічний морфізм $X\times Y+X\times Z\to X\times (Y+Z)$, де плюс позначає кодобуток об'єктів. Це випливає із існування канонічних проєкцій і вкладень та з комутативності наступної діаграми:

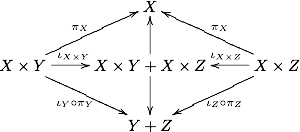
Властивість універсальності для $X\times (Y+Z)$ гарантує при цьому існування шуканого морфізму. Категорія називається дистрибутивною, якщо у ній цей морфізм є ізоморфізмом.

Матриця перетворень

Будь-який морфізм

$f\colon \bigoplus _{i\in I}a_{i}\to \bigotimes _{j\in J}b_{j}$

породжує множину морфізмів

$f_{ij}\colon a_{i}\to b_{j}$,

які задаються за правилом $f_{ij}=\pi _{j}\circ f\circ \imath _{i}$ і називаються матрицею перетворення. В інший бік, будь-яка матриця перетворення $f_{ij}\colon a_{i}\to b_{j}$ задає єдиний відповідний морфізм $\scriptstyle f\colon \bigoplus _{i\in I}a_{i}\to \bigotimes _{j\in J}b_{j}.$ Якщо у категорії існує нульовий об'єкт $0,$ для котрого для будь-якого об'єкта $x$ існує єдиний морфізм $d_{x}\colon x\to 0$ і єдиний морфізм $c_{x}\colon 0\to x$, то матриця перетворення $f_{ij}\colon a_{i}\to a_{j}$, яка визначається за правилом

$f_{ij}=\left\{{\begin{matrix}c_{j}\circ d_{i},~i\neq j\\id_{i},~i=j\end{matrix}}\right.$

називається одиничною матрицею.

Приклад

В категорії скінченновимірних векторних просторів ${\mathcal {V}}ect_{f}$ кодобуток просторів збігається з їхнім добутком і є їхньою прямою сумою. У цьому випадку категорне та звичайне поняття матриці перетворень збігаються, так як будь-який скінченновимірний простір можна розкласти у пряму суму одновимірних. При цьому матриця перетворення усього простору задається шляхом наведення образів відповідних базисних векторів та продовження перетворення на весь простір за лінійністю єдиним чином.

Література

• С. Мак Лейн Категории для работающего математика. — [[{{{1}}} (станція метро)|{{{1}}}]]: Физматлит, 2004 [1998].

Див. також

• Добуток (теорія категорій) — двоїсте поняття.