Рівняння шостого степеня

Графік функції многочлена 6-го степеня, який має 6 дійсних коренів (перетин осі х) та 5 критичних точок. У залежності від кількості і вертикального розташування мінімумів і максимумів, многочлен може мати 6, 4, 2, або не мати дійсних коренів. Число комплексних коренів буде відповідно 6 мінус кількість дійсних коренів.

У математиці рівняння шостого степеня має такий загальний вигляд:

$ax^{6}+bx^{5}+cx^{4}+dx^{3}+ex^{2}+fx+g=0,\,$

де a ≠ 0 , а коефіцієнти a, b, c, d, e, f, g , можуть бути цілими, раціональними, дійсними, комплексними числами або в більш загальному випадку — елементами будь-якого алгебраїчного поля.

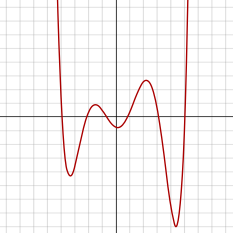
Функція шостого степеня — функція, визначена многочленом 6-го степеня. Оскільки вона парного степеня, то графічно подібна на функцію 4-го степеня, крім того може мати додатковий локальний максимум і локальний мінімум. Похідна від функція 6-го степеня — функція 5-го степеня.

Оскільки функція 6-го степеня є многочленом парного степеня, вона має нескінчену границю, коли аргумент прямує до додатної або від'ємної нескінченності. Якщо старший коефіцієнт a додатній, то функція зростає до плюс нескінченості по обидві боки і таким чином функція має глобальний мінімум. Аналогічно, якщо a від'ємний, функція 6-го степеня спадає до мінус нескінченності і має глобальний максимум.

Алгоритми розв'язання

Згідно теореми Абеля — Руффіні, рівняння шостого степеня в загальному вигляді не можна розв'язати в радикалах. Еварист Галуа розробив методи для визначення можливості розв'язання конкретних рівнянь у радикалах, що привело до створення теорії Галуа.

Спроби побудувати загальну теорію розв'язання рівняння шостого степеня була здійснена у 1886 році Френком Коулом. За вісім років до цього, Фелікс Кляйн запропонував методи розв'язання рівняння п'ятого степеня і робота Коула намагалася узагальнити ці підходи до рівнянь 6-го степеня.

У подальших роботах математиків було встановлено, що рівняння 6-го степеня можна розв'язати в радикалах, якщо його група Галуа порядку 48, яка стабілізує розбиття множини коренів на три підмножини з двох коренів або в групі порядку 72, яка стабілізує розбиття множини коренів на дві підмножини з трьох коренів.

В 2000 році Томас Хагедорн (англ. Thomas R. Hagedorn) опублікував формули для тестування будь-якого випадку і, якщо рівняння розв'язується в радикалах, обчислити ці корені.

Загальне рівняння шостого степеня може бути розв'язана у функціях Кампе де Ферьє. Більш обмежений клас рівнянь може бути вирішений гіпергеометричними функціями однієї змінної, використовуючи підходи Фелікса Кляйна до розв'язання рівнянь п'ятого степеня.

Окремі випадки

Триквадратне рівняння

Триквадратне рівняння — алгебраїчне рівняння виду

$ax^{6}+bx^{3}+c=0.$

Заміною $t=x^{3}$ воно зводиться до квадратного рівняння

$at^{2}+bt+c=0.$

Бікубічне рівняння

Бікубічне рівняння — це алгебраїчне рівняння виду

$ax^{6}+bx^{4}+cx^{2}+d=0.$

Заміною $t=x^{2}$ воно зводиться до кубічного рівняння

$at^{3}+bt^{2}+ct+d=0.$

Приклади використання

Крива Ватта, яка виникла в результаті робіт Джеймса Ватта зі створення парового двигуна — рівняння 6-го степеня з двома змінними.

Див. також

• Кубічне рівняння.