Граф Паппа

Граф Паппа

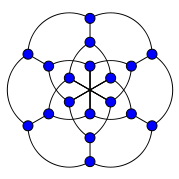
В Теорії графів графом Паппа називається двочастковий кубічний (або 3-регулярний) неорієнтований граф з 18 вершинами і 27 ребрами, є графом Леві конфігурації Паппа. Він названий на честь Паппа Олександрійського, математика Стародавньої Греції, який вірив, що довів теорему про шестикутник, в якій описував конфігурацію Паппа. Всі кубічні дистанційно-регулярні графи відомі. Граф Паппа — один з тринадцяти таких графів.

Число прямолінійних схрещень графу Паппа дорівнює 5, і цей граф є найменшим кубічним графом з таким числом схрещень (послідовність A110507 з Онлайн енциклопедії послідовностей цілих чисел, OEIS). Граф має обхват 6, діаметр 4, радіус 4, хроматичне число 2, хроматичний індекс 3, а також є і 3-вершинно-зв'язним, і 3-реберно-зв'язним.

Хроматичний поліном графу Паппа дорівнює $(x-1)x(x^{16}-26x^{15}+325x^{14}-2600x^{13}+14950x^{12}-65762x^{11}+$$229852x^{10}-653966x^{9}+1537363x^{8}-3008720x^{7}+4904386x^{6}-$$6609926x^{5}+7238770x^{4}-6236975x^{3}+3989074x^{2}-1690406x+356509)$.

Назва «Граф Паппа» використовується також для близького графу з дев'ятьма вершинами, на вершині для кожної точки конфігурації Паппа з ребрами для кожної пари точок, що перебувають на одній лінії. Цей граф 6-регулярний і є доповненням об'єднання трьох не пов'язаних один з одним трикутних графів. Перший граф Паппа можна вкласти в тор, отримуючи при цьому правильну карту з дев'ятьма шестикутними гранями. Другий граф утворює при такому вкладенні правильну карту з 18 трикутними гранями.

Алгебраїчні властивості

Група автоморфізмів графу Паппа — це група з порядком 216. Вона діє транзитивно на вершини і ребра графу. Таким чином, граф Паппа є симетричним. У нього є автоморфізми, що переводять будь-яку вершину в будь-яку іншу і будь-яке ребро — у будь-яке інше ребро. У списку Фостера граф Паппа позначено як F018A і він є єдиним кубічним симетричним графом з 18 вершинами. Характеристичний поліном графу Паппа дорівнює $(x-3)x^{4}(x+3)(x^{2}-3)^{6}$ . Це єдиний граф з таким характеристичним поліномом, так що в даному випадку граф визначається своїм спектром.

Галерея

• 
  Граф Паппа, розфарбований для виділення різних циклів.
• 
  Хроматичний індекс графу Паппа дорівнює 3.
• 
  Хроматичне число графу Паппа дорівнює 2.