Цефеїда

Цефеї́да (від назви зорі δ Цефея) — назва класу пульсуючих змінних зір (гігантів та надгігантів) спектральних класів F5-F8 (у максимумі блиску) з амплітудами від кількох сотих до 2,0m та періодами коливання від 1 до 135 діб.
Причиною змінності цефеїд є пульсація зовнішніх шарів зорі. Це призводить до періодичної зміни температури та радіусу. Найбільша світність приблизно відповідає моменту найшвидшого розширення зорі[1]. Зміна розміру цефеїд може сягати кількох радіусів Сонця.
10 вересня 1784 року Едвард Піготт виявив змінність η Орла[en], першого відомого представника класу класичних змінних цефеїд. Змінність Дельта Цефея виявив Джон Ґудрайк кількома місяцями пізніше і від неї походить назва типу. До кінця 19 століття кількість подібних змінних зросла до кількох десятків, і їх виділили в окремий тип[2]. Більшість цефеїд були відомі завдяки характерним формам кривих блиску зі швидким зростанням яскравості та горбом, але деякі з більш симетричними кривими блиску були відомі як Близнюки на честь прототипу ζ Близнят[3][відсутнє в джерелі].
1908 року Генрієтта Свон Лівітт виявила 1777 змінних зір у Малій Магеллановій Хмарі. Для 16 з них вона визначила періоди змінності; виявилося, що яскравіші зорі мають довший період. Враховуючи велику відстань до Магелланової хмари (порівняно з розмірами самого об'єкта), ці досліди було інтерпретовано як залежність світності (а не лише видимої зоряної величини) від періоду. Тоді ще не було достеменно відомо, що відкриті зорі є цефеїдами. На це вперше звернув увагу Ейнар Герцшпрунг 1913 року. Він же висунув ідею про використання цієї залежності для визначення космічних відстаней. Він визначив паралакси тринадцяти цефеїд, обчислив відстані до них і, таким чином, побудував першу шкалу міжзоряних відстаней[4][5][6]. Пізніше його результати були переглянуті, а розрахунки уточнені[7].
На початку 20 століття не існувало єдиного консенсусу щодо форми і розмірів Всесвіту, а також того, чи є наша Галактика єдиним великомасштабним об'єктом у Всесвіті (так звана теорія «острівного Всесвіту», англ. «island universe» theory) чи існують інші подібні їй. Кульмінацією цих суперечок був Великий диспут, який відбувся в 1920 році. Йому передувала значна кількість досліджень, мета яких полягала у вимірюванні форми та розмірів Чумацького Шляху. У 1918 році Гарлоу Шеплі, який був прихильником теорії «острівного Всесвіту», застосував цефеїди, щоб оцінити розмір і форму Чумацького Шляху та розміщення Сонця в ньому[8]. У 1924 році Едвін Габбл виявив цефеїди в галактиці Андромеди, до того часу відомій як «Туманність Андромеди», визначив відстань до них і показав, що ці зорі не є об'єктами Чумацького Шляху. Відкриття Габбла вирішило питання, яке ставилося у «Великій дискусії» про те, чи являє собою Чумацький Шлях весь Всесвіт, чи це лише одна з багатьох галактик у Всесвіті[9].

1929 року Габбл зіставив швидкість віддалення 23 галактик (за спектральними вимірами Весто Слайфера) із відстанями до них, які він визначив за цефеїдами. Його результати надійно підтвердили розширення Всесвіту, яке за два роки до того передбачив Жорж Леметр із простіших міркувань[11][12].
У середині 20-го століття стали помітні проблеми з астрономічною шкалою відстаней, які привели до висновку, що цефеїди є неоднорідною групою об'єктів із досить різними властивостями. У 1940-х роках Вальтер Бааде розділив популяцію цефеїд на дві: класичні цефеїди та цефеїди типу II[13][14]. Фундаментальне відкриття Бааде збільшило відстань до M31 удвічі та призвело до перегляду шкали міжгалактичних відстаней. Змінні типу RR Ліри, які тоді називали «корокоперіодичними цефеїдами» або «змінними скупчень»[15], також досить швидко виділили в окремий клас змінності.
Механізм пульсації цефеїд в узагальненому вигляді (як теплової машини) запропонував 1926 року Артур Стенлі Еддінгтон (який багато писав про динаміку цефеїд)[16], але лише в 1953 році Сергій Жевакін[en] запропонував конкретний механізм пульсацій, який зараз називають каппа-механізмом[17].
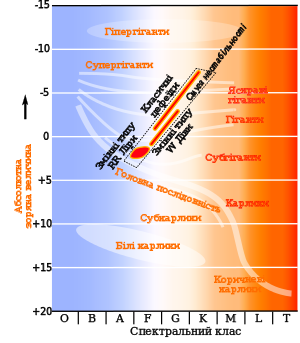
Цефеїди є гігантами і надгігантами спектральних класів F, G і раннього K. Їхній блиск змінюється з амплітудою від кількох сотих до 2m (у смузі V) із періодом від 1 до 135 діб[18][19], а спектральний клас — від F5—F8 у максимумі до F7—K1 у мінімумі. Максимуми блиску, температури і швидкості розширення цефеїд майже збігаються, проте не припадають ні на максимум, ні на мінімум радіуса. Криві блиску цефеїд вирізняються доволі швидким зростанням яскравості та повільнішим спадом[20][21][22].
Характерні періоди пульсацій добре вивчених цефеїд становлять від 1 до 45 діб, однак трапляються цефеїди і з довшими періодами пульсацій. У нашій Галактиці трапляються цефеїди з періодом 125 діб, а в інших галактиках (зокрема, в Магелланових Хмарах) відомі об'єкти з періодами більше 200 діб, що мають усі ознаки цефеїд[20][22].
Криві блиску змінних зір типу RR Ліри мають деяку схожість із кривими блиску цефеїд, і з цієї причини в минулому для зір типу RR Ліри застосовувався термін «короткоперіодичні цефеїди». Однак між цефеїдами і зорями типу RR Ліри є і більш фундаментальні фізичні відмінності, крім періодів, тому такий термін вважається некоректним і більше не використовується[22].
Більшість цефеїд можна віднести до одного з двох типів: до класичних цефеїд, що належать до плоскої підсистеми Галактики та зоряного населення I, або до віргінід, що надежать до сферичної підсистеми Галактики та населення II. Цей поділ цефеїд на два класи запровадив Вальтер Бааде в 1952 році. Він виявив, що не всі цефеїди підпорядковуються єдиній залежності період — світність і з'ясував, що деякі відстані, визначені на той час цим методом, виявилися хибними: приміром, оцінка відстані до Галактики Андромеди була занижена вдвічі[23][20][24].
Це старі зорі населення I, які концентруються в плоскій підсистемі Галактики та, як правило, трапляються в розсіяних зоряних скупченнях. Ці цефеїди мають масу 3-18 M☉, абсолютні зоряні величини від −0,5m до −6m і періоди, що найчастіше лежать в інтервалі 5-10 діб, а їхній вік становить 50-300 мільйонів років. На початкових стадіях еволюції, коли ці зорі перебували на головній послідовності, вони мали спектральний клас B. Цей тип цефеїд добре вивчений і має досить точно визначену залежність період — світність, і, як правило, застосовується для визначення відстані[25][26][27][20]. Прикладами класичних цефеїд є η Орла[en] та δ Цефея — перші з відкритих цефеїд узагалі, а також Полярна зоря — вона є найближчою до Землі цефеїдою, хоча 2011 року її блиск змінювався з амплітудою лише 0,06m[28][29].
Криві блиску класичних цефеїд характеризуються швидким підйомом та повільнішим спадом. Для періодів, менших 6 діб вони гладенькі. У зір із періодом близько 6 діб на спаді кривої з'являється опуклість. Зі збільшенням періоду опуклість перетворюється на горб та наближається до максимуму; у цефеїд із періодами близько 9—10 діб горб розташований поблизу максимуму блиску, що може призвести до наявності двох максимумів. У цефеїд із періодом понад 10 діб горб «переповзає» через максимум і спостерігається вже на підйомі кривої блиску[22]. Пояснюють це явище або пульсацією у двох періодах із резонансом 1:2, або відлунням від самих пульсацій. В англійській літературі такі цефеїди називають bump cepheids (дослівно — «горбаті цефеїди»)[29][30].
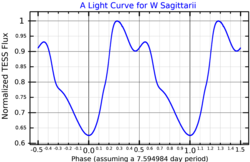
- Приклади кривих блиску цефеїд (за даними супутника TESS)
-
Період 6,22 діб. Опуклість на спаді блиску майже непомітна.
-
Період 6,8 діб. На спаді помітна опуклість.
-
Період 7,5 діб. На спаді кривої виражений горб.
-
Період 7,6 діб. Горб більшає та наближається до максимуму.
Віргініди[31] — старі зорі популяції II, що належать до кулястої підсистеми Галактики і мають низьку металічність. Вони трапляються здебільшого в кулястих скупченнях і підпорядковуються іншій залежності період — світність, аніж класичні цефеїди: за однакових періодів віргініди тьмяніші на 1,5m — тобто, приблизно вчетверо[20]. Абсолютні зоряні величини таких зір лежать у діапазоні від 0m до -3m, а період лежить у межах від 2 до 45 діб (зазвичай 12-28 діб)[32]. Їх вік становить понад 10 мільярдів років[33][20][22].
Віргініди поділяють на 2 підкласи[34][29]:
- змінні типу BL Геркулеса — із періодами від 1 до 8 діб;
- змінні типу W Діви — із періодами понад 8 діб.
Деякі дослідники разом із віргінідами розглядають також змінні RV Тельця, хоча вони перебувають на іншій стадії зоряної еволюції[26], і об'єднують їх у цефеїди типу II[27]. Маси цефеїд типу II вимірювалися тільки побічно, за їхніми пульсаціями, і вважалося, що вони лежать у діапазоні 0,5-0,8 M☉[35].
Крім двох основних типів, відомі так звані «аномальні цефеїди»: вони трапляються в карликових сфероїдальних галактиках і мають світності та періоди, які відповідають проміжним значенням між цефеїдами I типу та II типу. Прототипом для цього класу стала зоря BL Волопаса, і, відповідно, такі зорі стали називати змінними типу BL Волопаса. Передбачається, що такі об'єкти мають маси близько 1,5 M☉. Термін «аномальні цефеїди» застосовувався для опису цефеїд типу W Діви невдовзі після їх відкриття, але зараз у такому значенні не вживається[27][22].
Бі- і мультимодальні цефеїди — зорі, що пульсують у двох або більше різних періодах. Якщо періоди близькі, то в пульсаціях цефеїд виникають биття. Близько половини цефеїд із періодами від 2 до 4 діб є бімодальними[29][36][37][38].

Однією з найважливіших особливостей цефеїд, що зумовила надзвичайно велике значення цих зір в астрономії, є встановлена залежність між періодом пульсацій та світністю зорі[22]. Ця залежність декілька разів переглядалася та уточнювалася. Для класичних цефеїд за сучасними даними вона має вигляд:
де MV — абсолютна зоряна величина у жовтих (видимих) променях; P — період зміни блиску.
У 1908 році Генрієтта Лівітт відкрила залежність між періодом зміни блиску і світністю цефеїд у Магелланових Хмарах. Зорі там свідомо перебували на одній відстані, а отже, їхні світності можна було порівнювати безпосередньо[39]. У 1913 році Ейнар Герцшпрунг встановив, що цефеїди в Магелланових Хмарах — такі самі, як і на околицях Сонця, і відкрита раніше залежність періоду і світності скрізь однакова. Тоді ж Герцшпрунг ввів саме позначення «цефеїда» — за назвою зорі δ Цефея[40][24]. Відтоді параметри залежності неодноразово уточнювалися. У 1997 році емпірично, на підставі даних Гіппарокс було отримано таку формулу для класичних цефеїд:
Де — середня абсолютна зоряна величина в спектральному діапазоні V, а — період пульсацій у добах[41]. Крім того, 1996 року було отримано узагальнені залежності для різних спектральних діапазонів, що мають схожий вигляд:
Де — деякі числові параметри, які для різних спектральних діапазонів набувають значень, наведених у таблиці[22][20].
| Спектральний
діапазон |
||
|---|---|---|
| B | −2,40 | −0,73 |
| V | −2,87 | −1,01 |
| RC | −2,97 | −1,30 |
| R | −3,13 | −1,32 |
| IC | −3,07 | −1,46 |
| I | −3,18 | −1,60 |
| J | −3,37 | −1,69 |
| H | −3,52 | −1,85 |
| K | −3,52 | −1,94 |
Тим часом, навіть за досить точних даних зоряні величини і періоди не ідеально вкладаються у вищевказану залежність. На неї впливає також положення цефеїди на смузі нестабільності, яке може бути виражене показником кольору. У 2007 році було запропоновано таку формулу, що використовує показник кольору [42]:
Зв'язок періоду і світності пояснюється тим, що і період, і світність цефеїди збільшуються зі збільшенням маси. Крім того, що більша маса зорі, то менший загальний термін її життя і її вік у момент, коли вона стає цефеїдою. Таким чином, усі чотири параметри виявляються пов'язаними[43].
Зазвичай зорі перебувають у термодинамічній рівновазі, тобто внутрішній тиск газу в зорі та її власна вага врівноважені. Якщо вона порушується, зокрема, зоря розширюється або стискається, вона прагне повернутися до стану рівноваги і в ній починаються коливання. Період таких коливань — власний період , пов'язаний із середньою густиною зорі наступним чином[20]:
Де — гравітаційна стала. Наприклад, для Сонця, що має середню густину 1,4 г/см3, період становитиме трохи менше години. Можливість таких пульсацій передбачив 1879 року німецький фізик Август Ріттер, а 1894 року Аристарх Бєлопольський виявив зміни променевої швидкості цефеїд. Спочатку припускали, що ці зміни спричинені наявністю невидимих масивних супутників, але потім з'ясувалося, що вони пояснюються радіальними пульсаціями[20][44].
У 1918—1926 роках Артур Еддінгтон опублікував цикл робіт, присвячених адіабатичним радіальним власним коливанням газових куль (якими є зорі). Едінгтон довів, що такі власні коливання мають швидко згасати й для підтримання зоряних пульсацій необхідний механізм перетворення теплової (чи променевої) енергії на механічну енергію пульсацій. Він також запропонував два можливих варіанти такого механізму. Другий із них полягав у тому, що непрозорість зоряної речовини може збільшуватися від стиснення[45]. Цей механізм іноді називають клапанним, тому що деякий фізичний процес регулює надходження тепла подібно до клапана. Едінгтон не ідентифікував фізичну природу такого механізму[22].
Це вдалося зробити радянському вченому Сергію Олександровичу Жевакіну[en] у 1949—1956 роках[17][46][47]. Він побудував модель пульсацій, у якій «клапаном» виступали зони подвійної критичної іонізації гелію. Це зони, у яких гелій спочатку іонізується до «голого» ядра (із поглинанням енергії), а потім рекомбінує до іону He+ (із випромінюванням енергії). Таким чином, енергія затримується в зоні на деякий час, тобто, надходження енергії до поверхні частково перекривається[48][20].
Сам механізм полягає в такому: у цефеїдах є шар іонізованого гелію товщиною в 1-2 % радіуса зорі. Двічі іонізований гелій (He III) менш прозорий, ніж одноразово іонізований гелій (He II). Зі зростанням температури все більша частина гелію стає двічі іонізованою. Через це шар гелію стає менш прозорим, він починає затримувати енергію. Після майже повної (критичної) іонізації гелію температура в шарі починає зростати, через що зоря розширюється. Під час розширення температура шару падає, відбувається часткова рекомбінація He III й перетворення його на He II з випромінюванням енергії, а сам шар стає прозорішим, пропускаючи променисту енергію в зовнішні шари. Зі зменшенням температури тиск у шарі падає, під дією сили тяжіння він знову стискається, і процес повторюється. Інша розповсюджена цього механізму — каппа-механізм, оскільки непрозорість зоряної речовини (англ. opacity) астрономи позначають грецькою літерою «κ» (каппа). У зорях із різними масами розподіл температури в надрах відрізняється, і що масивніша зоря, то ближче до поверхні розташована зона з потрібною температурою, яка становить 35000-55000 K[44][20]. За сучасними даними значну роль у пульсаціях відіграють також зони іонізації водню. Вони розташовані безпосередньо під фотосферою зорі[1].
Коливання можуть підтримуватися тільки в тому разі, якщо їхній період збігається з власним періодом коливань зорі. При збільшенні маси зменшується густина зорі і збільшується період коливань і світність, чим і викликана спостережувана залежність період — світність[43].
Каппа-механізм може підтримувати пульсації не лише цефеїд, але параметри зір, які можуть пульсувати, обмежені. На діаграмі Герцшпрунга-Рассела вони утворюють смугу нестабільності[20][43].
Каппа-механізм є основною причиною пульсацій, але є ще дві другорядні. Суть першої з них полягає в тому, що шар іонізованого гелію має нижчу температуру, ніж сусідні шари, через що частина енергії переходить до нього, посилюючи каппа-механізм, — це явище має назву гамма-механізму. Другий носить назву r-механізму або радіус-механізму і полягає в тому, що під час стиснення зорі зменшується її площа, з якої випромінюється енергія. Щільність енергії всередині зорі зростає, що призводить до розширення оболонок[49][44].
У 1879 році Август Ріттер (1826—1908) продемонстрував, що період адіабатичної радіальної пульсації однорідної сфери пов'язаний з її поверхневою силою тяжіння та радіусом через співвідношення:
де k — константа пропорційності. Тепер, оскільки поверхнева гравітація пов'язана з масою та радіусом сфери через співвідношення:
нарешті отримуємо:
де Q — константа, яка називається постійною пульсації[50].

Під час еволюції зорі змінюють свої параметри, так само як і положення на діаграмі Герцшпрунга-Рассела. Коли в надрах зір внаслідок синтезу закінчується водень, вони починають збільшуватися в розмірах і охолоджуватися, сходячи з головної послідовності та переходячи на стадію субгігантів. У цей час масивні зорі можуть перейти смугу нестабільності та на деякий час стати цефеїдами — на цій стадії такий перехід займає 102−104 років, що дуже мало за астрономічними мірками. Після цього зоря переходить на гілку червоних гігантів, і, якщо її маса досить велика, то гелій у ній вступає в термоядерну реакцію поступово, через що зоря переходить на так звану блакитну петлю. Залежно від маси, зоря на блакитній петлі може перетнути смугу нестабільності до двох разів і перебувати на ній значно довше, ніж під час першого проходження. У деяких випадках зоря може двічі пройти блакитну петлю, і, відповідно, переходів смуги нестабільності на цій стадії буде чотири[21][51][43].
Цефеїди II типу — маломасивні зорі, які еволюціонують іншим чином. Серед них виділяється три підкласи, які відповідають різним стадіям еволюції зір. Після того, як у ядрі маломасивної зорі спалахує гелій, вона переходить на горизонтальну гілку — світності зір на ній практично однакові, а температури залежать від маси та металічності. Горизонтальна гілка перетинається зі смугою нестабільності, і зорі на перетині цих двох областей пульсують — вони відомі як змінні типу RR Ліри. Однак якщо зоря потрапить на високотемпературну частину горизонтальної гілки, то пульсувати вона в цей час не буде. Коли в її ядрі закінчиться гелій, вона почне розширюватися й охолоджуватися, потрапить на асимптотичну гілку гігантів, у деякий момент опиниться на смузі нестабільності та почне пульсувати — у такому разі зоря стане змінною типу BL Геркулеса[27][35].
Якщо ж зоря потрапляє на низькотемпературну частину горизонтальної гілки, то асимптотична гілка гігантів не перетинається зі смугою нестабільності. Однак у зорях наприкінці асимптотичної гілки гігантів може відбуватися зміна шарового водневого джерела на гелієве і назад, через що температура зорі може ненадовго підвищуватися, а сама зоря — проходити блакитну петлю. Якщо зоря при цьому переходить смугу нестабільності і починає пульсувати, то вона стає змінною типу W Діви[27][35][52][53].
Після закінчення асимптотичної гілки гігантів маломасивні зорі скидають оболонку і стають білими карликами, але перед цим температура їхньої поверхні збільшується, що також призводить до проходу зорі смуги нестабільності. Зорі, що проходять смугу на цій стадії, стають змінними типу RV Тельця[27][35].
Період зорі пов'язаний не тільки зі світністю, а й із положенням її на смузі нестабільності: за однакових світностей холодніша зоря матиме більший період пульсацій, ніж гарячіша. Через те, що перехід смуги нестабільності під час стадії субгігантів за астрономічними мірками йде дуже швидко, багаторічні систематичні спостереження дозволяють зареєструвати зміни періодів цефеїд. Збільшення періоду означає, що температура фотосфери зменшується і зоря на діаграмі рухається вправо, а зменшення періоду — збільшення температури фотосфери і рух вліво[43].
У Чумацькому Шляху найбільш поширені класичні цефеїди з періодом пульсацій близько 5 діб. При цьому у Великій і Малій Магелланових Хмарах пікові періоди становлять, відповідно, 3,2 і 1,6 доби. Така відмінність пов'язана з тим, що металічності цих супутників менші, ніж у Чумацького Шляху, відповідно, у 2,2 і в 4,8 разів[25].
Від маси зорі та від вмісту важких елементів залежить максимальна температура, яка буде досягнута на блакитній петлі — чим більша маса і чим менша металічність, тим більшою буде максимальна температура, а від неї залежить, чи потрапить зоря на блакитній петлі на смугу нестабільності. Що менша металічність галактики, то менша мінімальна маса зір, які зможуть стати цефеїдами. Оскільки період цефеїди залежить від її маси, то мінімальний період також залежить від металічності. Водночас, найбільше поширені маломасивні зорі, тому цефеїди з мінімальним періодом будуть найбільш численні[25].
Через відомий і повторюваний зв'язок між періодом і світністю цефеїди використовуються як стандартні свічки в астрономії. З їхньою допомогою можна визначати відстані в діапазоні від 100 пк до 20 Мпк, для більшої частини якого вимірювання відстаней методом паралаксів дають дуже низьку точність. Таким чином, цефеїди важливі для визначення відстаней до далеких об'єктів і встановлення шкали відстаней в астрономії[43].
У 1916—1918 роках, на підставі робіт Генрієтти Лівітт і Ейнара Герцшпрунга, Харлоу Шеплі вперше використовував цефеїди як стандартні свічки. Уточнивши співвідношення світності та періоду, він оцінив відстані до найближчих кулястих скупчень; потім, послідовно використовуючи інші критерії, він визначив відстані (близько сотень тисяч світлових років) до віддаленіших скупчень, з'ясував розміри Чумацького Шляху і визначив, що Сонце перебуває на краю Галактики. У 1925—1926 роках Едвін Габбл виявив кілька цефеїд у галактиці Андромеди та обчислив відстань до них, тим самим уперше довівши існування об'єктів поза нашою Галактикою. Надалі за результатами спостережень руху цефеїд було визначено форму спіральних рукавів Чумацького Шляху та швидкість обертання об'єктів у ньому. При цьому більшість цефеїд мають дуже високу світність, тому легко доступні для спостереження ті, що розташовані в сусідніх галактиках, і завдяки цьому цефеїди використовують для визначення відстані до інших галактик, що дає змогу визначити сталу Габбла, і до ще більш яскравих об'єктів — наднових. Прискорене розширення Всесвіту також було відкрито завдяки цефеїдам: виявилося, що фотометрично визначені відстані до найдальших галактик не відповідають швидкості їхнього віддалення[24][43].
Дані про цефеїди та їхня точність дуже важливі: наприклад, помилка у визначенні абсолютної світності цефеїд на 1m призводить до помилки у визначенні відстаней у 1,58 разів, і така сама помилка буде в значенні сталої Габбла, яка визначається за відстанню до цефеїд. Точне визначення залежності період — світність ускладнюється тим, що на цю залежність впливають, наприклад, металічність зорі та її поточне становище на смузі нестабільності, і, зокрема, з цієї причини оцінки сталої Габбла варіюються від 60 до 80 км·с−1·Мпк−1[54].
- ↑ а б Ю. А. Фадеев Пульсации звезд Природа август 2006 г. (рос.)
- ↑ Clarke, Agnes Mary (1903). Problems in Astrophysics. London, England: Adam & Charles Black. с. 319. ISBN 978-0-403-01478-1.
- ↑ Engle, Scott (2015). The Secret Lives of Cepheids: A Multi-Wavelength Study of the Atmospheres and Real-Time Evolution of Classical Cepheids (Дипломна робота). arXiv:1504.02713. Bibcode:2015PhDT........45E. doi:10.5281/zenodo.45252.
- ↑ Shapley, Harlow (December 1914). On the Nature and Cause of Cepheid Variation. Astrophysical Journal. 40: 448. Bibcode:1914ApJ....40..448S. doi:10.1086/142137.
- ↑ Shapley, H. (1916), The variations in spectral type of twenty Cepheid variables, Astrophysical Journal, 44: 273, Bibcode:1916ApJ....44..273S, doi:10.1086/142295.
- ↑ Leavitt, Henrietta S.; Pickering, Edward C. (1912). Periods of 25 variable stars in the Small Magellanic Cloud. Harvard College Observatory Circular. 173: 1—3. Bibcode:1912HarCi.173....1L.
- ↑ Hertzsprung, E. (1913). Über die räumliche Verteilung der Veränderlichen vom δ Cephei-Typus [On the spatial distribution of variable [stars] of the δ Cephei type]. Astronomische Nachrichten (нім.). 196 (4692): 201—208. Bibcode:1913AN....196..201H.
- ↑ Shapley, H. (1918). Globular Clusters and the Structure of the Galactic System. Publications of the Astronomical Society of the Pacific. 30 (173): 42. Bibcode:1918PASP...30...42S. doi:10.1086/122686.
- ↑ Hubble, E. P. (1925). Cepheids in spiral nebulae. The Observatory. 48: 139. Bibcode:1925Obs....48..139H.
- ↑ VISTA Discovers New Component of Milky Way. Процитовано 29 October 2015.
- ↑ Ірина мартин (26 лютого 2019). Всесвіт: безмежний і скінченний. Збруч (інтерв'ю з Богданом Новосядлим). Архів оригіналу за 26 лютого 2019. Процитовано 26 лютого 2019.
- ↑ Lemaître, G. (1927). Un Univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques. Annales de la Société Scientifique de Bruxelles. 47: 49. Bibcode:1927ASSB...47...49L.
- ↑ Baade, W. (1958). Problems in the determination of the distance of galaxies. The Astronomical Journal. 63: 207. Bibcode:1958AJ.....63..207B. doi:10.1086/107726.
- ↑ Allen, Nick. Section 2: The Great Debate and the Great Mistake: Shapley, Hubble, Baade. The Cepheid Distance Scale: A History. Архів оригіналу за Dec 10, 2007.
- ↑ Зорі типу RR Ліри // Астрономічний енциклопедичний словник / за заг. ред. І. А. Климишина та А. О. Корсунь. — Львів : Голов. астроном. обсерваторія НАН України : Львів. нац. ун-т ім. Івана Франка, 2003. — С. 180—181. — ISBN 966-613-263-X.
- ↑ Eddington, A.S. and Eddington, A.S. (1926). Chapter VIII. Variable Stars. The Internal Constitution of the Stars. Cambridge Science Classics. Cambridge University Press. ISBN 9780521337083. LCCN lc87005205. Архів оригіналу за 28 вересня 2015. Процитовано 19 жовтня 2015.
- ↑ а б Жевакин С.А. (1953). К теории цефеид. Астрономический журнал. 30: 161—179.(рос.)
- ↑ N.N. Samus , O.V. Durlevich (12-Feb-2009), GCVS Variability Types, ЗКЗЗ, Moscow: Sternberg Astron. Inst.
- ↑ Variable Star Type Designations. The International Variable Star Index. AAVSO. Version 1.1 [C]. Процитовано 4 січня 2024.
{{cite web}}: Пропущений або порожній|url=(довідка); Проігноровано|chapter=(довідка) - ↑ а б в г д е ж и к л м н Кононович Э.В., Мороз В.И. Общий курс астрономии. ISBN 5-354-00866-2.
- ↑ а б Hannu Karttunen, Pekka Kröger, Heikki Oja, Markku Poutanen, Karl Johan Donner. Fundamental Astronomy. ISBN 978-3-540-00179-9.
- ↑ а б в г д е ж и к Н. Н. Самусь. 2.2 Классические цефеиды. Типы по ОКПЗ: DCEP, DCEPS, CEP(B) // Переменные звёзды. — Учебное пособие по курсу «Астрономия». (рос.)
- ↑ И.Стюарт. Математика космоса: Как современная наука расшифровывает Вселенную. с. 332—542. ISBN 9785961452280.
- ↑ а б в Ефремов Ю. Н. (1986). Цефеиды. Физика космоса: Маленькая энциклопедия.
- ↑ а б в Scott Gerard (2014). The Secret Lives of Cepheids (PDF). Villanova University. Процитовано 15 липня 2020.
- ↑ а б Wallerstein, George. The Cepheids of Population II and Related Stars : [англ.] // The Publications of the Astronomical Society of the Pacific : journal. — 2002. — Vol. 114, № 797. — С. 689—699. — Bibcode: 2002PASP..114..689W. — DOI:10.1086/341698.
- ↑ а б в г д е Soszyński, I.; Udalski, A.; Szymański, M. K.; Kubiak, M.; Pietrzyński, G.; Wyrzykowski, Ł.; Szewczyk, O.; Ulaczyk, K.; Poleski, R. The Optical Gravitational Lensing Experiment. The OGLE-III Catalog of Variable Stars. II.Type II Cepheids and Anomalous Cepheids in the Large Magellanic Cloud : [англ.] // Acta Astronomica : journal. — 2008. — Vol. 58. — С. 293. — arXiv:0811.3636. — Bibcode: 2008AcA....58..293S.
- ↑ Scott Gerard (2014). The Secret Lives of Cepheids (PDF) (Thesis for the degree of Doctor of Philosophy). Villanova University. Процитовано 15 липня 2020.
- ↑ а б в г David Darling. Cepheid variable. Encyclopedia of Science. Процитовано 15 липня 2020.
- ↑ Classical Cepheids. OGLE Atlas of Variable Star Light Curves. Процитовано 7 листопада 2023.
The bump appears on the descending branch of the light curves of Cepheids with periods of about 6 days and for longer periods it progresses backward in phase. Around periods of 10 days, the bump passes through maximum light, then moves down in the ascending branch and disappears for periods longer than 20 days.
- ↑ Цефеїди // Астрономічний енциклопедичний словник / за заг. ред. І. А. Климишина та А. О. Корсунь. — Львів : Голов. астроном. обсерваторія НАН України : Львів. нац. ун-т ім. Івана Франка, 2003. — С. 518. — ISBN 966-613-263-X.
- ↑ Dale E. Gary. Pulsating and Variable Stars. New Jersey's Science & Technology University. Процитовано 15 липня 2020.
- ↑ Our Research: Type II Cepheids as distance indicators with VVV time series. Instituto Milenio de Astrofisika. Процитовано 15 липня 2020.
- ↑ Cepheids (CEP). The International Variable Star Index. AAVSO. 2005-2023 Version 1.1 [C]. Процитовано 26 грудня 2023.
- ↑ а б в г Harris, Hugh C.; Welch, Douglas L. The Binary Type II Cepheids IX CAS and TX Del : [англ.] // Astronomical Journal : journal. — 1989. — Vol. 98 (вересень). — С. 981. — Bibcode: 1989AJ.....98..981H. — DOI:10.1086/115190.
- ↑ Classical Cepheids. OGLE Atlas of Variable Star Light Curves. Процитовано 15 липня 2020.
- ↑ Публикации. Журнал "Переменные звёзды". Астронет. Процитовано 15 липня 2020.
- ↑ Beat Cepheid. Oxford Reference. Процитовано 15 липня 2020.
- ↑ Генриетта Ливитт. 1777 variables in the Magellanic Clouds // Annals of Harvard College Observatory. — 1908. — Т. 60. — С. 87. — Bibcode: 1908AnHar..60...87L.
- ↑ Fernie, J.D. The Period–Luminosity Relation: A Historical Review : [англ.] // Publications of the Astronomical Society of the Pacific : journal. — 1969. — Vol. 81, № 483 (грудень). — С. 707. — Bibcode: 1969PASP...81..707F. — DOI:10.1086/128847.
- ↑ Feast, M. W.; Catchpole, R. M. The Cepheid period-luminosity zero-point from HIPPARCOS trigonometrical parallaxes : [англ.] // Monthly Notices of the Royal Astronomical Society. — 1997. — Vol. 286, № 1. — С. L1—L5.
- ↑ Scott Gerard (2014). The Secret Lives of Cepheids (PDF). Villanova University. Процитовано 15 липня 2020.
- ↑ а б в г д е ж Расторгуев А. С. Цефеиды — звёздные маяки Вселенной. Державний астрономічний інститут імені П. К. Штернберга.
- ↑ а б в Scott Gerard (2014). The Secret Lives of Cepheids (PDF). Villanova University. Процитовано 15 липня 2020.
- ↑ Eddington, A.S. (1926). Chapter VIII. Variable Stars. The Internal Constitution of the Stars. Cambridge Science Classics. Cambridge University Press. ISBN 9780521337083. LCCN lc87005205.(англ.)
- ↑ Жевакин С.А. (1954). К теории звездной переменности. II. Астрономический журнал. 31: 141-153.(рос.)
- ↑ Zhevakin S.A. (1963). Physical Basis of the Pulsation Theory of Variable Stars. Annual Review of Astron. and Astrophys. 1: 367-400. doi:10.1146/annurev.aa.01.090163.002055.(англ.)
- ↑ Smith, D. H. Eddington's Valve and Cepheid Pulsations : [англ.] // Sky and Telescope : magazine. — 1984. — Vol. 68. — С. 519. — Bibcode: 1984S&T....68..519S.
- ↑ M. Heydari-Malayeri. Gamma mechanism. An Etymological Dictionary of Astronomy and Astrophysics. Процитовано 15 липня 2020.
- ↑ Maurizio Salaris; Santi Cassisi (13 December 2005). Evolution of Stars and Stellar Populations. John Wiley & Sons. с. 180. ISBN 978-0-470-09222-4.
- ↑ Scott Gerard (2014). The Secret Lives of Cepheids (PDF). Villanova University. Процитовано 15 липня 2020.
- ↑ Groenewegen, M. A. T.; Jurkovic, M. I. (2017). Luminosities and infrared excess in Type II and anomalous Cepheids in the Large and Small Magellanic Clouds. Astronomy and Astrophysics. 603: A70. arXiv:1705.00886. Bibcode:2017A&A...603A..70G. doi:10.1051/0004-6361/201730687.
- ↑ van Loon, J. Th. On the metallicity dependence of the winds from red supergiants and Asymptotic Giant Branch stars // Stellar Evolution at Low Metallicity: Mass Loss, Explosions, Cosmology ASP Conference Series. — 2006.
- ↑ Cepheid Variable Stars & Distance Determination. Australia Telescope National Facility. Процитовано 15 липня 2020.
| Ця сторінка належить до добрих статей української Вікіпедії. |