Користувач:Masich 0/Многокутник видимості (4)
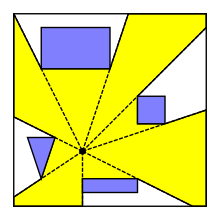
У обчислювальній геометрії видимим полігоном або областю видимості точки р на площині серед перешкод є, можливо, необмежена многокутна область всіх точок площини, видима з p. Полігон видимості також може бути визначений для видимості з сегмента або многокутника. Полігони видимості корисні в робототехніці, відеоіграх і у визначенні позицій для визначення місця розташування об'єктів, таких як найкраще розміщення охоронців в художній галереї.
Якщо видимість многокутника обмежена, то це зіркоподібний многокутник. Полігон видимості обмежений, якщо все промені, які виходять з точки, в кінцевому підсумку закінчуються деякою перешкодою. Це має місце, наприклад, якщо перешкоди - це ребра простого многокутника, а p знаходиться всередині многокутника. В останньому випадку многокутник видимості може бути знайдений за лінійний час. [1][2][3][4]
Формально ми можемо визначити проблему многокутника з плоскою видимістю. Нехай безліч перешкод (відрізків або многокутників) в .Нехай - точка в є безліччю точок в , таких, що для будь-якої точки з , відрізок не перетинає ніяка перешкода в .
Аналогічно, многокутник видимості сегмента або крайової видимий многокутник - це частина, видима будь-якій точці вздовж
Полігони видимості корисні в робототехніці. Наприклад, при локалізації робота робот, який використовує такі датчики, як лідар, виявляє перешкоди, які він може бачити, що аналогічно видимості полігону.[5]
Вони також корисні у відеоіграх, з численними онлайн-підручниками, що пояснюють прості алгоритми його реалізації. [6][7][8]
Численні алгоритми були запропоновані для обчислення полігонів точкової видимості. Для різних варіантів проблеми (наприклад, різних типів перешкод) алгоритми розрізняються по тимчасовій складності.
Наївні алгоритми легко зрозуміти і реалізувати, але вони не оптимальні, так як вони можуть бути набагато повільніші, ніж інші алгоритми.
У реальному житті крапка, що світиться, висвітлює видиму їй область, тому що вона випромінює світло в усіх напрямках. Це можна змоделювати, стріляючи променями з багатьох напрямків. Припустимо, що є точка і множина перешкод Тоді псевдокод може бути виражений наступним чином:
Algorithm naive_bad_algorithm(, ) := for : // shoot a ray with angle := for each obstacle in : := min(, distance from to the obstacle in this direction) add vertex to return
Тепер, якби можна було спробувати всю нескінченну множину кутів, результат був би правильним. На жаль, неможливо дійсно спробувати кожен напрямок через обмеження комп'ютерів. Апроксимація може бути створена шляхом накладення безлічі, скажімо, 50 променів, розташованих рівномірно один від одного. Однак це не точне рішення, так як малі перешкоди можуть бути пропущені двома сусідніми променями цілком. Крім того, він дуже повільний, тому що для отримання приблизно такого ж рішення може знадобитися багато променів, і багатокутник вихідної видимості може мати в собі набагато більше вершин, ніж необхідно.
Описаний раніше алгоритм може бути значно покращено як за швидкістю, так і за правильністю результатів, зробивши спостереження, що досить тільки розстрілювати промені по вершинах кожної перешкоди. Це пов'язано з тим, що будь-які вигини або кути уздовж кордону видимого багатокутника повинні бути обумовлені деяким кутом (тобто вершиною) на перешкоді.
Algorithm naive_better_algorithm(, ) := for each obstacle in : for each vertex of : // shoot a ray from to := distance from to := angle of with respect to for each obstacle in : := min(, distance from to ) add vertex to return
Тимчасова складність цього алгоритму - . Це пов'язано з тим, що алгоритм відстрілює промінь для кожної з вершин, і щоб перевірити, де закінчується промінь, він повинен перевірити перетин з кожною з перешкод. Цього достатньо для багатьох простих додатків, таких як відеоігри, і тому багато навчальних онлайн-посібників вчать цьому методу. Однак, як ми побачимо пізніше, алгоритми швидкіші.

Для простого многокутника і точки , яку видно з. Такий алгоритм був вперше запропонований в 1981 році. Однак він досить складний. У 1983 році був запропонований концептуально більш простий алгоритм, який мав незначну помилку, яка була виправлена в 1987 році.
де , то затемненні вершини з буде складатися з усіх видимих вершин, тобто, це бажаний многокутник видимості. Ефективна реалізація була опублікована в 2014 році.
Для точки в многокутнику з дірами і вершинами в загальному випадку можна показати, що в гіршому випадку алгоритм є оптимальним. Такий алгоритм був запропонований в 1995 році разом з доказом його оптимальності.[9] Проте, він спирається на лінійний алгоритм тріангуляції многокутника по Chazelle, який є надзвичайно складним.

Для точки з набору сегментів, які не перетинаються, за винятком їх кінцевих точок, можна показати, що в гіршому випадку алгоритм є оптимальним. Це пов'язано з тим, що алгоритм многокутника видимості повинен виводити вершини многокутника видимості в відсортованому порядку, тому проблему сортування можна звести до обчислення многокутника видимості.[10]
Зверніть увагу, що будь-який алгоритм, який обчислює видимість многокутника для точки серед сегментів, може бути використаний для обчислення многокутника видимості для всіх інших видів полігональних перешкод, так як будь-який многокутник може бути розкладений на сегменти.
Алгоритмрозділяй і володарюй для обчислення багатокутника видимості був запропонований в 1987 році. [11]
У 1985[12] і 1986 рр. була запропонована кутова розгортка, тобто алгоритм розгортки площини обертання для обчислення видимого многокутника. Ідея полягає в тому, щоб спочатку впорядкувати всі кінцеві точки сегмента під полярним кутом, а потім виконати ітерацію по ним у цьому порядку. Під час ітерації рядок події збурігається як купа. Ефективна реалізація була опублікована в 2014 році.[13]
кількість вершин, де
- VisiLibity: A free open source C++ library of floating-point visibility algorithms and supporting data types, calculates visibility polygons in polygonal environments with polygonal holes
- visibility-polygon-js: A public domain Javascript library for computing a visibility polygon for a point among segments using the angular sweep method
- ↑ Franco P. Preparata and Michael Ian Shamos (1985). Computational Geometry - An Introduction. Springer-Verlag. 1st edition: ISBN 0-387-96131-3; 2nd printing, corrected and expanded, 1988: ISBN 3-540-96131-3; Russian translation, 1989: ISBN 5-03-001041-6.
- ↑
{{cite journal}}: Порожнє посилання на джерело (довідка) - ↑
{{cite journal}}: Порожнє посилання на джерело (довідка) - ↑
{{cite journal}}: Порожнє посилання на джерело (довідка) - ↑
{{cite conference}}: Порожнє посилання на джерело (довідка) - ↑ Liow, Nicklaus. SIGHT & LIGHT how to create 2D visibility/shadow effects for your game. Процитовано 9 May 2014.
- ↑ Patel, Amit (5 July 2012). 2d Visibility Algorithm. Процитовано 9 May 2014.
- ↑ Patel, Amit (5 July 2012). Blobs in Games: 2d Visibility. Процитовано 9 May 2014.
- ↑ Heffernan, Paul; Mitchell, Joseph (1995). An optimal algorithm for computing visibility in the plane. SIAM Journal on Computing. 24 (1): 184—201. doi:10.1137/S0097539791221505.
- ↑ Suri, Subhash; O'Rourke, Joseph (1986). Worst-case optimal algorithms for constructing visibility polygons with holes. Symposium on Computational geometry. ACM. с. 14—23. doi:10.1145/10515.10517.
- ↑ Arkin, E; Mitchell, Joseph (1987). An optimal visibility algorithm for a simple polygon with star-shaped holes (Технічний звіт). № 746. Cornell University Operations Research and Industrial Engineering.
- ↑ Asano, Tetsuo (1985). An efficient algorithm for finding the visibility polygon for a polygonal region with holes. Institute of Electronics, Information, and Communication Engineers. Т. 68, № 9. с. 557—559.
- ↑ Bungiu, Francisc; Hemmer, Michael; Hershberger, John; Huang, Kan; Kröller, Alexander (2014). Efficient Computation of Visibility Polygons. arXiv:1403.3905 [cs.CG].
[[Категорія:Геометричні алгоритми]] [[Категорія:Многокутники]]
















