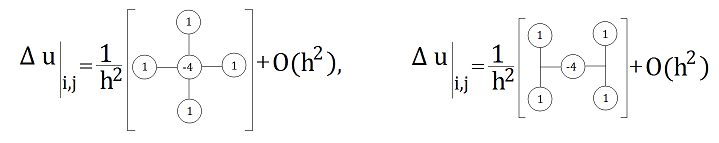Крайова задача — задача теорії диференціальних рівнянь , в якій межові умови задаються в різних точках. Наприклад, при коливаннях струни із закріпленеми кінцями зміщення на кожному з кінців дорівнює нулю.
Крайові задачі складніше розв'язувати, ніж задачі Коші , особливо чисельно.
Крайові задачі виникають як у теорії звичайних диференціальних рівнянь , так і в теорії диференціальних рівнянь з частинними похідними , особливо рівнянь еліптичного типу .
Особливий вид крайової задачі — вимога певної поведінки функції (скінченності) при прямуванні аргументу до нескінченності або в околі особливих точок.
Нехай
Ω
{\displaystyle \Omega }
x
,
y
{\displaystyle x,y}
Γ
.
{\displaystyle \Gamma .}
Важливими задачами є:
u
(
x
,
y
)
|
(
x
,
y
)
∈
Γ
=
φ
(
x
,
y
)
{\displaystyle u(x,y)|_{(x,y)\in \Gamma }=\varphi (x,y)}
задача Діріхле
∂
u
(
x
,
y
)
∂
n
|
(
x
,
y
)
∈
Γ
=
φ
(
x
,
y
)
=
ψ
(
x
,
y
)
{\displaystyle {\frac {\partial u(x,y)}{\partial n}}\vert _{(x,y)\in \Gamma }=\varphi (x,y)=\psi (x,y)}
задача Неймана
a
u
(
x
,
y
)
+
b
∂
u
(
x
,
y
)
∂
n
=
χ
(
x
,
y
)
{\displaystyle au(x,y)+b{\frac {\partial u(x,y)}{\partial n}}=\chi (x,y)}
(
x
,
y
)
{\displaystyle (x,y)}
Γ
{\displaystyle \Gamma }
задача Робена Розглядається не континуум точок площини
x
,
y
,
{\displaystyle x,y,}
Π
i
j
=
(
x
i
,
y
i
)
.
{\displaystyle \Pi _{ij}=(x_{i},y_{i}).}
Якщо область
Ω
{\displaystyle \Omega }
Ω
∗
{\displaystyle \Omega ^{*}}
Ω
{\displaystyle \Omega }
Γ
∗
.
{\displaystyle \Gamma ^{*}.}
Ω
~
∗
=
Ω
∗
⋃
Γ
{\displaystyle {\tilde {\Omega }}^{*}=\Omega ^{*}\bigcup \Gamma }
Друга можливість полягає в тому, що додають точки перетину
Γ
{\displaystyle \Gamma }
Похідні, які зустрічаються у розглядуваному диференціальному рівнянні, замінюють у кожній точці сітки
Π
i
j
=
(
x
i
,
y
i
)
{\displaystyle \Pi _{ij}=(x_{i},y_{i})}
∂
u
∂
n
|
i
j
=
1
2
h
(
−
u
i
−
1
,
j
+
u
i
+
1
,
j
)
+
O
(
h
2
)
.
{\displaystyle {\frac {\partial u}{\partial n}}\vert _{ij}={\frac {1}{2h}}(-u_{i-1,j}+u_{i+1,j})+O(h^{2}).}
Такі вирази називають також молекулами й записують у вигляді наочних структурних формул.
П'ятиточкові молекули для оператора Лапласа (квадратна сітка):
Якщо область
Ω
{\displaystyle \Omega }
Γ
{\displaystyle \Gamma }
Наприклад, рівняння Пуассона у прямокутнику[ 1]
Ω
=
{
(
x
,
y
)
|
0
≤
x
≤
4
k
,
0
≤
y
≤
3
h
}
.
{\displaystyle \Omega =\{(x,y)|0\leq x\leq 4k,\,\,0\leq y\leq 3h\}.}
Сітка
(
x
i
,
y
i
)
=
(
i
k
,
j
h
)
,
{\displaystyle (x_{i},y_{i})=(ik,jh),}
Ω
∗
=
{
(
i
k
,
j
h
)
|
0
≤
i
≤
4
,
4
≤
j
≤
3
}
{\displaystyle \Omega ^{*}=\{(ik,jh)|0\leq i\leq 4,\,\,4\leq j\leq 3\}}
Нехай
Ω
{\displaystyle \Omega }
x
,
y
{\displaystyle x,y}
Γ
.
{\displaystyle \Gamma .}
u
(
x
,
y
)
,
{\displaystyle u(x,y),}
Ω
{\displaystyle \Omega }
Δ
u
=
u
x
x
′
′
+
u
y
y
′
′
=
g
(
x
,
y
)
.
{\displaystyle \Delta u=u_{xx}^{\prime \prime }+u_{yy}^{\prime \prime }=g(x,y).}
При застосуванні молекули ліворуч
U
i
−
1
,
j
+
U
i
+
1
,
j
+
U
i
,
j
−
1
+
U
i
,
j
+
1
−
4
U
i
j
=
h
2
f
i
j
{\displaystyle U_{i-1,j}+U_{i+1,j}+U_{i,j-1}+U_{i,j+1}-4U_{ij}=h^{2}f_{ij}}
як дискретний аналог рівняння Пуассона (через
U
i
j
{\displaystyle U_{ij}}
u
(
x
i
,
y
j
)
=
u
i
j
{\displaystyle u(x_{i},y_{j})=u_{ij}}
Якщо записати усі рівняння, для яких «центральний елемент»
u
i
j
{\displaystyle u_{ij}}
1
≤
i
≤
3
,
1
≤
j
≤
2
{\displaystyle 1\leq i\leq 3,\,\,1\leq j\leq 2}
U
01
_
+
U
21
+
U
10
_
+
U
12
−
4
U
11
=
h
2
f
11
{\displaystyle {\underline {U_{01}}}+U_{21}+{\underline {U_{10}}}+U_{12}-4U_{11}=h^{2}f_{11}}
U
11
+
U
31
+
U
20
_
+
U
22
−
4
U
21
=
h
2
f
21
{\displaystyle U_{11}+U_{31}+{\underline {U_{20}}}+U_{22}-4U_{21}=h^{2}f_{21}}
U
21
+
U
41
_
+
U
30
_
+
U
32
−
4
U
31
=
h
2
f
31
{\displaystyle U_{21}+{\underline {U_{41}}}+{\underline {U_{30}}}+U_{32}-4U_{31}=h^{2}f_{31}}
U
02
_
+
U
22
+
U
10
+
U
13
_
−
4
U
12
=
h
2
f
12
{\displaystyle {\underline {U_{02}}}+U_{22}+U_{10}+{\underline {U_{13}}}-4U_{12}=h^{2}f_{12}}
U
12
+
U
32
+
U
20
+
U
23
_
−
4
U
22
=
h
2
f
22
{\displaystyle U_{12}+U_{32}+U_{20}+{\underline {U_{23}}}-4U_{22}=h^{2}f_{22}}
U
22
+
U
42
_
+
U
30
+
U
33
_
−
4
U
32
=
h
2
f
32
{\displaystyle U_{22}+{\underline {U_{42}}}+U_{30}+{\underline {U_{33}}}-4U_{32}=h^{2}f_{32}}
Підкреслені значення можна перенести праворуч.
Тоді дискретним аналогом задачі є система лінійних рівнянь:
(
−
4
1
0
1
0
0
1
−
4
1
0
1
0
0
1
−
4
0
0
1
1
0
0
−
4
1
0
0
1
0
1
−
4
1
0
0
1
0
1
−
4
)
(
U
11
U
21
U
31
U
12
U
22
U
32
)
=
(
h
11
2
−
U
01
−
U
10
h
2
f
21
−
U
20
h
2
f
31
−
U
41
−
U
30
h
2
f
12
−
U
02
−
U
13
h
2
f
22
−
U
23
h
2
f
32
−
U
42
−
U
33
)
.
{\displaystyle {\begin{pmatrix}-4&1&0&1&0&0\\1&-4&1&0&1&0\\0&1&-4&0&0&1\\1&0&0&-4&1&0\\0&1&0&1&-4&1\\0&0&1&0&1&-4\end{pmatrix}}{\begin{pmatrix}U_{11}\\U_{21}\\U_{31}\\U_{12}\\U_{22}\\U_{32}\end{pmatrix}}={\begin{pmatrix}h_{11}^{2}-U_{01}-U_{10}\\h^{2}f_{21}-U_{20}\\h^{2}f_{31}-U_{41}-U_{30}\\h^{2}f_{12}-U_{02}-U_{13}\\h^{2}f_{22}-U_{23}\\h^{2}f_{32}-U_{42}-U_{33}\end{pmatrix}}.}
Для розв'язання таких систем застосовують ітераційні методи, хоча можуть застосовуватися методи, які використовують блокову структуру.
↑ Е. А. Волков, О решении краевых задач для уравнения Пуассона в прямоугольнике, Докл. АН СССР, 1962, том 147, номер 1, 13–16 .