Круговий трикутник

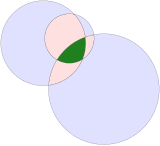Опуклий круговий трикутник	Впуклий круговий трикутник

Круговим трикутником в еквклідовій геометрії називають трикутник, у якого сторонами є дуги кола.

Побудова

Особливі випадки
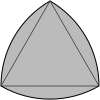Трикутник Рело	Арбелос

Опуклий круговий трикутник може бути побудований за допомогою перетину трьох кругових дисків. Його краї всі загнуті назовні. Сума внутрішніх кутів кругового трикутника більша за 180°. Трикутник Рело — це окремий випадок рівностороннього трикутника, де центр кожної дуги знаходиться в протилежній вершині трикутника.

Круговий увігнутий трикутник є подібним поняттям, але представляє ділянку, яка розташована всередині 3 взаємно дотичних кіл, тому всі його внутрішні кути дорівнюють нулю. ^[1] Арбелос є окремим випадком в якому всі три вершини є колінеарними, тобто, вони розташовані на одній прямій, та трьома ребрами кожне з яких є півколом.^[2]

Інші кругові трикутники можуть мати різні поєднання опуклих і увігнутих ребер дуги кола:

Довгі дуги можуть створювати увігнуті фігури незалежно від того, вигнуті окремі краї всередину чи назовні. Вигнуті всередину дуги можуть створювати форми, що перетинаються між собою, наприклад фігуру трикветра:

Теселяції

Кругові трикутрики утворюються при теселяції.

Див. також

Гіперболічний трикутник – трикутник, який має прямі сторони в гіперболічній геометрії, але зображується за допомогою кіл в деяких моделях гіперболічної геометрії. Зокрема у конформно-евклідовій моделі
Місяць^[en] та лінза^[en] — кругові двокутники

Примітки

↑ The Geometry of the Circular Horn Triangle Edward Kasner and Aida Kalish National Mathematics Magazine Vol. 18, No. 8 (May, 1944), pp. 299–304
↑ Boas, Harold P. (2006), Reflections on the arbelos (PDF), American Mathematical Monthly, 113 (3): 236—249, doi:10.2307/27641891, JSTOR 27641891, MR 2204487, архів оригіналу (PDF) за 28 березня 2022, процитовано 27 січня 2023.

Курант Р., Роббінс Г. Що таке математика?. — 3-є. — Москва : МЦНМО, 2001. — 568 с.(рос.)

Посилання

Weisstein, Eric W. Reuleaux Triangle(англ.) на сайті Wolfram MathWorld.
Weisstein, Eric W. Circular Triangle(англ.) на сайті Wolfram MathWorld.
Weisstein, Eric W. Arbelos(англ.) на сайті Wolfram MathWorld.

Це незавершена стаття з геометрії.
Ви можете допомогти проєкту, виправивши або дописавши її.

[1] The Geometry of the Circular Horn Triangle Edward Kasner and Aida Kalish National Mathematics Magazine Vol. 18, No. 8 (May, 1944), pp. 299–304

[2] Boas, Harold P. (2006), Reflections on the arbelos (PDF), American Mathematical Monthly, 113 (3): 236—249, doi:10.2307/27641891, JSTOR 27641891, MR 2204487, архів оригіналу (PDF) за 28 березня 2022, процитовано 27 січня 2023.

[1]

[2]