Політ Леві

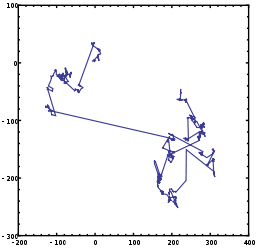
Політ Леві (названий на честь французького математика Поля Леві) — випадкове блукання, у якому довжини кроку мають розподіл Леві, тобто розподіл імовірностей з важким хвостом. Кроки виконуються в ізотропних випадкових напрямках.

Термін «політ Леві» запропонував Бенуа Мандельброт, який використовував його для одного конкретного визначення розподілу розмірів кроку. Він використовував термін політ Коші для випадку, коли розподіл розмірів кроку є розподілом Коші, і політ Релея для нормального розподілу розмірів кроку (який не є прикладом розподілу ймовірностей з важким хвостом).

Пізніше дослідники розширили використання терміна «політ Леві», включивши в нього випадки, коли випадкове блукання відбувається на дискретній сітці, а не в безперервному просторі.

Рис. 1. Приклад 1000 кроків польоту Леві в двох вимірах. Початок руху знаходиться в точці [0,0], кутовий напрямок розподілено рівномірно, а розмір кроку розподілений згідно з розподілом Леві (тобто стабільний) з α = 1 і β = 0. Зверніть увагу на наявність великих стрибків в місці розташування в порівнянні з броунівським рухом, показаним на рис. 2.

Рис. 2. Приклад тисячі кроків наближення до типу броунівського руху польоту Леві в двох вимірах. Початок руху знаходиться в точці [0, 0], кутовий напрямок розподілено рівномірно, а розмір кроку розподілений згідно з розподілом Леві (тобто стабільний) з α = 2 і β = 0 (тобто, нормальний розподіл).

Література

• Viswanathan, G.; Bartumeus, F.; v. Buldyrev, S.; Catalan, J.; Fulco, U.; Havlin, S.; Da Luz, M.; Lyra, M.; Raposo, E.; Eugene Stanley, H. (2002). Lévy flight random searches in biological phenomena. Physica A: Statistical Mechanics and Its Applications. 314 (1–4): 208—213. Bibcode:2002PhyA..314..208V. doi:10.1016/S0378-4371(02)01157-3.
• Viswanathan, G.; Afanasyev, V.; Buldyrev, S.; Havlin, S.; Daluz, M.; Raposo, E.; Stanley, H. (2000). Lévy flights in random searches. Physica A: Statistical Mechanics and Its Applications. 282 (1–2): 1—12. Bibcode:2000PhyA..282....1V. doi:10.1016/S0378-4371(00)00071-6.
• Cheng, Z.; Savit, R. (1987). Fractal and nonfractal behavior in Levy flights (PDF). Journal of Mathematical Physics. 28 (3): 592. Bibcode:1987JMP....28..592C. doi:10.1063/1.527644. hdl:2027.42/70735.
• Shlesinger, Michael F.; Klafter, Joseph; Zumofen, Gert (December 1999). Above, below and beyond Brownian motion (PDF). American Journal of Physics. 67 (12): 1253—1259. Bibcode:1999AmJPh..67.1253S. doi:10.1119/1.19112. Архів оригіналу (PDF) за 28 березня 2012.

Інтернет-ресурси

• A comparison of the paintings of Jackson Pollock to a Lévy flight model [Архівовано 15 червня 2010 у Wayback Machine.]