Послідовність «подивися-і-скажи»

Графіки показують зростання кількості цифр у послідовності «подивися-і-скажи» з початковими числами: 1 (синій), 13 (фіолетовий), 23 (червоний) та 312 (зелений). Ці графіки прямують до прямих ліній (вертикальна вісь має логарифмічний масштаб)

Послідовність «подивися-і-скажи» — це послідовність чисел, що починається так:

1, 11, 21, 1211, 111221, 312211, 13112221, 1113213211, … (послідовність A005150 в OEIS).

Кожне наступне число будується за попереднім послідовним записом для кожної групи однакових цифр кількості цифр у цій групі та самої цифри, з якої складається група. Наприклад:

• 1 читається як «одна одиниця», тобто 11
• 11 читається як «дві одиниці», тобто 21
• 21 читається як «одна двійка, одна одиниця», тобто 1211
• 1211 читається як «одна одиниця, одна двійка, дві одиниці», тобто 111221
• 111221 читається як «три одиниці, дві двійки, одна одиниця», тобто 312211
• 312211 читається як «одна трійка, одна одиниця, дві двійки, дві одиниці», тобто 13112221

Послідовність «подивися-і-скажи» запропонував Джон Конвей.

Для довільної початкової цифри d, крім одиниці, послідовність набуває вигляду:

d, 1d, 111d, 311d, 13211d, 111312211d, 31131122211d, …

Основні властивості

Коріння багаточлена Конвея на комплексній площині

Зростання

Послідовність зростає нескінченно. Фактично, будь-який варіант послідовності з цілим початковим числом зростатиме нескінченно. Виняток становить послідовність:

22, 22, 22, 22, 22, … (послідовність A010861 в OEIS).

Обмеження цифр, що використовуються

Жодні цифри, крім 1, 2 і 3 не зустрічаються в послідовності, якщо початкове число не містить інших цифр або групи з більш ніж трьох цифр.

Зростання довжини чисел

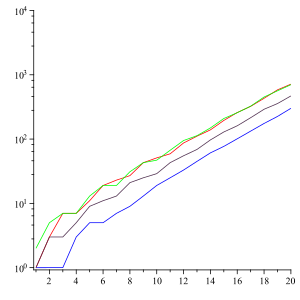
У середньому числа виростають на 30 % за ітерацію. Якщо $L_{n}$ позначає довжину n-го члена послідовності, то існує границя відношення ${\frac {L_{n+1}}{L_{n}}}$ :

$\lim _{n\to \infty }{\frac {L_{n+1}}{L_{n}}}=\lambda$.

Тут λ = 1.303577269034 … — стала Конвея. Цей результат справедливий для будь-якого варіанту послідовності з початковим числом, відмінним від 22.

Многочлен, який повертає сталу Конвея

Стала Конвея — це єдиний додатний дійсний корінь многочлена:

${\begin{aligned}&\,\,\,\,\,\,\,x^{71}&&&&-x^{69}&&-2x^{68}&&-x^{67}&&+2x^{66}&&+2x^{65}&&+x^{64}&&-x^{63}\\&-x^{62}&&-x^{61}&&-x^{60}&&-x^{59}&&+2x^{58}&&+5x^{57}&&+3x^{56}&&-2x^{55}&&-10x^{54}\\&-3x^{53}&&-2x^{52}&&+6x^{51}&&+6x^{50}&&+x^{49}&&+9x^{48}&&-3x^{47}&&-7x^{46}&&-8x^{45}\\&-8x^{44}&&+10x^{43}&&+6x^{42}&&+8x^{41}&&-5x^{40}&&-12x^{39}&&+7x^{38}&&-7x^{37}&&+7x^{36}\\&+x^{35}&&-3x^{34}&&+10x^{33}&&+x^{32}&&-6x^{31}&&-2x^{30}&&-10x^{29}&&-3x^{28}&&+2x^{27}\\&+9x^{26}&&-3x^{25}&&+14x^{24}&&-8x^{23}&&&&-7x^{21}&&+9x^{20}&&+3x^{19}&&-4x^{18}\\&-10x^{17}&&-7x^{16}&&+12x^{15}&&+7x^{14}&&+2x^{13}&&-12x^{12}&&-4x^{11}&&-2x^{10}&&+5x^{9}\\&&&+x^{7}&&-7x^{6}&&+7x^{5}&&-4x^{4}&&+12x^{3}&&-6x^{2}&&+3x&&-6\end{aligned}}$

У своїй оригінальній статті Конвей помилково написав «−» замість «+» перед $x^{35}$. Але значення λ, наведене в його статті, правильне.

Популяризація

Послідовність «подивися-і-скажи» також відома як послідовність чисел Морріса на честь криптографа Роберта Морріса. Іноді її називають «зозулине яйце» через головоломку «Яке наступне число в послідовності 1, 11, 21, 1211, 111221?», за описом Морріса в книзі Кліффорда Столла «Зозулине яйце».

Варіації

Існує багато варіантів правил для створення послідовностей, подібних до «подивися-і-скажи». Наприклад, послідовність «pea pattern». Вона відрізняється від «подивися-і-скажи» тим, що для отримання нового числа в ній потрібно підраховувати всі однакові цифри в числі. Починаючи з числа 1, отримаємо: 1, 11 (одна одиниця), 21 (дві одиниці), 1211 (одна двійка, одна одиниця), 3112 (три одиниці, одна двійка), 132112 (одна трійка, дві одиниці, одна двійка), 312213 (три одиниці, дві двійки, одна трійка) і т. д. Зрештою послідовність приходить до циклу з двох чисел, 23322114 і 32232114.

Існує інший варіант, який відрізняється від «pea pattern» тим, що цифри підраховуються в порядку зростання, а не в міру появи. Починаючи з одиниці, отримаємо послідовність: 1, 11, 21, 1112, 3112, 211213, 312213, …

Ці послідовності мають цікаві відмінності від «подивися-і-скажи». На відміну від послідовності Конвея, кожен член у «pea pattern» не однозначно визначає попередній член. Довжина чисел у «pea pattern» обмежена і, для b-кової системи числення, не перевищує 2b, і досягає 3b для великих початкових чисел (наприклад, «сто одиниць»).

Оскільки ця послідовність нескінченна і довжина її члена обмежена, вона, за принципом Диріхле, повинна зрештою повторитися. Як наслідок, ці послідовності завжди періодичні.