Стягування ребра
В теорії графів стягування ребра — це операція, яка видаляє ребро з графу, а до цього зв'язані ребром вершини зливаються в одну вершину. Стягування ребра є фундаментальною операцією в теорії про мінори графів. Ототожнення вершин — інша форма цієї операції зі слабшими обмеженнями.
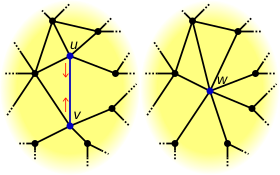
Операція стягування ребра виконується над конкретним ребром e. Ребро e видаляється, а дві інцидентні йому вершини u і v, зливаються в нову вершину w, де ребра, інцидентні w, відповідають ребрам, інцидентним або u або v. Загальніше, операцію можна провести на множині ребер шляхом стягування ребер із множини (в будь-якому порядку)[1].
Як визначено нижче, операція стягування ребра може дати граф із кратними ребрами навіть якщо початковий граф був простим графом[2]. Однак деякі автори[3] не дозволяють створення кратних ребер, так що стягування ребер на простому графі завжди дають прості графи.
Нехай G=(V,E) — граф (чи орієнтований граф), що містить ребро e=(u,v) з u≠v. Нехай f — функція, яка відображає будь-яку вершину в V\{u,v} в себе, а в іншому випадку — у вершину w. Стягування e призводить до нового графу G'=(V',E'), де V'=(V\{u,v})∪{w}, E'=E\{e}, і для будь-якої вершини x∈V, вершина x'=f(x)∈V' інцидентна ребру e'∈E' тоді й лише тоді, коли відповідне ребро e∈E інцидентне x у G.
Ототожнення вершин (іноді називається стягуванням вершин) не використовує обмеження, що стягування повинне проводитися з вершинами, інцидентними одному ребру (таким чином, стягання ребра є частковим випадком ототожнення вершин). Цю операцію можна провести з будь-якою парою (або підмножиною) вершин у графі. Ребра між двома стягуваними вершинами іноді видаляються. Якщо v і v' — вершини різних компонент графу G, то ми можемо створити новий граф G' через ототожнення v і v' в G в нову вершину v в G'[4].
Розщеплення вершин означає заміну однієї вершини двома, і ці дві нові вершини суміжні вершинам, яким була суміжна початкова вершина. Операція є оберненою ототожненню вершин.
Стягування шляху здійснюється з множиною ребер у шляху, які стягуються, утворюючи одне ребро між кінцевими вершинами шляху. Ребра, інцидентні вершинам уздовж шляху, або відкидаються, або випадковим чином (чи за певною системою) з'єднуються з однією з кінцевих вершин.
Нехай дано два графи G1 і G2, що не перетинаються, де G1 містить вершини u1 і v1, а G2 містить вершини u2 v2. Припустимо, що ми отримали граф G шляхом ототожнення вершин u1 графу G1 і u2 графу G2, отримавши вершину u в G, і ототожнення вершин v1 графу G1 і v2 графу G2, отримавши вершину v в G. В скручуванні G' графу G відносно пари вершин {u, v}, ми ототожнюємо замість зазначених вище вершини u1 з v2 і v1 з u2[5].
Як стягування ребра, так і стягування вершин мають важливе значення для доведення за математичною індукцією за кількістю вершин або ребер графу, де можна припустити, що властивість виконується для всіх менших графів і це можна використати для доведення властивостей великих графів.
Стягування ребра використовується в рекурсивній формулі числа стягувальних дерев довільного зв'язного графу[1] і в рекурентній формулі для хроматичного полінома простого графу[6].
Стягування також корисне в структурах, де потрібно спростити граф шляхом ототожнення вершин, які представляють істотно еквівалентні об'єкти. Найвідомішим прикладом є зведення загального орієнтованого графу до орієнтованого ациклічного графу стягуванням усіх вершин у кожній компоненті сильної зв'язності. Якщо відношення, описуване графом є транзитивним, ніяка інформація не втрачається, якщо позначити кожну вершину множиною позначок вершин, які стягнуто в цю вершину.
Інший приклад — злиття, проведене в розфарбуванні графу при глобальному розподілі регістрів, де вершини зливаються (де можна) для виключення операцій переміщення даних між різними змінними.
Стягування ребра використовується в пакунках тривимірного моделювання (або вручну, або за допомогою моделювальних програм) для послідовного скорочення числа вершин з метою створення моделей у вигляді багатокутників з малим числом сторін.
- ↑ а б Gross, Yellen, 1998, с. 264.
- ↑ Можуть також з'явитися петлі, якщо початковий граф мав кратні ребра. Петлі можуть з'явитися і з простого графу, якщо стягнути декілька ребер.
- ↑ Rosen, 2011, с. 664.
- ↑ Oxley, 1992, с. 147—148.
- ↑ Oxley, 1992, с. 148.
- ↑ West, 2001, с. 221.
- Jonathan Gross, Jay Yellen. Graph Theory and its applications. — CRC Press, 1998. — ISBN 0-8493-3982-0.
- James Oxley. Matroid Theory. — Oxford University Press, 1992.
- Kenneth Rosen. Discrete Mathematics and Its Applications. — 7th. — McGraw-Hill, 2011. — ISBN 9780073383095.
- Douglas B. West. Introduction to Graph Theory. — 2nd. — Prentice-Hall, 2001. — ISBN 0-13-014400-2.
- Weisstein, Eric W. Edge Contraction(англ.) на сайті Wolfram MathWorld.
