Теорема Морлі

Трикутник Морлея

Теорема Морлі про трисектриси трикутника — одна з найдивовижніших теорем геометрії трикутника.

Теорема стверджує:

Точки перетину суміжних трисектрис внутрішніх кутів довільного трикутника є вершинами рівностороннього трикутника.

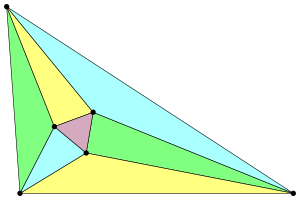
На рисунку праворуч три різнокольорових кута при кожній вершині великого трикутника рівні між собою. Теорема стверджує, що незалежно від вибору великого трикутника, маленький фіолетовий трикутник буде рівностороннім.

Теорема Морлі не виконується в сферичній і гіперболічній геометрії.

Терема Морлі для трисектрис зовнішніх кутів трикутника

Теорема Морлі для трисектрис зовнішніх кутів трикутника

Теорема також справедлива для зовнішніх кутів трикутника:

Точки перетину суміжних трисектрис зовнішніх кутів довільного трикутника є вершинами рівносторонніх трикутників.

Крім того продовження трисектрис внутрішніх кутів також перетинаються з суміжними трисектрисами зовнішніх кутів у вершинах цих трикутників.

Історія

Теорема була відкрита в 1904 Франком Морлі. Тоді він розповів про неї друзям з Кембриджського університету, а опублікував її в 1924 році, коли він був у Японії.. За цей час вона була незалежно опублікована як задача в часописі «Educational Times».

Доведення

Існує багато способів доведення теореми Морлі, деякі з яких дуже технічні.

Кілька ранніх доведень ґрунтувалися на тригонометричних розрахунках. До одних з крайніх доведень теореми належать алгебричне доведення Алена Конна (1998, 2004), яке поширює теорему на загальні поля, окрім тих що мають характеристику три, і доведення Джона Конвея, що спирається на елементарну геометрію . Останній починається з рівностороннього трикутника і показує, що навколо нього можна побудувати трикутник, подібний до будь-якого обраного трикутника.

Доведення  

Доведення теореми Морлі

Для доведення використаємо тригонометричну тотожність:

$\sin(3\varphi )=4\sin \varphi \cdot \sin(60^{\circ }+\varphi )\cdot \sin(120^{\circ }+\varphi )$

(1)

Точки $D,E,F$ побудовані на стороні $BC$ як показано на малюнку.

Сума внутрішніх кутів трикутника = 180^o, а значить:$3\alpha +3\beta +3\gamma =180^{\circ }$,

Отже, $\alpha +\beta +\gamma =60^{\circ }.$

Кути трикутника $XEF$ дорівнюють: $\alpha ,(60^{\circ }+\beta )$ та $(60^{\circ }+\gamma ).$

З прямокутних трикутників, маємо:

$\sin(60^{\circ }+\beta )={\frac {DX}{XE}}$

(2)

а також:

$\sin(60^{\circ }+\gamma )={\frac {DX}{XF}}.$

(3)

Далі:

$\angle {AYC}=180^{\circ }-\alpha -\gamma =120^{\circ }+\beta$

аналогічно і

$\angle {AZB}=120^{\circ }+\gamma .$

(4)

Застосовуємо теорему синусів для трикутників $AYC$ та $AZB$ :

$\sin(120^{\circ }+\beta )={\frac {AC}{AY}}\sin \gamma$

(5)

$\sin(120^{\circ }+\gamma )={\frac {AB}{AZ}}\sin \beta .$

(6)

Висоту трикутника $ABC$ знаходимо двома способами:

$h=AB\cdot \sin(3\beta )=AB\cdot 4\sin \beta \sin(60^{\circ }+\beta )\sin(120^{\circ }+\beta )$

та

$h=AC\cdot \sin(3\gamma )=AC\cdot 4\sin \gamma \sin(60^{\circ }+\gamma )\sin(120^{\circ }+\gamma ).$

Підставляємо замість синусів їх значення з рівнянь (2) та (5), а також (3) та (6). Отримуємо:

$h=4AB\cdot \sin \beta \cdot {\frac {DX}{XE}}\cdot {\frac {AC}{AY}}\cdot \sin \gamma$

та

$h=4AC\cdot \sin \gamma \cdot {\frac {DX}{XF}}\cdot {\frac {AB}{AZ}}\cdot \sin \beta$

Оскільки чисельники в обох виразах рівні, то: $XE\cdot AY=XF\cdot AZ$

або: ${\frac {XE}{XF}}={\frac {AZ}{AY}}.$

Оскільки $\measuredangle EXF=\measuredangle ZAY$, а сторони, що утворюють ці кути, знаходяться в однаковому співвідношенні, то трикутники $XEF$ та $AZY$ подібні. Відповідні кути $\measuredangle AYZ$ та $\measuredangle XFE$ рівні $(60^{\circ }+\gamma )$, а кути $\measuredangle AZY$ та $\measuredangle XEF$ рівні $(60^{\circ }+\beta ).$ Рівні також і відповідні кути при основі трикутників $BXZ$ та $CYX.$Зокрема $\measuredangle BZX=(60^{\circ }+\alpha )$ і з малюнка можемо бачити, що:

$\angle {AZY}+\angle {AZB}+\angle {BZX}+\angle {XZY}=360^{\circ }.$

Підставляємо їх значення (кут $AZB$ беремо з рівняння (4)): $(60^{\circ }+\beta )+(120^{\circ }+\gamma )+(60^{\circ }+\alpha )+\angle {XZY}=360^{\circ }$

Звідки отримуємо: $\angle {XZY}=60^{\circ }.$

Аналогічно знаходимо, що і іншу кути трикутника $XYZ$ рівні $60^{\circ }.$ Теорему доведено.

Трикутники Морлі

Теорема Морлі містить 18 спеціальних трикутників (рівносторонніх і різносторонніх), які виникають при перетині трисектрис трикутника.

Правильний трикутник, описаний вище в теоремі про трисектриси внутрішніх кутів, називається першим трикутником Морлі, і має довжину сторони:

$a^{\prime }=8R\sin(A/3)\sin(B/3)\sin(C/3),\,$

та площу:

$S={\tfrac {\sqrt {3}}{4}}a'^{2}=16{\sqrt {3}}R^{2}\sin ^{2}(A/3)\sin ^{2}(B/3)\sin ^{2}(C/3).$

де R — радіус описаного кола початкового трикутника, а A, B та C — його внутрішні кути.

З першим трикутником Морлі також пов'язані дві чудові точки трикутника — перша та друга точки Морлі, які в Енциклопедії центрів трикутника ETC Кларка Кімберлінга мають номери X(356) та X(357).

Див. також

• Трисекція кута — задача про побудову трисектрис кута за допомогою циркуля та лінійки
• Трисектриса

Джерела

1. H. S. M. Coxeter, Samuel L.Greitzer. ""Morley's Theorem." §2.9 in Geometry Revisited.. — Washington, DC: Math. Assoc. Amer., 1967. — Vol. 19. — P. 193: 47-50.
2. Wells, D. (1991). The Penguin Dictionary of Curious and Interesting Geometry (PDF) (англ.). London: Penguin. с. 154—155. ISBN 0-14-011813-6.
3. Child, J. M. "Proof of Morley's Theorem.". — Math. Gaz., 1923. — No. 11. — P. 171.
4. Taylor, F. G. and Marr, W. L. "The six trisectors of each of the angles of a triangle" // Proceedings of the Edinburgh Mathematical Society. — 1913–14. — No. 33. — P. 119–131. — DOI:10.1017/S0013091500035100.

Посилання

• Weisstein, Eric W. Morley's Theorem(англ.) на сайті Wolfram MathWorld.
• Morley's Trisection Theorem на MathPages