Теорема про три геодезичні
У диференціальній геометрії теорема про три геодезичні стверджує, що кожен ріманів многовид з топологією сфери має три замкнені геодезичні, які є простими замкненими кривими без самоперетинів.[1][2] Теорема також буде вірною для випадку квазігеодезичних ліній на поверхні опуклого багатогранника.
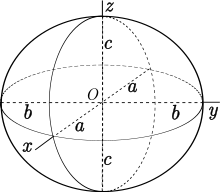
Виникнення теореми пов'язане із математикою навігації в океані, де поверхня Землі може бути точно змодельована за допомогою еліпсоїда, а також у зв'язку з вивченням геодезичних на еліпсоїді[en]. Зокрема, тривісний еліпсоїд має тільки три прості замкнуті геодезичні що є його екваторами.[3] У 1905 році Анрі Пуанкаре висловив гіпотезу, що будь-яка гладка поверхня, що топологічно еквівалентна сфері аналогічним чином містить щонайменше три прості замкнені геодезичні[4], а в 1929 р Люстерник і Шнирельман опублікували доказ гіпотези в якому пізніше були знайдені недоліки.[5] В одному з доказів цієї гіпотези розглядаються гомології простору гладких кривих на сфері та вкорочувальний потік з метою знайдення простої замкненої геодезичної, що представляє кожен з трьох нетривіальних класів гомології цього простору.[2]
На додаток, обов'язково існують три прості замкнені геодезичні, довжина яких найбільш пропорційна діаметру поверхні.[6]
Кількість замкнених геодезичних довжин щонайбільше L на гладкій топологічній сфері зростає пропорційно L/log L, але не можна гарантувати, що такі геодезичні будуть простими.[7]
На компактних гіперболічних ріманових поверхнях існує нескінченно багато простих замкнених геодезичних, але якщо накласти обмеження, щоб довжина не перевищувала задане число, то таких кривих буде скінченна кількість. Вони аналітично задаються за допомогою дзета-функції Сельберга[en]. Оцінки швидкості зростання кількості простих замкнених геодезичних, як функції їх довжини, досліджувала Мар'ям Мірзахані.[8]
Існування трьох простих замкнених геодезичних також має місце для будь-якої оберненої фінслерової метрики на 2-сфері.[9]
| Нерозв'язана проблема математики: Чи існує алгоритм знаходження простої квазігеодезичної на опуклому многогранику за поліноміальний час? (більше нерозв'язаних проблем математики)
|
Можна визначити геодезичну на деякій поверхні, що не є всюди гладкою, така, як опуклий багатогранник. Однак, деякі багатогранники мають прості замкнені геодезичні, (наприклад тетраедр та рівнограний тетраедр[en] мають нескінченно багато простих замкнених геодезичних)[10][11] інші не мають. Зокрема, проста замкнена геодезична на опуклому багатограннику обов'язково буде ділити навпіл сумарний дефект вершин, та для майже всіх багатогранників це не буде вірно.[3][10]
Проте, теорему про три геодезичні можна поширити на випадок квазігеодезичних на опуклому багатограннику. Тобто, будь-який багатогранник має хоча б три прості замкнені квазігеодезичні, що можна довести шляхом наближення багатогранника до гладкої поверхні після чого застосувати теорему про три геодезичні.[12] Можливість побудови квазігеодезичної на опуклому багатограннику за поліноміальний час є відкритим питанням.
- ↑ Klingenberg, Wilhelm (1985), The existence of three short closed geodesics, Differential geometry and complex analysis, Springer, Berlin, с. 169—179, MR 0780043, архів оригіналу за 20 травня 2016, процитовано 26 серпня 2016.
- ↑ а б Grayson, Matthew A. (1989), Shortening embedded curves (PDF), Annals of Mathematics, Second Series, 129 (1): 71—111, doi:10.2307/1971486, MR 0979601.
- ↑ а б Galperin, G. (2003), Convex polyhedra without simple closed geodesics (PDF), Regular & Chaotic Dynamics, 8 (1): 45—58, doi:10.1070/RD2003v008n01ABEH000231, MR 1963967, архів оригіналу (PDF) за 22 січня 2022, процитовано 26 серпня 2016.
- ↑ Poincaré, H. (1905), Sur les lignes géodésiques des surfaces convexes [Geodesics lines on convex surfaces], Transactions of the American Mathematical Society (French) , 6 (3): 237—274, doi:10.2307/1986219, JSTOR 1986219, архів оригіналу за 12 квітня 2016, процитовано 26 серпня 2016.
- ↑ Lyusternik, L.; Schnirelmann, L. (1929), Sur le problème de trois géodésiques fermées sur les surfaces de genre 0 [The problem of three closed geodesics on surfaces of genus 0], Comptes Rendus de l'Académie des Sciences de Paris (French) , 189: 269—271.
- ↑ Liokumovich, Yevgeny; Nabutovsky, Alexander; Rotman, Regina (2014), Lengths of three simple periodic geodesics on a Riemannian 2-sphere, arXiv:1410.8456.
- ↑ Hingston, Nancy (1993), On the growth of the number of closed geodesics on the two-sphere, International Mathematics Research Notices (9): 253—262, doi:10.1155/S1073792893000285, MR 1240637
{{citation}}: Обслуговування CS1: Сторінки із непозначеним DOI з безкоштовним доступом (посилання). - ↑ Mirzakhani, Maryam (2008), Growth of the number of simple closed geodesics on hyperbolic surfaces, Annals of Mathematics, 168 (1): 97—125, doi:10.4007/annals.2008.168.97, MR 2415399, Zbl 1177.37036,
- ↑ De Philippis, Guido; Marini, Michele; Mazzucchelli, Marco; Suhr, Stefan (2022), Closed geodesics on reversible Finsler 2-spheres, Journal of Fixed Point Theory and Applications, 24 (2), arXiv:2002.00415, doi:10.1007/s11784-022-00962-9.
- ↑ а б Fuchs, Dmitry; Fuchs, Ekaterina (2007), Closed geodesics on regular polyhedra (PDF), Moscow Mathematical Journal, 7 (2): 265—279, 350, MR 2337883, архів оригіналу (PDF) за 19 січня 2017, процитовано 26 серпня 2016.
- ↑ Cotton, Andrew; Freeman, David; Gnepp, Andrei; Ng, Ting; Spivack, John; Yoder, Cara (2005), The isoperimetric problem on some singular surfaces, Journal of the Australian Mathematical Society, 78 (2): 167—197, doi:10.1017/S1446788700008016, MR 2141875.
- ↑ Погорєлов, О. В. (1949), Квазигеодезические линии на выпуклой поверхности, Математический сборник[en], N.S., 25(67): 275—306, MR 0031767.