Функція Гаусса

У математиці функцією Гаусса (на ім‘я Карла Фрідріха Гаусса) є функція, що виражається залежністю

f(x)=ae^{-{(x-b)^{2} \over 2c^{2}}}

для дійсних чисел константа a > 0, b, c > 0, і e ≈ 2,718281828 (число Ейлера).

Графік функції Гаусса є характерною симетричною кривою у формі дзвону, що швидко спадає на нескінченності. Параметр a є висотою піку кривої, b є позицією центру, і c контролює ширину «дзвону».

Функцію Гаусса широко вживають в:

Статистиці, де вона описує нормальний розподіл;
Обробці сигналу, де нею розраховують фільтри Гаусса, в обробці зображень, де двовимірний гаусіан використовується для гаусового розмивання;
Фізиці, де функцію вживано для розв'язку рівняння теплопровідності і рівняння дифузії;
Математиці, щоб означити перетворення Вейєрштрасса^[en].

Властивості

Гауссова функція виникає, коли діють експоненційною функцією на квадратичну функцію. Гауссова функція є такою, що її логарифм дає квадратичну функцію.

Через параметр c можна виразити ширину піку (FWHM) на половині його висоти згідно з формулою: $\mathrm {FWHM} =2{\sqrt {2\ln 2}}\ c=2,35482...\cdot c.$

Гауссова функція є аналітичною, і її границя при x → ±∞ є 0.

Визначений інтеграл від гауссової функції дає функцію помилок

\operatorname {erf} (x)={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{2}}dt.

Визначений інтеграл з нескінченними границями має властивість

\int _{-\infty }^{\infty }e^{-x^{2}}\,dx={\sqrt {\pi }}

Цей інтеграл рівний 1 тоді і тільки тоді, коли a = 1/(c√(2π)), і в цьому випадку гаусіан є щільністю нормального розподілу випадкової величини з математичним очікуванням μ = b і дисперсією σ² = c².

При перетворенні Фур'є функції Гаусса з параметрами a, b = 0 і c отримуємо іншу функцію Гаусса, з параметрами ac, b = 0 і 1/c. Отже, як частковий випадок, функція Гаусса з b = 0 і c = 1 є інваріантом щодо перетворення Фур'є (вони є власними функціями перетворення Фур'є з власним значенням 1).

Згортка двох гаусіанів є також гаусіаном, із відхиленням c, що рівне середньому квадратичному відхилень тих двох гаусіанів, $c={\sqrt {c_{1}^{2}+c_{2}^{2}}}$ .

Двовимірна функція Гаусса

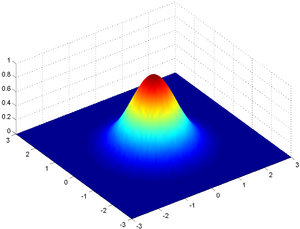
Частковим прикладом формули двовимірної функції Гаусса є

f(x,y)=Ae^{-\left({\frac {(x-x_{o})^{2}}{2\sigma _{x}^{2}}}+{\frac {(y-y_{o})^{2}}{2\sigma _{y}^{2}}}\right)}.

Тут коефіцієнт A називається амплітудою, x_o,y_o визначає центр і σ_x, σ_y визначають «силу розмиття» в напрямку x і y. Фігура ліворуч утворена при A = 1, x_o = 0, y_o = 0, σ_x = σ_y = 1.