Ціла частина числа

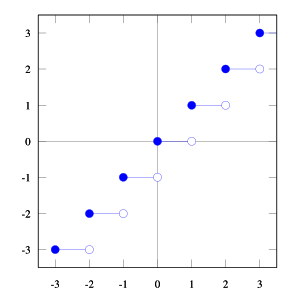
Графік функції $y=[x]$ або $y=\lfloor x\rfloor$

Ціла частина дійсного числа $x$ — найбільше ціле число, яке не більше ніж $x$. Ціла частина числа $x$ зазвичай позначається як $[x]$.

Графік функції $y=\lceil x\rceil$

В інформатиці поряд з функцією ціла частина використовують функції підлога (англ. floor) та стеля (англ. ceiling). Функція підлога позначається як $y=\lfloor x\rfloor$ та збігається з цілою частиною, функція стелі позначається як $\lceil x\rceil$ та дорівнює найменшому цілому числу, яке не менше за $x$.

Визначення за допомогою нерівностей такі:

$\lfloor x\rfloor =\max \,\{m\in \mathbb {Z} \mid m\leqslant x\},$

$\lceil x\rceil =\min \,\{n\in \mathbb {Z} \mid n\geqslant x\}.$

Оскільки в напіввідкритому інтервалі довжини 1 є рівно одне ціле число, то для будь-якого дійсного x існують єдині цілі числа m і n, що задовольняють нерівність

$x-1<m\leq x\leq n<x+1.$

Тоді   $\lfloor x\rfloor =m$   і   $\lceil x\rceil =n$  також можна приймати як означення функцій підлоги та стелі.

Еквівалентності

Наступні формули можна використовувати для спрощення виразів, що включають функцій підлоги та стелі.

${\begin{aligned}\lfloor x\rfloor =m&\;\;{\mbox{ тоді і тільки тоді }}&m&\leq x<m+1,\\\lceil x\rceil =n&\;\;{\mbox{ тоді і тільки тоді }}&n-1&<x\leq n,\\\lfloor x\rfloor =m&\;\;{\mbox{ тоді і тільки тоді }}&x-1&<m\leq x,\\\lceil x\rceil =n&\;\;{\mbox{ тоді і тільки тоді }}&x&\leq n<x+1.\end{aligned}}$

На мові відношень порядку функція підлоги є залишковим відображенням, тобто частиною відповідності Галуа: це верхнє спряження функції, яке вкладує цілі числа в дійсні числа.

${\begin{aligned}x<n&\;\;{\mbox{ тоді і тільки тоді }}&\lfloor x\rfloor &<n,\\n<x&\;\;{\mbox{ тоді і тільки тоді }}&n&<\lceil x\rceil ,\\x\leq n&\;\;{\mbox{ тоді і тільки тоді }}&\lceil x\rceil &\leq n,\\n\leq x&\;\;{\mbox{ тоді і тільки тоді }}&n&\leq \lfloor x\rfloor .\end{aligned}}$

Наступні формули показують, як додавання цілих чисел до аргументу впливає на функції:

${\begin{aligned}\lfloor x+n\rfloor &=\lfloor x\rfloor +n,\\\lceil x+n\rceil &=\lceil x\rceil +n,\\\{x+n\}&=\{x\}.\end{aligned}}$

Вищезазначені формули невірні, якщо n не є цілим числом; однак для будь-яких x, y мають місце наступні нерівності:

${\begin{aligned}\lfloor x\rfloor +\lfloor y\rfloor &\leq \lfloor x+y\rfloor \leq \lfloor x\rfloor +\lfloor y\rfloor +1,\\\lceil x\rceil +\lceil y\rceil -1&\leq \lceil x+y\rceil \leq \lceil x\rceil +\lceil y\rceil .\end{aligned}}$

Співвідношення між функціями

З означень випливає, що

$\lfloor x\rfloor \leq \lceil x\rceil ,$   причому рівність можлива, тоді і тільки тоді, коли x - ціле число, тобто

$\lceil x\rceil -\lfloor x\rfloor ={\begin{cases}0,&{\mbox{якщо}}x\in \mathbb {Z} ,\\1,&{\mbox{якщо}}x\not \in \mathbb {Z} .\end{cases}}$

Насправді для цілих чисел n і значення функцій підлоги і стелі збігаються :

$\lfloor n\rfloor =\lceil n\rceil =n.$

Зміна знаку аргументу, міняє місцями функції підлоги та стелі і змінює знак:

${\begin{aligned}\lfloor x\rfloor +\lceil -x\rceil =0,\\-\lfloor x\rfloor =\lceil -x\rceil ,\\-\lceil x\rceil =\lfloor -x\rfloor ,\end{aligned}}$

і:

$\lfloor x\rfloor +\lfloor -x\rfloor ={\begin{cases}0&{\text{якщо }}x\in \mathbb {Z} \\-1&{\text{якщо }}x\not \in \mathbb {Z} ,\end{cases}}$

$\lceil x\rceil +\lceil -x\rceil ={\begin{cases}0&{\text{ якщо }}x\in \mathbb {Z} \\1&{\text{якщо }}x\not \in \mathbb {Z} .\end{cases}}$

Зміна знаку аргументу доповнює дробову частину:

$\{x\}+\{-x\}={\begin{cases}0,&{\text{якщо}}x\in \mathbb {Z} ,\\1,&{\text{якщо}}x\not \in \mathbb {Z} .\end{cases}}$

Функції підлоги, стелі та дробової частини є ідемпотентними:

${\begin{aligned}{\Big \lfloor }\lfloor x\rfloor {\Big \rfloor }&=\lfloor x\rfloor ,\\{\Big \lceil }\lceil x\rceil {\Big \rceil }&=\lceil x\rceil ,\\{\Big \{}\{x\}{\Big \}}&=\{x\}.\end{aligned}}$

Результатом композиції функцій підлоги та стелі є внутрішня функція:

${\begin{aligned}{\Big \lfloor }\lceil x\rceil {\Big \rfloor }&=\lceil x\rceil ,\\{\Big \lceil }\lfloor x\rfloor {\Big \rceil }&=\lfloor x\rfloor \end{aligned}}$

завдяки властивості тотожності для цілих чисел.

Частки

Якщо m і n цілі числа, а n ≠ 0, то

$0\leq \left\{{\frac {m}{n}}\right\}\leq 1-{\frac {1}{|n|}}.$

Якщо n - натуральне число, то

$\left\lfloor {\frac {x+m}{n}}\right\rfloor =\left\lfloor {\frac {\lfloor x\rfloor +m}{n}}\right\rfloor ,$

$\left\lceil {\frac {x+m}{n}}\right\rceil =\left\lceil {\frac {\lceil x\rceil +m}{n}}\right\rceil .$

Якщо m додатне, то

$n=\left\lceil {\frac {n}{m}}\right\rceil +\left\lceil {\frac {n-1}{m}}\right\rceil +\dots +\left\lceil {\frac {n-m+1}{m}}\right\rceil ,$

$n=\left\lfloor {\frac {n}{m}}\right\rfloor +\left\lfloor {\frac {n+1}{m}}\right\rfloor +\dots +\left\lfloor {\frac {n+m-1}{m}}\right\rfloor .$

Для m = 2 отримуємо

$n=\left\lfloor {\frac {n}{2}}\right\rfloor +\left\lceil {\frac {n}{2}}\right\rceil .$

У загальному випадку, для додатнього m (див.тотожність Ерміта)

$\lfloor mx\rceil =\lceil x\rceil +\left\lceil x-{\frac {1}{m}}\right\rceil +\dots +\left\lceil x-{\frac {m-1}{m}}\right\rceil ,$

$\lfloor mx\rfloor =\lfloor x\rfloor +\left\lfloor x+{\frac {1}{m}}\right\rfloor +\dots +\left\lfloor x+{\frac {m-1}{m}}\right\rfloor .$

Для перетворення між функціями підлоги та стелі можна використати наступні формули (m додатне)

$\left\lceil {\frac {n}{m}}\right\rceil =\left\lfloor {\frac {n+m-1}{m}}\right\rfloor =\left\lfloor {\frac {n-1}{m}}\right\rfloor +1,$

$\left\lfloor {\frac {n}{m}}\right\rfloor =\left\lceil {\frac {n-m+1}{m}}\right\rceil =\left\lceil {\frac {n+1}{m}}\right\rceil -1.$

Для всіх натуральних чисел m і n:

$\sum _{k=1}^{n-1}\left\lfloor {\frac {km}{n}}\right\rfloor ={\frac {\left(m-1\right)\left(n-1\right)+\gcd \left(m,n\right)-1}{2}},$

яка при додатних [[Взаємно прості числа|взаємнопростих} m і n зводиться до

$\sum _{k=1}^{n-1}\left\lfloor {\frac {km}{n}}\right\rfloor ={\frac {1}{2}}\left(m-1\right)\left(n-1\right).$

Оскільки права частина у загального випадку симетрична відносно m і n, то

$\left\lfloor {\frac {m}{n}}\right\rfloor +\left\lfloor {\frac {2m}{n}}\right\rfloor +\dots +\left\lfloor {\frac {\left(n-1\right)m}{n}}\right\rfloor =\left\lfloor {\frac {n}{m}}\right\rfloor +\left\lfloor {\frac {2n}{m}}\right\rfloor +\dots +\left\lfloor {\frac {\left(m-1\right)n}{m}}\right\rfloor .$

І нарешті, для додатних m і n,

${\begin{aligned}&\left\lfloor {\frac {x}{n}}\right\rfloor +\left\lfloor {\frac {m+x}{n}}\right\rfloor +\left\lfloor {\frac {2m+x}{n}}\right\rfloor +\dots +\left\lfloor {\frac {(n-1)m+x}{n}}\right\rfloor \\=&\left\lfloor {\frac {x}{m}}\right\rfloor +\left\lfloor {\frac {n+x}{m}}\right\rfloor +\left\lfloor {\frac {2n+x}{m}}\right\rfloor +\cdots +\left\lfloor {\frac {(m-1)n+x}{m}}\right\rfloor .\end{aligned}}$

це співвідношення іноді називають законом взаємності.

Вкладені частки

Для додатного цілого n і довільних дійсних чисел m, x:

$\left\lfloor {\frac {\lfloor x/m\rfloor }{n}}\right\rfloor =\left\lfloor {\frac {x}{mn}}\right\rfloor ,$

$\left\lceil {\frac {\lceil x/m\rceil }{n}}\right\rceil =\left\lceil {\frac {x}{mn}}\right\rceil .$

Неперервність та розкладення у ряди

Жодна з функцій, обговорюваних у цій статті, не є неперервною, але всі - кусково-лінійні: функції $\lfloor x\rfloor$, $\lceil x\rceil$, і $\{x\}$ мають розриви в цілих числах. Функція $\lfloor x\rfloor$ є напівнеперервною зверху і функції $\lceil x\rceil$ і $\{x\}$ - напівнеперервні знизу.

Оскільки жодна з функцій, розглянутих у цій статті, не є неперервною, тому жодна з них не допускає розклад у вигляді степеневих рядів. Оскільки функції підлоги і стелі неперіодичні, то вони не допускають рівномірно збіжних розкладів у вигляді рядів Фур'є. Функція дробової частини має розклад у ряд Фур'є

$\{x\}={\frac {1}{2}}-{\frac {1}{\pi }}\sum _{k=1}^{\infty }{\frac {\sin \left(2\pi kx\right)}{k}}$

для x не цілого числа.

У точках розриву ряд Фур'є збігається до значення, яке є середнім його границь зліва та справа, на відміну від функцій підлоги, стелі та дробової частини: для фіксованого y і x кратного y ряд Фур'є дає збіжність до y/2, а не до $x\mod y=0$. У точках неперервності ряд збігається до відповідного значення функції.

З формули $\lfloor x\rfloor =x-\{x\}$ отримуємо

$\lfloor x\rfloor =x-{\frac {1}{2}}+{\frac {1}{\pi }}\sum _{k=1}^{\infty }{\frac {\sin(2\pi kx)}{k}}$

для x не цілого числа.

Позначення та приклади

Для цілої частини числа $x$ довгий час використовувалось позначення $[x]$, введене Гаусом.

В 1962 році Кеннет Айверсон запропонував заокруглення числа $x$ до найближчого цілого в меншу і більшу сторони називати «підлога» і «стеля» $x$ і позначати $\lfloor x\rfloor$ і $\lceil x\rceil$ відповідно. У цих позначеннях $[x]=\lfloor x\rfloor$.

В сучасній математиці вживають обидва позначення, $[x]$ і $\lfloor x\rfloor$, однак існує тенденція переходу до термінології і позначень Айверсона. Одна з причин цього — потенційна неоднозначність поняття «ціла частина числа». Наприклад, ціла частина числа 2,7 рівна 2, але можливі дві думки на те, як визначити цілу частину числа −2,7. Відповідно до даного в цій статті визначення $[x]\equiv \lfloor x\rfloor =-3$, однак в деяких калькуляторах наявна функція цілої частини числа INT, для від'ємних чисел визначена як INT(-x) = -INT(x), таким чином INT(-2,7) = −2. В термінології Айверсона відсутні можливі неоднозначності:

${\begin{matrix}\lfloor 2{,}7\rfloor =2,&\lfloor -2{,}7\rfloor =-3,\\\lceil 2{,}7\rceil =3,&\lceil -2{,}7\rceil =-2\end{matrix}}$

Див. також

• Дробова частина числа