Ядро (статистика)

Ядро або ядрова функція — це вагова функція, що використовується в непараметричних методах оцінки. Ядра використовуються при ядерній оцінці щільності розподілу для оцінки густини випадкової величини, чи в ядерній регресії для оцінки умовного математичного сподівання випадкової величини. Ядра також використовуються в часових рядах як переіодограми для оцінки спектральної щільності. Додаткового використання ядра набули в оцінці інтенсивності точкового процесу зміної в часі.

Визначення

Ядром називається невід'ємна дійснозначна інтегровна функція K, яка задовольняє дві наступні властивості:

$\int _{-\infty }^{+\infty }K(u)\,du=1\,;$
$K(-u)=K(u)\ \forall \ u\,.$

Перша умова гарантує, що метод ядерної оцінки щільності розподілу дійсно дає густину випадкової величини. Друга — гарантує, що середнє значення знайденого розподілу дорівнює середньому значенню вибірки для якої оцінюють густину.

Якщо K — ядро, тоді функція K* визначена таким чином K*(u) = λ⁻¹K(λ⁻¹u), де λ > 0 також є ядерною функцією. Цю властивість можна використати для вибору масштабу максимально узгодженого з даними.

Використання ядер

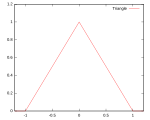
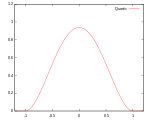
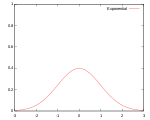
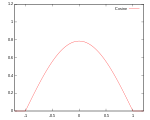
Звичайно використовують кілька видів ядрових функцій: рівномірну, трикутну, Епанечнікова, Четвертинну (двоточкову), кубічну (триточкову), Гауса та косинусну.

В таблиці нижче, 1_{…} — характеристична функція.

Ядрові функції, K(u)		$\textstyle \int u^{2}K(u)du$	$\textstyle \int K^{2}(u)du$
Рівномірна	$K(u)={\frac {1}{2}}\,\mathbf {1} _{\{\|u\|\leq 1\}}$	${\frac {1}{3}}$	${\frac {1}{2}}$
Трикутна	$K(u)=(1-\|u\|)\,\mathbf {1} _{\{\|u\|\leq 1\}}$	${\frac {1}{6}}$	${\frac {2}{3}}$
Епанечнікова	$K(u)={\frac {3}{4}}(1-u^{2})\,\mathbf {1} _{\{\|u\|\leq 1\}}$	${\frac {1}{5}}$	${\frac {3}{5}}$
Четвертинна (двоточкова)	$K(u)={\frac {15}{16}}(1-u^{2})^{2}\,\mathbf {1} _{\{\|u\|\leq 1\}}$	${\frac {1}{7}}$	${\frac {5}{7}}$
Кубічна (триточкова)	$K(u)={\frac {35}{32}}(1-u^{2})^{3}\,\mathbf {1} _{\{\|u\|\leq 1\}}$	${\frac {1}{9}}$	${\frac {350}{429}}$
Гауса	$K(u)={\frac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}u^{2}}$	$1\,$	${\frac {1}{2{\sqrt {\pi }}}}$
Косинус	$K(u)={\frac {\pi }{4}}\cos \left({\frac {\pi }{2}}u\right)\mathbf {1} _{\{\|u\|\leq 1\}}$	$1-{\frac {8}{\pi ^{2}}}$	${\frac {\pi ^{2}}{16}}$
Логістичне	$K(u)={\frac {1}{e^{u}+2+e^{-u}}}$	${\frac {\pi ^{2}}{3}}$	${\frac {1}{6}}$
Сигмоїда	$K(u)={\frac {2}{\pi }}{\frac {1}{e^{u}+e^{-u}}}$	${\frac {\pi ^{2}}{4}}$	${\frac {2}{\pi ^{2}}}$
Ядро Сільвермана^[1]	$K(u)={\frac {1}{2}}e^{-{\frac {\|u\|}{\sqrt {2}}}}\cdot \sin \left({\frac {\|u\|}{\sqrt {2}}}+{\frac {\pi }{4}}\right)$	$0$	${\frac {3{\sqrt {2}}}{16}}$