Тесеракт

Тесеракт
Проєкція 4-вимірного куба на тривимірний простір Натисніть тут, щоб подивитися обертання проєкції
Тип		Правильний 4-політоп
Властивості		Опуклий, рівносторонній,однорідний, вершинно-транзитивний, гране-транзитивний, зонотоп, політоп Ганнера
Комбінаторика
Елементи	8 Комірок	Тривимірні куби {4,3} —
	24 Граней	Квадрати {4} —
	32 Ребер	Відрізки  —
	16 Вершин	Точки (4-го степеня)
Характеристика Ейлера		$\chi =-{\hbox{K}}+\Gamma -{\hbox{P}}+{\hbox{B}}=0$
Вершинна фігура		Правильний тетраедр {3,3} з довжиною сторони ${\sqrt {2}}$
Реберна фігура		Правильний трикутник {3}
Багатокутник Петрі		24 змішаних {8}–{4} -кутників
Класифікація
Символ Шлефлі		$\{4,3,3\}$
		Як кубічна призма: t0,3{4,3,2} або {4,3}×{ } Як 4-4 дуопризма : t0,2{4,2,4} або {4}×{4} t0,2,3{4,2,2} або {4}×{ }×{ } Як 4-кубоїд: t0,1,2,3{2,2,2} або { }×{ }×{ }×{ } ={ }4
Діаграма Коксетера — Динкіна		(або x4o3o3o)
		— як кубічна призма — як 4-4 дуопризма — як 4-кубоїд
Група Коксетера		B4 , [3,3,4]
Двоїстий багатогранник		16-комірник

Тесеракт (від грец. Τέσσερες ἀκτῖνες — «чотири промені») — чотиривимірний гіперкуб — аналог двовимірного квадрата та тривимірного куба в чотиривимірному просторі.

Інші назви:

• 4-Куб (4-Cube);
• 8-комірник (8-cell);
• (правильний) Октохорон (Octachoron) (від грец. οκτώ —"вісім", а грец. χώρος —"місце/простір");
• Тетракуб (Tetracub);
• Гексадекахорон (Hexadecachoron);
• Гіперкуб (про будь-який аналог куба з більш ніж трьома розмірностями);

Багато з цих назв описують його різні особливі властивості.

Згідно з Оксфордським словником, слово «tesseract» було придумано і почало використовуватися в 1888 році Чарльзом Говардом Гінтоном (1853—1907) в його книзі «Нова ера думки» (англ. «A New Era of Thought»), в якій початково він писав це слово як «tessaract».

Тесеракт є одним з шести опуклих правильних політопів 4-вимірного простору .

Подібно до того, як периметр квадрата складається з чотирьох ребер, а поверхня куба — з шести квадратних граней, гіперповерхня тесеракта складається з восьми комірок, що мають форму тривимірного куба і перетинаються під прямим кутом.

При кожному ребрі тесеракта сходиться 3 тривимірних куба

Так само як і тривимірний куб, тессеракт можна розглядати як окремий випадок інших 4-вимірних багатогранників з меншою симетрією. Зокрема, тессеракт є окремим випадком кубічної призми, 4,4-дуопризми та 4-вимірного паралелепіпеда або ортотопа .

4-Куб є мірним політопом чотиривимірного простору і є одиницею виміру гіпероб'єму в ньому, так само, як тривимірний куб з одиничним вимірами є одиницею виміру об'єму тривимірного простору, а одиничний квадрат є одиницею вимірювання площі.

4-Куб є зонотопом, тобто кожна його k-вимірна грань, і він сам володіє центром симетрії. Тесерактами можна замостити 4-вимірний простір без проміжків та накладень.

Двоїстим політопом до 4-куба є 16-комірник, символ Шлефлі якого {3,3,4}

Геометрія

Звичайний тесеракт в Евклідовому чотиривимірному просторі означається як опукла оболонка точок (± 1, ± 1, ± 1, ± 1). Інакше кажучи, він може бути представлений у наступному вигляді:

$[-1,1]^{4}\equiv \{(x_{1},x_{2},x_{3},x_{4})\,:\,-1\leq x_{i}\leq 1\}.$

Тесеракт обмежений вісьмома гіперплощинами $x_{i}=\pm 1,\;i=1,2,3,4$, перетин яких із самим тесерактом задає його тривимірні грані (є звичайними кубами). Кожна пара непаралельних тривимірних граней перетинається, утворюючи двовимірні межі (квадрати), і так далі. Остаточно, тесеракт володіє 8 тривимірними гранями, 24 двовимірними, 32 ребрами і 16 вершинами.

Переріз 4-куба гіперплощиною, паралельною до його 3-D краю є тривимірним кубом. Тобто 4-куб складається з нескінченної множини тривимірних кубів, які є перерізами від його перетину паралельними гіперплощинами між двома протилежними краями.

Аналогічно до того, як в тривимірному кубі перерізом при перетині його площиною, паралельною одній з граней, є плоский квадрат; і таких плоских перерізів між двома паралельними гранями куба є безліч.

Як правильний 4-політоп, тесеракт має символ Шлефлі {4,3,3} з гіпероктаедричною симетрією порядку 384.

Тесеракт можна розглядати як окремий випадок інших 4-вимірних багатогранників з меншою симетрією.

Він є окремим випадком 4- призми, основою якої є тривимірний куб, а бічні сторони також є кубами (кубічна призма). В цьому випадку два паралельні куби, сполучено 6 квадратними призмами (сторонами), тобто політоп є декартовим добутком тривимірної призми та одновимірного відрізку, і має символ Шлефлі {4,3}×{ } та діаграму Коксетера — Динкіна . Має симетрію порядку 96.

Як окремий випадок 4-4 дуопризми , тесеракт є декартовим добутком двох двовимірних квадратів, має символ Шлефлі {4}×{4} та діаграму Коксетера — Динкіна . Має симетрію порядку 64.

Як окремий випадок 4-кубоїда (4-вимірного паралелепіпеда або ортотопа ) тесеракт є декартовим добутком чотирьох одновимірних відрізків, його можна представити символом Шлефлі { }×{ }×{ }×{ } ={ }⁴ та діаграмою Коксетера — Динкіна . Має симетрію порядку 16.

Тесеракт може бути розкладений на менші 4-політопи. Він є опуклою оболонкою сполуки (з'єднання) двох напівтесерактів (16-коміркових). Його також можна розбити на 4-вимірні симплекси (неправильні 5-комірники), які мають спільні вершини з тессерактом. Відомо, що існує 92487256 таких тріангуляцій і що найменша кількість 4-вимірних симплексів у будь-якій з них дорівнює 16.

Оскільки в кожній вершині тесеракта сходяться чотири ребра, його вершинною фігуою є правильний тетраедр.

Кількість способів розфарбувати тессеракт, щоб комірки мали різні кольори дорівнює 8!/192 = 210 : група кольорів є групою перестановок з 8 елементів і має розмір 8!, тоді як порядок чистої обертової симетрії тесеракта дорівнює 192 (половина від повної симетрії, тобто 384 елементів).

Формули

Для 4-вимірного гіперкуба, довжина ребер якого дорівнює a:

		Радіус вписаної гіперсфери (4D) (торкається комірок в їх центрах)	$r_{4}={\frac {1}{2}}\cdot a$
Діагональ між вершинами грані	$d_{2}={\sqrt {2}}\cdot a\approx 1.414213\cdot a$	Радіус напіввписаної сфери (торкається граней в їх центрах)	$R_{2}={\frac {\sqrt {2}}{2}}\cdot a\approx 0.707107\cdot a$
Діагональ між вершинами комірки	$d_{3}={\sqrt {3}}\cdot a\approx 1.732051\cdot a$	Радіус напіввписаної сфери (торкається ребер в їх серединахах)	$R_{3}={\frac {\sqrt {3}}{2}}\cdot a\approx 0.866025\cdot a$
Діагональ політопа (4D) (найдовша діагональ між вершинами, діаметр тесеракта)	$d_{4}={\sqrt {4}}\cdot a=2a$	Радіус описаної гіперсфери (4D) (проходить через всі вершини)	$R_{4}={\frac {\sqrt {4}}{2}}\cdot a=a$
Площа поверхні (2D) (2D площа всіх граней)	$S=24a^{2}$
Гіперплоща поверхні (3D) (3D об'єм всіх комірок)	$V_{3}=8a^{3}$	Двогранний кут між гранями	${\frac {\pi }{2}}$ (радіан)
Гіпероб'єм (4D)	$V_{4}=a^{4}\,$	Кут між комірками	${\frac {\pi }{2}}$ (радіан)

Точка в 4-вимірному просторі

Нехай описана сфера тесеракта має радіус R. Нехай дано довільну точку в 4-вимірному просторі і відстані від неї до вершин 4-куба дорівнюють d_i . Тоді виконується рівність: ^{:стор.229, теор.2}

${\frac {1}{16}}\cdot \sum _{i=1}^{16}d_{i}^{4}+{\frac {5R^{4}}{4}}=\left({\frac {1}{16}}\cdot \sum _{i=1}^{16}d_{i}^{2}+{\frac {R^{2}}{2}}\right)^{2}.$

Декартові координати вершин

Декартові координати 16-ти вершин тесеракта з довжиною ребра $a=1$, центр якого знаходиться в початку координат, мають значення:

• $\left(\pm {\frac {1}{2}},\pm {\frac {1}{2}},\pm {\frac {1}{2}},\pm {\frac {1}{2}}\right)$

При цьому 4-куб буде зорієнтовано паралельно координатним осям.

Популярний опис

Анімація зміщення у вимірах

Побудову гіперкубів можна уявити наступним чином:

• 1-вимірний куб (відрізок): Дві точки A і B можна з'єднати в один відрізок AB довжиною l .

• 2 вершини // 1 ребро

• 2-вимірний куб (квадрат): На двовимірній площині паралельно до відрізка AB на відстані l від нього проведемо відрізок CD і з'єднаємо їх кінці. Утворився квадрат ACDB.

• 4 вершини // 4 ребра // 1 грань

• 3-вимірний куб (куб): В тривимірному просторі розмістимо два паралельні квадрати ABCD і EFGH на відстані l один від одного. З'єднаємо відповідні вершини відрізками і отримаємо тривимірний куб ABCDEFGH.

• 8 вершин // 12 ребер // 6 граней // 1 об'єм (комірка)

• 4-вимірний куб: Зсунувши тривимірний куб в четвертому вимірі (перпендикулярно першим трьом) на відстань l, ми отримаємо гіперкуб CDBAGHFEKLJIOPNM. Однак таке паралельне розміщення двох кубів, при якому 8 відповідних пар вершин розділені відстанню l, може бути досягнуто лише у просторі 4-х або більше вимірів.

• 16 вершин // 32 ребра // 24граней // 8 комірок // 1 4D-об'єм

Модель побудови гіперкуба

Одновимірний відрізок АВ служить стороною двовимірного квадрата CDBA, квадрат — стороною куба CDBAGHFE, який, в свою чергу, буде стороною чотиривимірного гіперкуба. Відрізок прямої має дві граничні точки, квадрат — чотири вершини, куб — вісім. В чотиривимірному гіперкубі, таким чином, виявиться 16 вершин: 8 вершин вихідного куба і 8 зрушеного в четвертому вимірі. Він має 32 ребра — по 12 дають початкове і кінцеве положення вихідного куба, і ще 8 ребер «намалюють» вісім його вершин, що перемістилися в четвертий вимір. Ті ж міркування можна виконати і для граней гіперкуба. У двовимірному просторі вона одна (сам квадрат), у куба їх 6 (по дві грані від переміщення квадрата і ще чотири опишуть його збоку). Чотиривимірний гіперкуб має 24 квадратні грані — 12 квадратів вихідного куба в двох положеннях і 12 квадратів від дванадцяти його ребер.

Як сторонами квадрата є 4 одновимірних відрізки, а сторонами (гранями) куба є 6 двомірних квадратів, так і для «чотиривимірного куба» сторонами є 8 тривимірних кубів.

Аналогічним чином можна продовжити міркування для гіперкубів більшого числа вимірів, але набагато цікавіше подивитися, як для нас, жителів тривимірного простору, буде виглядати чотиривимірний гіперкуб. Скористаємося для цього вже знайомим шляхом аналогій.

Візьмемо дротяний куб ABCDHEFG і подивимося на нього одним оком з боку межі. Ми побачимо і можемо намалювати на площині два квадрата (ближню і дальню його межі), з'єднані чотирма лініями — бічними ребрами. Аналогічним чином чотиривимірний гіперкуб у просторі трьох вимірів буде виглядати як два кубічних «ящики», вставлених один в одного і з'єднаних вісьмома ребрами. При цьому самі «ящики» — тривимірні грані — будуть проєктуватися на «наш» простір, а лінії, які їх з'єднують, простягнуться в напрямку четвертої осі.

Сам же чотиривимірний гіперкуб складається з нескінченної кількості кубів, подібно до того як тривимірний куб можна «нарізати» на нескінченну кількість плоских квадратів.

Розгортка тесеракта

Аналогічно тому, як поверхню куба можна розгорнути у двовимірний багатокутник, що складається з шести квадратів, поверхню тесеракта можна розгорнути у тривимірне тіло, що складається з восьми кубів (октокуб).

Розгортка тесеракта

Анімація розгортання поверхні тесеракта у тривимірний простір

Існує 261 розгортка тесеракта.

Розгортки 4-куба можуть бути знайдені перерахуванням «здвоєних дерев», де «здвоєне дерево» (paired tree) — це дерево з парним числом вершин, які розбиті на пари так, що жодна пара не складається з двох суміжних вершин. Між «здвоєними деревами» з 8 вершинами і розгортками тесеракта існує взаємно однозначна відповідність. Всього існує 23 дерева з 8 вершинами, при розбитті вершин яких на пари несуміжних вершин виходить 261 «здвоєне дерево» з 8 вершинами.

Всі тривимірні розгортки теcеракта замощують тривимірний простір без проміжків та накладень. Тобто кожна з них може утворювати стільник.

Однією з розгорток тесеракта є розгортка, що імітує розгортку тривимірного куба в латинський хрест: вона складена з чотирьох кубів поєднаних квадратними гранями один поверх одного та ще з чотирьох кубів, прикріплених до вільних квадратних граней другого зверху куба; в результаті формується тривимірний подвійний хрест. Сальвадор Далі використовував цю форму в його праці «Розп'яття» (1954). На честь Далі, цей октокуб був названий хрест Далі.

У оповіданні Роберта А. Гайнлайна «І побудував він будинок» каліфорнійський архітектор Квінтус Тіл будує восьмикімнатний дім у формі розгортки гіперкуба, який під час землетрусу складається в чотиривимірний тесеракт.

Граф тесеракта

Граф тесеракта
Позначення графа: Q4
Вершин	16
Ребер	32
Радіус	4
Діаметр	4
Обхват	4
Автоморфізм	384
Хроматичне число	2
Властивості	Регулярний, непланарний, простий, зв'язний, симетричний, Гамільтонів, Ейлерів, граф Келі, циклічний, вершинно-транзитивний, реберно-транзитивний, дистанційно-транзитивний, двочастковий, дистанційно-регулярний

В теорії графів граф тесеракта — це граф з 16 вершинами та 32 ребрами, що має кістяк 4-куба.

Всі 18 вершин графа мають степінь 4, а отже, граф є графом 4-го степеня (англ. quartic).

Цей граф є окремим випадком графа гіперкуба.

Спектр графа : $Spec(G)=(-4)^{1}(-2)^{4}\,0^{6}\,2^{4}\,4^{1}$

Граф є двочастковими — його вершини можна розфарбувати тільки двома кольорами.

Гамільтонові цикли

Граф тесеракта є гамільтоновим та ейлеровим, тобто має гамільтонові та ейлерові цикли. Гамільтонів цикл — замкнений шлях, що проходить через кожну вершину графа рівно один раз. Гамільтонів шлях між вершинами U, V існує тоді і тільки тоді, коли u и v мають різні кольори в двокольоровому розфарбуванні графа.

Інші властивості

Граф гіперкуба Q₄ :

• є діаграмою Хассе кінцевої булевої алгебри;

• є транзитивним щодо дуг та симетричним;

• містить всі цикли довжини 4, 6, 8 і тому є біпанциклічним графом;
• може бути зображений як граф одиничних відстаней на евклідовій площині шляхом вибору одиничного вектора для кожного елемента  множини і розміщення кожної вершини, відповідно множини S, як суму векторів із S;

• є вершинним 4-зв'язним графом за теоремою Балинського;

• власні значення матриці інцидентності рівні (-4, -2, 0, 2, 4), а власні значення матриці Кірхгофа графа рівні (0,2, …, 8);

• Ізопериметричне число дорівнює h(G)=1.
• Граф Q₄ — це граф Леві конфігурації Мебіуса. Він також є графом ходів коня для тороїдальної шахівниці $4\times 4$.

Проєкції

На двовимірний простір

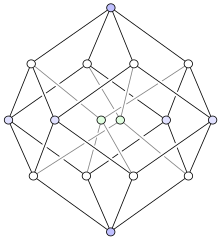
Модель чотиривимірного тесеракта можливо побудувати у двовимірному просторі (на площині) у вигляді графів — вершин та ребер, що з'єднують відповідні вершини, спираючись на модель побудови тесеракта шляхом зсуву тривимірного куба в четвертий вимір. Проєктування на площину дозволяє легко зрозуміти розташування вершин гіперкуба. Таким чином, можна отримати зображення, які більше не відображають просторових відношень у межах тесеракта, але які ілюструють структуру зв'язків вершин, як у попередніх прикладах:

Показує як отримати проєкцію тесеракта шляхом поєднання двох кубів

Ілюструє той факт, що всі ребра тесеракта мають однакову довжину.Проєкція примітна тим, що всі вісім кубів мають однаковий вигляд.

Демонструє тесеракт в ізометрії відносно точки побудови. Це зображення потрібне при використанні тесеракта як підстави для топологічної мережі, щоб зв'язати багаторазові процесори в паралельних обчисленнях.

На тривимірний простір

3D-проєкція тесеракта, що виконує просте обертання навколо площини в 4-вимірному просторі.

3D-проєкція тесеракта, що здійснює подвійне обертання навколо двох ортогональних площин у 4-вимірному просторі.

Перспектива з усуненням прихованого об'єму. Червоний кут є найближчим у 4D і має 4 кубічні комірки, що сходяться навколо нього.

Одна з проєкцій тесеракта на тривимірний простір являє собою два вкладених тривимірних куба, відповідні вершини яких з'єднані між собою відрізками. Внутрішній і зовнішній куб мають різні розміри в тривимірному просторі, але в чотиривимірному просторі це рівні куби. Для розуміння рівності всіх кубів тесеракта була створена модель тесеракта що обертається.

Шість « зрізаних пірамід », які видно по краях на зображеннях проєкції тесеракта — це зображення рівних шести кубів. Однак ці куби для тесеракта — як квадрати (межі) для куба.

Ще одна цікава проєкція тесеракта на тривимірний простір має вигляд ромбододекаедра з проведеними чотирма його діагоналями, що з'єднують пари протилежних вершин при великих кутах ромбів. При цьому 14 з 16 вершин тесеракта проєктуються в 14 вершин ромбододекаедра, а проєкції інших 2, що залишилися, збігаються в його центрі. У такій проєкції на тривимірний простір зберігаються рівність і паралельність всіх одновимірних, двовимірних і тривимірних сторін.

Отрогональні проєкції тесеракта на тривимірний простір

Оболонки паралельних проєкцій тесеракта (різні кольори граней відповідають різним спроєктованим коміркам)

Опукла оболонка проєкції, центрованій по вершині тесеракта формує ромбододекаедр. Кількість вершин у шарах цієї проекції — 1 4 6 4 1 — четвертий ряд у трикутнику Паскаля.

Паралельна проєкція, центрована по комірці тесеракта (англ. The cell-first parallel projection) на тривимірний простір має оболонку у формі тривимірного куба. Найближча та найвіддаленіша комірки проєктуються на куб, а решта шість комірок проектуються на шість квадратних граней куба.

Паралельна проєкція, центрована по грані тесеракта (англ. The face-first parallel projection) на тривимірний простір має кубоїдну оболонку у формі прямокутного паралелепіпеда. Дві пари комірок проєктуються на верхню і нижню половини цієї оболонки, а чотири інші — на бічні грані.

Паралельна проєкція, центрована по ребру тесеракта (англ. The edge-first parallel projection) на тривимірний простір має оболонку у вигляді шестикутної призми. Шість комірок проєктуються на ромбічні призми, які вкладено в шестикутну призму аналогічно до того, як грані 3D-куба проєктуються на шість ромбів у шестикутній оболонці при проєкції, центрованій по вершині. Дві інші комірки проєктуються на основи призми.

Паралельна проєкція, центрована по вершині тесеракта (англ. The vertex-first parallel projection) на тривимірний простір має оболонку у вигляді ромбододекаедра. Дві вершини тесеракта проєктуються на початок координат. Існує рівно два способи розбиття ромбододекаедра на чотири конгруентних ромбоедра, що дають загалом вісім можливих ромбоедрів, кожен з яких є спроектованим кубом тессеракта. Ця проекція також має максимальний об'єм. Один набір векторів проекцій: u = (1,1,-1,-1), v = (-1,1,-1,1), w = (1,-1,-1,1).

Ортографічні проєкції тесеракта

Площина Коксетера	B4	B4 --> A3	A3
Граф
Діедрична симетрія	[8]	[4]	[4]
Площина Коксетера	Інше	B3 / D4 / A2	B2 / D3
Граф
Діедрична симетрія	[2]	[6]	[4]

Анімація, що показує кожен окремий куб у проекції тесеракта на площину Коксетера B4	Ортографічна проєкція графа на площину Коксетера B4 (штриховими лініями показано приховані дальні ребра), і проєкція тесеракта без прихованих ліній.

Стереопроєкції

Стереозображення або стереопара тесеракта зображується як дві проєкції на площину одного з варіантів тривимірного представлення тесеракта. Стереопара розглядається так, щоб кожне око бачило тільки одне з цих зображень, виникає стереоскопічний ефект, що дозволяє краще сприйняти проєкцію тесеракта на тривимірний простір.

Стереозображення ортогональної проєкції тесеракту	Стереоскопічна 3D проєкція тесеракту (паралельний вид)	Стереоскопічна 3D проєкція розгорнутого тесеракту

Стереографічна проєкція тесеракта (Ребра проєктуються на 3-сферу)

Пов'язані та споріднені 4-політопи

Тесеракт є четвертим в нескінченній родині n-вимірних гіперкубів:

Ортографічні проєкції n-вимірних гіперкубів

Лінійний відрізок	Квадрат	Куб	4-куб Тесеракт	5-куб, Пентеракт	6-куб Гексеракт	7-куб Гептеракт	8-куб Октеракт	9-куб Ентенеракт	10-куб Декеракт
Символ Шлефлі	$\{4\}$	$\{4,3\}$	$\{4,3,3\}$	$\{4,3,3,3\}$	$\{4,3,3,3,3\}$	$\{4,\underbrace {3,\cdots 3} _{5}\}$	$\{4,\underbrace {3,\cdots 3} _{6}\}$	$\{4,\underbrace {3,\cdots 3} _{7}\}$	$\{4,\underbrace {3,\cdots 3} _{8}\}$

Тесеракт (8-комірник) є одним з шести опуклих правильних 4-політопів.

Опуклі правильні 4-політопи
Група симетрії	A4	B4		F4	H4
Назва	5-комірник 4-гіпертетраедр	16-комірник 4-гіпероктаедр	8-комірник 4-гіперкуб	24-комірник	600-комірник 4-піперікосаедр	120-комірник 4-піпердодекаедр
Символ Шлефлі	{3, 3, 3}	{3, 3, 4}	{4, 3, 3}	{3, 4, 3}	{3, 3, 5}	{5, 3, 3}
Діаграма Коксетера — Динкіна
Граф
Вершини	5 (вершинна фігура — тетраедр)	8 (в. ф. — октаедр)	16 (в. ф.— тетраедр)	24 (в. ф. — куб)	120 (в. ф. — ікосаедр)	600 (в. ф. — тетраедр)
Ребра	10 (реберна фігура — прав. трикутник)	24 (р. ф. — квадрат)	32 (р. ф. — прав. трикутник)	96 (р. ф. — прав. трикутник)	720 (р. ф. — прав. п'ятикутник)	1200 (р. ф. — прав. трикутник)
Грані	10 правильних трикутників	32 правильних трикутників	24 квадратів	96 правильних трикутників	1200 правильних трикутників	720 правильних п'ятикутників
Комірки	5 правильних тетраедрів	16 правильних тетраедрів	8 кубів	24 правильних октаедрів	600 правильних тетраедрів	120 правильних додекаедрів
Скільки можна вписати в n- комірник	120 в 120-комірник	675 в 120-комірник	2 в 16-комірник	3 в 8-комірник	25 в 24-комірник	10 в 600-комірник
Радіус описаної гіперсфери $R_{4}$	$1$	$1$	$1$	$1$	$1$	$1$
Довжина ребра	${\sqrt {\tfrac {5}{2}}}\approx 1.581$	${\sqrt {2}}\approx 1.414$	$1$	$1$	${\tfrac {1}{\varphi }}\approx 0.618$	${\tfrac {1}{\varphi ^{2}{\sqrt {2}}}}\approx 0.270$
Радіус вписаної гіперсфери $r_{4}$	${\tfrac {1}{4}}$	${\tfrac {1}{2}}$	${\tfrac {1}{2}}$	${\sqrt {\tfrac {1}{2}}}\approx 0.707$	${\sqrt {\tfrac {\varphi ^{4}}{8}}}\approx 0.926$	${\sqrt {\tfrac {\varphi ^{4}}{8}}}\approx 0.926$
Площа поверхні $S$ (2D) (2D площа всіх граней)	$10\cdot {\tfrac {5{\sqrt {3}}}{8}}\approx 10.825$	$32\cdot {\sqrt {\tfrac {3}{4}}}\approx 27.713$	$24$	$96\cdot {\sqrt {\tfrac {3}{16}}}\approx 41.569$	$1200\cdot {\tfrac {\sqrt {3}}{4\varphi ^{2}}}\approx 198.48$	$720\cdot {\tfrac {\sqrt {25+10{\sqrt {5}}}}{8\varphi ^{4}}}\approx 90.366$
Гіперплоща поверхні $V_{3}$ (3D) (3D об'єм всіх комірок)	$5\cdot {\tfrac {5{\sqrt {5}}}{24}}\approx 2.329$	$16\cdot {\tfrac {1}{3}}\approx 5.333$	$8$	$24\cdot {\tfrac {\sqrt {2}}{3}}\approx 11.314$	$600\cdot {\tfrac {\sqrt {2}}{12\varphi ^{3}}}\approx 16.693$	$120\cdot {\tfrac {15+7{\sqrt {5}}}{4\varphi ^{6}{\sqrt {8}}}}\approx 18.118$
Гіпероб'єм $V_{4}$ (4D)	${\tfrac {\sqrt {5}}{24}}\left({\tfrac {\sqrt {5}}{2}}\right)^{4}\approx 0.146$	${\tfrac {2}{3}}\approx 0.667$	$1$	$2$	${\tfrac {r_{4}\times V_{3}}{4}}\approx 3.863$	${\tfrac {r_{4}\times V_{3}}{4}}\approx 4.193$

Тесеракт у культурі

• Тесеракт є предметом кількох науково-фантастичних творів. Зокрема, у фантастичному оповіданні Роберта А. Гайнлайна «І побудував він будинок» (1941 року) каліфорнійський архітектор Квінтус Тіл будує восьмикімнатний дім у формі розгортки гіперкуба, який під час землетрусу складається в чотиривимірний тесеракт.
• Іспанський художник Сальвадор Далі зобразив розгортку тесеракта на своїй картині Розп'яття або Гіперкубічне тіло (1954 рік).
• TesseracT — назва британського гурту, що грає у стилі прогресивного металу.
• З'являється у фільмі Крістофера Нолана «Інтерстеллар» як частина «кротовини» (місту Розена-Ейштейна).
• У фантастично-науковому фільмі режисера Анджея Секули «Куб 2. Гіперкуб» (2002 року) група людей, долаючи перешкоди, мусить вибратися з приміщення-пастки, що знаходиться всередині 4-вимірного тесеракта, до того, як гіперкуб складеться в точку. У цьому гіперкубі створюються і перетинаються паралельні світи, час у деяких кімнатах тече не лінійно.

Див. також

• 4-політоп
• Гіперкуб
• Пентеракт

Література

• Людина, яка «бачила» четвертий вимір // Гіперпростір / Мічіо Кайку ; Пер. з англійської Анжела Кам’янець / Наук. ред. Іван Вакарчук. — Львів : Літопис, 2019. — С. 75-100.
• Harold S. M. Coxeter. Regular Polytopes. — 3rd. — New York : Dover, 1973. — ISBN 0-486-61480-8.

• Peter Turney. Unfolding the Tesseract // Journal of Recreational Mathematics. — 1984-85. — Т. 17, № 1. — С. 1-20. Архівовано з джерела 25 липня 2018.

• Charles H. Hinton. Fourth Dimension, 1904. ISBN 0-405-07953-2
• Ian Stewart, Concepts of Modern Mathematics, 1995. ISBN 0-486-28424-7

Посилання

• Weisstein, Eric W. Tesseract(англ.) на сайті Wolfram MathWorld.
• Tesseract(англ.) на сайті Polytope Wiki.
• Klitzing, Richard. "tes".
• Quickfur. "The Tesseract"
• Hi.gher.Space Wiki Contributors. "Geochoron"