Восьмиточковий алгоритм
Ця стаття не містить посилань на джерела. (квітень 2021) |
Восьмиточковий алгоритм — це алгоритм, який використовується в комп'ютерному баченні для оцінки істотної матриці або фундаментальної матриці, що відповідає парі камер, за допомогою множини відповідних точок двох зображень. Х'ю Крістофер Лонгет-Хіггінс[en] запропонував цей алгоритм у випадку істотної матриці у 1981 році. Теоретично цей алгоритм може бути використано і для визначення фундаментальної матриці, але на практиці нормалізований восьмиточковий алгоритм, описаний Річардом Хартлі 1997 року, більше підходить для цього випадку.
Назва алгоритму походить від того факту, що він оцінює істотну матрицю або фундаментальну матрицю по множині з восьми (або більше) відповідних точок зображення. Однак варіації алгоритму можуть бути використані у випадку менш ніж на восьми точок.
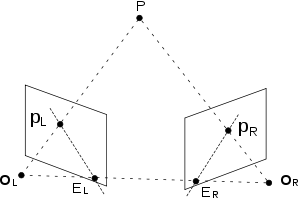
Можна виразити епіполярну геометрію двох камер та точки простору за допомогою алгебраїчного рівняння. Зверніть увагу, незалежно від того де знаходиться точка у просторі, вектори , і належать одній площині. Позначимо як координати точки у системі координат лівого ока та як координати точки у системі координат правого ока; позначимо як обертання та переміщення при переході між системами координат, тобто - це співвідношення між координатами у двох системах координат. Наступне рівняння завжди виконується, оскільки вектор, отриманий як є ортогональним до обох векторів і :
Оскільки матриця обертання є ортогональною, тобто , ми отримуємо
- .
Замінивши на , ми отримуємо
Зверніть увагу на те, що векторний добуток може розглядатися як множення вектора на матрицю; Символом було позначено цю матрицю. Добуток часто називають істотною матрицею і позначають .
Вектори паралельні векторам і тому обмеження копланарності виконується, якщо ми підставляємо ці вектори. Якщо ми позначимо як координати проєкцій на площини лівого та правого зображення, тоді умова копланарності може бути записана як
Далі описано базовий восьмиточковий алгоритм для оцінки істотної матриці . Він складається з трьох кроків. Спочатку формулюється однорідне лінійне рівняння, де розв'язком є матриця , а потім розв’язується це рівняння, враховуючи, що воно може не мати точного розвʼязку. Нарешті, накладаються внутрішні обмеження результуючої матриці. Перший крок описаний у роботі Лонгет-Гіггінса, другий і третій кроки є стандартними підходами в теорії оцінки.
Умова компланарності накладена суттєвою матрицею :
для відповідних точок зображення, представлених у нормалізованих координатах зображення . Задача, яку вирішує алгоритм, полягає у визначенні для набору відповідних точок зображення. На практиці на координати зображення точок зображення впливає шум, і рішення також може бути надмірно визначеним, що означає, що не вдасться знайти яка задовольняє вищезазначеним умовам точно для всіх точок. Це питання розглядається на другому етапі алгоритму.
Крок 1: Формулювання однорідного лінійного рівняння
[ред. | ред. код]Запишемо
- і і
тоді умову компланарності можна переписати як
або
де
- і
це, представляє істотну матрицю у вигляді 9-мірного вектора, і цей вектор повинен бути ортогональним вектору .
Кожна пара відповідних точок зображення створює вектор . Дано набір 3D-точок що відповідає набору векторів , всі вони повинні задовольнити
для вектора . Якщо надано достатньо (принаймні вісім) лінійно незалежних векторів вектор можна визначити вирішивши систему лінійних рівнянь. Запишемо усі вектори як стовпці матриці і тоді:
Це означає що є рішенням системи лінійних однорідних рівнянь.
Стандартний підхід до вирішення цього рівняння передбачає, що є лівим сингулярним вектором якому відповідає нульове сингулярне значення. За умови, що принаймні вісім лінійно незалежних векторів використовуються для побудови випливає, що цей особливий вектор є унікальним і, отже, і можна визначити.
У випадку, коли для побудови використовується більше восьми відповідних точок не виключено, що вона не має жодного особливого значення, рівного нулю. Цей випадок трапляється на практиці, коли на координати зображення впливають різні типи шумів. Поширеним підходом до вирішення цієї задачі є використання методу найменших квадратів; знаходиться що мінімізує
коли . Роз'язок полягає у виборі як лівого сингулярного вектора, що відповідає найменшому особливому значенню . Переписавши цей вектор знову як матрицю отримаємо результат цього кроку, що далі позначено як
Іншим наслідком роботи з шумними координатами зображень є те, що отримана матриця може не задовольняти внутрішнім обмеженням істотної матриці, тобто два її особливих значення є рівними і ненульовими, а інше дорівнює нулю. Залежно від імплементації, менші або більші відхилення від внутрішніх обмежень можуть бути, а можуть і не бути проблемою. Якщо критично важливо, щоб знайдена матриця задовольняла внутрішнім обмеженням, це може бути досягнуто шляхом пошуку матриці рангу 2, яка мінімізує
де є матрицею отриманою на кроці 2 та використовується норма матриці Фробеніуса . Рохзвʼязок задається обчисленням сингулярного розкладу значення :
де є ортогональними матрицями та є діагональною матрицею, яка містить особливі значення . В ідеальному випадку один з діагональних елементів має бути нульовим або принаймні малим порівняно з двома іншими, які повинні бути однаковими. У будь-якому випадку вважаємо
де - найбільше та друге за величиною сингулярні значення відповідно. Нарешті,
Матриця є результуючою оцінкою істотної матриці, отриманою за допомогою алгорита.
Восьмиточковий алгоритм реалізовано в бібліотеці OpenCV, де йому відповідає функція cv::findFundamentalMat [Архівовано 4 березня 2021 у Wayback Machine.], яка викликається із параметром cv::FM_8POINT.
- Richard I. Hartley (June 1997). In Defense of the Eight-Point Algorithm. IEEE Transactions on Pattern Recognition and Machine Intelligence. 19 (6): 580—593. doi:10.1109/34.601246.
- Richard Hartley and Andrew Zisserman (2003). Multiple View Geometry in computer vision. Cambridge University Press. ISBN 978-0-521-54051-3.
- H. Christopher Longuet-Higgins (September 1981). A computer algorithm for reconstructing a scene from two projections. Nature. 293 (5828): 133—135. doi:10.1038/293133a0.





















































