Сингулярний розклад матриці

Візуалізація SVD двовимірної, дійсної матриці зсуву M. Спершу, ми бачимо блакитний одиничний диск з двома векторами стандартного базису. Потім ми бачимо дію M, яка перетворює диск на еліпс. SVD розкладає M на три простих перетворення: початковий поворот V^*, масштабування Σ уздовж осі координат і кінцевий поворот U. Довжини півосей σ₁ і σ₂ є сингулярними значеннями (квадратами власних значень) M, а саме Σ_1,1 і Σ_2,2.

Візуалізація матричного множення в СПМ

Сингуля́рний ро́зклад ма́триці (сингулярне представлення матриці чи англ. singular-value decomposition, SVD) — один з важливих методів розкладу матриці з дійсними або комплексними числами. Є узагальненням власного розкладу матриці невід'ємно визначеної нормальної матриці (наприклад, симетричної матриці з додатними власними значеннями) на матрицю розміру $m\times n$ як узагальнення полярного розкладу.

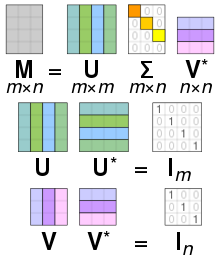
Формально, сингулярний розклад матриці $\mathbf {M}$ розміру $m\times n$, яка складена з дійсних або комплексних чисел, буде розкладанням на множники у вигляді $\mathbf {U\Sigma V^{*}}$, де $\mathbf {U}$ — матриця розміру $m\times m$ буде дійсною або комплексною унітарною матрицею, $\mathbf {\Sigma }$ буде $m\times n$-прямокутною діагональною матрицею з не від'ємними дійсними числами на діагоналі, і $\mathbf {V}$ буде дійсною або комплексною унітарною матрицею розміру $n\times n$. Діагональні елементи $\sigma _{i}$ матриці $\mathbf {\Sigma }$ відомі як сингулярні значення матриці $\mathbf {M}$. Стовпчики $\mathbf {U}$ та стовпчики $\mathbf {V}$ називаються ліво-сингулярними векторами та право-сингулярними векторами матриці $\mathbf {M}$, відповідно.

Сингулярний розклад матриці можна обчислити за допомогою наступних спостережень:

• Ліво-сингулярні вектори M є множиною ортонормованих головних векторів MM^∗.
• Право-сингулярні вектори M є множиною ортонормованих головних векторів M^∗M.
• Не нульові сингулярні значення M (знаходяться на діагоналі Σ) є квадратними коренями не нульових головних значень як M^∗M, так і MM^∗.

Сингулярний розклад матриці застосовується в лінійній алгебрі для обчислення псевдоінверсії, наближення матриці, обчислення ядра або рангу матриці та інше.

Визначення

Якщо M — матриця розміру m×n чиї елементи беруться з поля K, що може бути полем дійсних або комплексних чисел.

Тоді, невід'ємне дійсне число σ є сингулярним числом для M тоді і тільки тоді, коли існують вектори одиничної довжини u ∈ K^m, v ∈ Kⁿ що виконується:

$\left\{{\begin{matrix}Mv=\sigma u\\M^{*}u=\sigma v.\end{matrix}}\right.$

Вектори u та v називаються відповідно сингулярним зліва вектором та сингулярним справа вектором для σ.

Для матриці M існує наступне представлення, що називається сингулярним розкладом матриці:

$M=U\Sigma V^{*},\!$

де

U — унітарна матриця розміру m×m над полем K,

V* — ермітове спряження унітарної матриці матриці V розміру n×n над полем K,

Σ — діагональна матриця розміру m×n з числами σ на діагоналі,

числа σ зазвичай розташовують в спадаючому порядку, тому матриця Σ однозначно визначається матрицею M.

Сингулярні числа, для яких існують два і більше лінійно незалежних сингулярних векторів називаються виродженими.

Невироджені сингулярні числа мають по одному лівому та правому сингулярному вектору з точністю до множника e^iφ (в випадку дійсних чисел з точністю до знака).

Властивості

• Стовпці U та V є сингулярними зліва та сингулярними справа векторами для M відповідно.

• Кількість ненульових чисел на діагоналі матриці Σ рівне rank Σ = rank M = r (ранг), тому можна скоротити матриці U та V до r стовпців, а матрицю Σ до розміру r×r і отримаємо:

$M={\begin{pmatrix}u_{1}\vdots \ldots \vdots \,u_{r}\end{pmatrix}}{\begin{pmatrix}\sigma _{1}&0&0\\0&\ddots &0\\0&0&\sigma _{r}\end{pmatrix}}{\begin{pmatrix}v_{1}^{*}\\\vdots \\v_{r}^{*}\end{pmatrix}}=\sum _{i=1}^{r}\sigma _{i}\,u_{i}\,v_{i}^{*}.$

Зв'язок SVD з власними значеннями матриці

SVD існує для всіх прямокутних матриць, на відміну від власних векторів і розкладу по ньому, що існує тільки для деяких квадратних матриць.

Використавши формулу SVD для M та M^*, отримаємо:

$MM^{*}=U\Sigma V^{*}\,(V\Sigma U^{*})=U\Sigma ^{2}U^{*}$

$M^{*}M=V\Sigma U^{*}\,(U\Sigma V^{*})=V\Sigma ^{2}V^{*}$

Права сторона є розкладом по власних векторах лівої сторони:

• Ненульові елементи Σ² є власними значеннями для матриць $MM^{*}$ та $M^{*}M,$ тому ці матриці є невід'ємноозначеними (частковий випадок ермітових матриць);
• Стовпці матриці U є власними векторами матриці $MM^{*}$;
• Стовпці матриці V є власними векторами матриці $M^{*}M$.

Цей же результат також можна отримати з визначення сингулярних значень і векторів:

$\left\{{\begin{matrix}MM^{*}u=\sigma ^{2}u,\\M^{*}Mv=\sigma ^{2}v.\end{matrix}}\right.$

Псевдоінверсія

Якщо матрицю можна розкласти як $M=U\Sigma V^{*}$, то її псевдообернена матриця буде дорівнювати

$\ M^{+}=V\Sigma ^{+}U^{*}=\sum _{i=1}^{r}\sigma _{i}^{-1}\,v_{i}\,u_{i}^{*},$

де

Σ⁺ — матриця утворена транспонуванням Σ і заміною всіх її ненульових діагональних елементів на обернені.

Зв'язок SVD з ортогонально-проєкційними матрицями

• $\ P(M)\equiv M^{+}M=\sum _{i=1}^{r}v_{i}\,v_{i}^{*}=\sum _{i=1}^{r}P(v_{i})$ — розклад ортогонально-проєкційної матриці(проєктора) в суму проєкторів,
• $\ P(M^{*})\equiv MM^{+}=\sum _{i=1}^{r}u_{i}\,u_{i}^{*}=\sum _{i=1}^{r}P(u_{i}).$

Див. також

• Теорія матриць
• Розклад матриці
• Метод найменших квадратів
• Метод головних компонент

Джерела

• Гантмахер Ф. Р. Теорія матриць. — 2024. — 703 с.(укр.)
• Ланкастер П.. Теория матриц. — 2. — Москва : Наука, 1982. — 272 с.(рос.)
• Р.Хорн, Ч.Джонсон. Матричный анализ. — М: : Мир, 1989. — 653 с.(рос.)
• Gene H. Golub, Charles F. Van Loan. Matrix Computations. — 4. — М: : The Johns Hopkins University Press, 2013. — 756 с.(англ.)