Гранування (геометрія)

Зірчастий октаедр як результат гранування куба

У геометрії гранування — процес видалення частини многокутника або многогранника без утворення нових вершин.

Гранування є оберненим або двоїстим до ззірчення: для кожної зірчастої форми деякого опуклого многогранника існує двоїсте гранування двоїстого многогранника.

Ограновані багатокутники

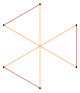
Наприклад, правильний п'ятикутник має одне симетричне гранування, пентаграму, а правильний шестикутник — два симетричні гранування: одне з них — многокутник, а інше — з'єднання двох трикутників.

Опуклі
Правильний п'ятикутник {5}	Правильний шестикутник {6}
Правильні	Квазіправильні	Правильні з'єднання
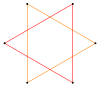
Пентаграма {5/2}	Зірчастий шестикутник	Гексаграма {6/2}

Ограновані багатогранники

Правильний ікосаедр можна огранувати до трьох правильних многогранників Кеплера — Пуансо — малого зірчастого додекаедра, великого додекаедра і великого ікосаедра. Вони мають 30 ребер.

Опуклі	Правильні зірки
Ікосаедр	Великий додекаедр	Малий зірчастий додекаедр	Великий ікосаедр

Правильний додекаедр можна огранувати до одного правильного многогранника Кеплера — Пуансо, трьох однорідних зірчастих многогранників і трьох з'єднань многогранників. Однорідні зірки і з'єднання п'яти кубів будуються на діагоналях граней. Виїмчастий додекаедр є огрануванням із зірчастими октаграмними гранями.

Опуклі	Правильні зірки	Однорідні зірки			Вершинно-транзитивні
Додекаедр	Великий зірчастий додекаедр	Малий бітригональний ікосододекаедр	Бітригональний додекаедр	Великий бітригональний ікосододекаедр	Виїмчастий додекаедр

Опуклі	Правильні з'єднання
Додекаедр	П'ять тетраедрів	П'ять кубів	десять тетраедрів

Історія

Гранування вивчалося не настільки інтенсивно, як ззірчення.

• 1619 року Кеплер описав правильне з'єднання двох тетраедрів, укладених в куб, яке назвав Stella octangula. Схоже, це перший відомий приклад гранування.
• 1858 року Бертран отримав правильні зірчасті многогранники (тіла Кеплера — Пуансо), огранувавши правильні опуклі ікосаедр і додекаедр.
• 1974 року Бридж перерахував кілька огранувань правильних многогранників, зокрема, огранування додекаедра.
• 2006 року Інчибальд описав базову теорію діаграм гранування для многогранників. Для заданої вершини діаграма показує можливі ребра і фасети (нові грані), які можна використати для гранування початкової оболонки. Ця діаграма двоїста діаграмі ззірчення двоїстого многогранника, яка показує всі можливі ребра та вершини для деякої площини грані початкового ядра.

Література

• J. Bertrand. Note sur la théorie des polyèdres réguliers // Comptes rendus des séances de l'Académie des Sciences. — 1858. — Т. 46 (10 листопада). — С. 79—82.
• N. J. Bridge. Facetting the dodecahedron // Acta crystallographica. — 1974. — Т. A30 (10 листопада). — С. 548—552.
• G. Inchbald. Facetting diagrams // The mathematical gazette. — 2006. — Т. 90 (10 листопада). — С. 253—261.
• Alan Holden. Shapes, Space, and Symmetry. — New York : Dover, 1991. — Т. 94.

Посилання

• Weisstein, Eric W. Faceting(англ.) на сайті Wolfram MathWorld.
• Джордж Ольшевський. Faceting на Glossary for Hyperspace