Великий додекаедр
| Великий додекаедр | |
|---|---|

| |
| Тип | Тіло Кеплера — Пуансо |
| Зірчаста форма | Правильного додекаедра |
| Властивості | Неопуклий, рівносторонній, правильний зірчастий багатогранник, гране-транзитивний, вершинно-транзитивний. |
| Комбінаторика | |
| Елементи | 12 граней; 30 ребер; 12 вершин (5-го степеня). |
| Грані {p} |
12 прав. п'ятикутників = 12 {5}. |
| Характеристика Ейлера |
|
| Конфігурація вершини | (5.5.5.5.5)/2 = (55)/2 [1] |
| Конфігурація грані | V(5/2)5 |
| Вершинна фігура | 12 Правильних пентаграм {5/2} [2] :стор.435 ;[3]  , , 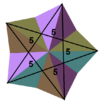 з довжиною сторони |
| Щільність[en] | 3 |
| Рід | 4 |
| Класифікація | |
| Позначення |
• W21 (в нотації М. Веннінґера) [4] |
| Символ Шлефлі {p, q} |
{5, 5/2} |
| Діаграма Коксетера — Динкіна | |
| Символ Витгоффа[en] |
5/2 | 2 5 |
| Група симетрії |
Ih[en], H3, [5,3], (*532), порядок 120 |
| Двоїстий багатогранник | |
| Розгортка | 
|
Великий додекаедр [5] [2] [6] — один з чотирьох правильних зірчастих багатогранників Кеплера — Пуансо.
Цей багатогранник було відкрито у 1809 році Луї Пуансо[7] ; [8] , а назву йому дав Артур Кейлі в 1859 році. [2]
Він складається з 12 граней — правильних п'ятикутників (шість пар п'ятикутних граней лежать в паралельних площинах), по 5 п'ятикутників у кожній вершині, що перетинаються між собою. Має 12 вершин, кожна з яких є вершиною зірчастого п'ятигранного кута.
Його символ Шлефлі — . [2]
Має центральну ділянку кожної грані у вигляді п'ятипроменевої зірки (пентаграми), «приховану» всередині багатогранника, при цьому зовні видно тільки ділянки граней у вигляді рівнобедрених трикутників. Частина граней, що знаходиться всередині багатогранника відіграє роль плоскої мембрани та не розмежовує внутрішній простір багатогранника.
Розташування вершин[en] (опукла оболонка) великого додекаедра, а також розташування його ребер таке ж як і у правильного ікосаедра.
Великий додекаедр має повну симетрію правильного ікосаедра, і отже, всі його елементи симетрії, а саме:
1) має 31 вісь обертової симетрії:
‒ 6 осей 5-го порядку — проходять через протилежні вершини;
‒ 10 осей 3-го порядку — проходять через протилежні точки, в яких перетинаються три грані («вістря тригранних виїмок»);
‒ 15 осей 2-го порядку — проходять через середини протилежних паралельних ребер.
2) має 15 площин дзеркальної симетрії, що проходять через вершину та середину протилежного ребра для кожної грані.
3) має центр симетрії.

|

|

|
| Діаграма ззірчення правильного додекаедра та грань великого додекаедра на ній | Жовтим кольором зображено грань великого додекаедра (частина грані прихована всередині багатогранника) | Утворення грані великого додекаедра |
Великий додекаедр є другою зірчастою формою правильного додекаедра. Його грані складені з нульового, першого та другого відсіків на діаграмі ззірчення правильного додекаедра. [5]
Великий додекаедр утворюється з правильного додекаедра при продовженні (розширенні) його граней (кожна грань правильного додекаедра розширюється до її взаємного перетину з п'ятьма не суміжними до неї гранями), тобто кожна грань α правильного додекаедра замінюється правильним п'ятикутником, описаним навколо п'ятикутної зірки з ядром α.[6]
Також великий додекаедр є радіально-опуклим зірчастим багатогранником, тобто кожен промінь, що виходить з його центра, перетинає багатогранник лише в одній точці.[9] ; [8]

Великий додекаедр має таке саме розташування ребер та розташування вершин[en] , як і опуклий правильний ікосаедр, тобто опукла оболонка великого додекаедра є правильним ікосаедром.
Поєднання правильного ікосаедра та великого додекаедра утворює вироджений зірчастий багатогранник малий складений ікосододекаедр[en].Він має подвоєні (продубльовані) ребра, що і робить його виродженим.
Багатогранник, візуально схожий на великий додекаедр, з довжиною ребра можна отримати з правильного ікосаедра з довжиною ребра , наростивши на його гранях (але не назовні, а всередину тіла), правильні трикутні піраміди, висотою .[10] Фактично відбувається не нарощення пірамід, а видалення їх з тіла ікосаедра. Але отриманий таким чином багатогранник схожий на великий додекаедр тільки візуально, але насправді ним не є, оскільки має додаткові вершини та ребра, що належать цим пірамідам.
Отриманий таким чином багатогранник (з увігнутими пірамідами) топологічно ідентичний до триакіс ікосаедра.
У всіх формулах нижче: — відношення пропорції «золотого перетину». (послідовність A001622 з Онлайн енциклопедії послідовностей цілих чисел, OEIS).
| Для великого додекаедра з довжиною ребра : | ||
|---|---|---|
| Висота «зірчастої піраміди»
над гранню великого додекаедра |
≈ 0.5257311121 | |
| Радіус описаної сфери
(проходить через всі вершини) |
≈ 0.951056516 | |
| Радіус напіввписаної сфери
(дотикається до всіх ребер) |
≈ 0.809016994 | |
| Радіус вписаної сфери
(дотикається до всіх граней) |
≈ 0.425325404 | |
| Площа поверхні | ≈ 10.89813792 | |
| Об'єм | ≈ 1.545084972 | |
| Двогранний кут між гранями | ≈ 1.1071487 рад
≈ 63°26′ 5.81576′′ | |
Центр мас великого додекаедра знаходиться в його геометричному центрі.
Момент інерції суцільного великого додекаедра з масою m та довжиною ребра a (вісь обертання проходить через протилежні вершини):[11]
Як було зазначено вище, великий додекаедр має таке ж розташування вершин, як і правильний ікосаедр, а отже, вершини великого додекаедра з довжиною ребра та правильного ікосаедра в декартовій системі координат збігаються та мають наступні координати:
При цьому вершини (окрім двох діаметрально протилежних вершин на осі Oz) лежать в двох паралельних площинах (паралельних до площини Oxy), в кожній з яких розташовані як вершини правильного п'ятикутника.
Початок координат збігається з центром багатогранника, що є його центром симетрії та центром вписаної, напіввписаної та описаної сфер.
Вісь Oz збігається з однією з осей симетрії 5-го порядку, а вісь Oy — з однією з осей симетрії 2-го порядку.
Площина Oxz є однією з площин симетрії багатогранника.
Також, великий додекаедр з довжиною ребра в декартовій системі координат має вершини з наступними координатами:
При цьому вершини лежать в чотирьох паралельних площинах (паралельних до площини Oxy), в кожній з яких розташовані як вершини правильного трикутника.
Початок координат збігається з центром багатогранника. Вісь Oz збігається з однією з осей симетрії 3-го порядку, а вісь Oy — з однією з осей симетрії 2-го порядку. Площина Oxz є однією з площин симетрії багатогранника.

Існує чотири неопуклих однорідних багатогранники, що утворені певними ступенями операції зрізання великого додекаедра.
Зрізаний великий додекаедр[en] є однорідним неопуклим багатогранником U37, що має діаграму Коксетера — Динкіна ![]()
![]()
![]()
![]()
![]()
![]()
![]() та символ Шлефлі t{5,5/2}. Має 24 граней (12 п'ятипроменевих зірок (пентаграм) та 12 правильних десятикутників), 90 ребер та 60 вершин.[12]
та символ Шлефлі t{5,5/2}. Має 24 граней (12 п'ятипроменевих зірок (пентаграм) та 12 правильних десятикутників), 90 ребер та 60 вершин.[12]
Додекадодекадр[en] утворюється при повному зрізанні[en] (ректифікації) великого додекаедра, коли зрізання вершин проводиться до точок, що лежать на серединах ребер багатогранника, тобто ребра початкового багатогранника фактично зникають.Він є однорідним неопуклим багатогранником U36. Має 24 граней (12 п'ятипроменевих зірок (пентаграм) та 12 правильних п'ятикутників), 60 ребер та 30 вершин.
Процес подальшого зрізання призводить до появи зрізаного малого зірчастого додекаедра, що є виродженим однорідним багатогранником. Візуально він виглядає як правильний додекаедр, але має 24 подвійно-накриті грані.
Процес зрізання великого додекаедра завершується (при повному глибокому зрізанні або біректифікації) утворенням двоїстого до нього багатогранника — малого зірчастого додекаедра, коли грані початкового багатогранника зменшуються до точок, тобто фактично зникають.
| Назва | Великий додекаедр | Зрізаний великий додекаедр | Додекадодекадр[en] | Зрізаний малий зірчастий додекаедр | Малий зірчастий додекаедр |
|---|---|---|---|---|---|
| Діаграма Коксетера — Динкіна | x5o5/2o |
o5o5/2x |
o5x5/2o |
x5x5/2o |
o5x5/2x |
| Символ Шлефлі | {5,5/2} | t{5,5/2} | r{5,5/2} | t{5/2,5} | {5/2,5} |
| Зображення | 
|

|

|

|

|
Родина зірчастих форм правильного додекаедра.
| Зірчасті форми правильного додекаедра | ||||
|---|---|---|---|---|
| Тіло Платона | Тіла Кеплера — Пуансо | |||
| Додекаедр | Малий зірчастий додекаедр | Великий додекаедр | Великий зірчастий додекаедр | |
| Символ Шлефлі
{p, q} |
{5,3} | {5/2,5} | {5,5/2} | {5/2,3} |
| Зображення | 
|

|

|

|
| Діаграма | 
|

|

|

|
| Обертання | 
|

|

|

|

Два однорідних з'єднання багатогранників складаються з великих додекаедрів:
| З'єднання двох великих додекаедрів | З'єднання п'яти великих додекаедрів |
|---|---|

|

|
| Обертання багатогранника | Сферична проєкція | Розгортка | Модель багатогранника з дроту |
|---|---|---|---|

|
 Цей багатогранник також можна подати у вигляді сферичної плитки зі щільністю 3. (Одна сферична п'ятикутна грань, обведена синім і заповнена жовтим кольорами) |
 × 20 × 20 Великий додекаедр можна скласти з паперу, з'єднавши разом 20 правильних трикутних пірамід (без основи). Кожен рівнобедрений трикутник (золотий гномон) в цій розгортці візуально представляє видиму частину правильного п'ятикутника — грані великого додекаедра. |

|
| Багатокутник Петрі[en] великого додекаедра | ||||
|---|---|---|---|---|

|

| |||
| Просторовими багатокутниками Петрі[en] Великого додекаедра є 10 просторових шестикутників. | ||||
- Однорідний зірчастий многогранник
- Зірка Александера
- З'єднання малого зірчастого додекаедра та великого додекаедра[en]
- ↑ Robert Webb. Great Dodecahedron. software3d.com.
- ↑ а б в г д H. S. M. Coxeter, 1954.
- ↑ Gratrix.net - Uniform Polyhedra Summary. web.archive.org (англ.) . Архів оригіналу за 10 листопада 2017.
- ↑ Wenninger.
- ↑ а б Magnus J. Wenninger, 1975.
- ↑ а б Александров П. С., Маркушевич А. И., Хинчин А. Я. (1963), Энциклопедия элементарной математики (ru) , т. IV., м-ква: гифмл, с. 443—444
- ↑ Louis Poinsot, 1810, с. 16—48.
- ↑ а б Richeson, D.S., 2008.
- ↑ Weisstein, Eric W. Fully Supported Stellation. mathworld.wolfram.com (англ.). Процитовано 8 травня 2024.
- ↑ Weisstein, Eric W. Great Dodecahedron. mathworld.wolfram.com (англ.). Процитовано 9 травня 2024.
- ↑ Great dodecahedron inertia tensor - Wolfram Alpha. www.wolframalpha.com (англ.) .
- ↑ Maeder, Roman. 37: truncated great dodecahedron. MathConsult.
- Wenninger, Magnus (1974). Polyhedron Models [Моделі багатогранників] (англ.) . Cambridge University Press. ISBN 0-521-09859-9.
- Magnus J. Wenninger (1975). Polyhedron Models for the Classroom. (PDF) (англ.) . № Вид. 2-ге. National Council of Teachers of Mathematics, Inc.,Reston, Va. с. 64.
- H. S. M. Coxeter. Uniform polyhedra / M. S. Longuet-Higgins, J. C. P. Miller // Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. — The Royal Society, 1954. — Т. 246, № 916. — С. 401—450. — ISSN 0080-4614. — DOI:.
- Louis Poinsot. Memoire sur les polygones et polyèdres. — J. de l'École Polytechnique. — 1810. — Т. 9. — P. 16-48.
- Richeson, D.S. (2008). Euler's Gem: The Polyhedron Formula and the Birth of Topology. Princeton University Press. с. 151. ISBN 9780691126777. LCCN 2008062108.
- H. S. M. Coxeter. Star polytopes and the Schläfli function f(α,β,γ) // Elemente der Mathematik. — 1989. — Vol. 44, iss. 2. — P. 25-36. — ISSN 0013-6018.
- Arthur Cayley. The Collected Mathematical Papers. — Richmond, Surrey : Garden House, Cambridge, 1891. — Т. 4. — С. 82-87. — (On Poinsot’s Four New Regular Solids (розділ 241-242 ))
- J. Conrad, C. Chamberland, N. P. Breuckmann, B. M. Terhal (13 липня 2018). The small stellated dodecahedron code and friends. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences (англ.). 376 (2123): 20170323. doi:10.1098/rsta.2017.0323. ISSN 1364-503X. PMC 5990658. PMID 29807900. Архів оригіналу за 20 серпня 2021.
{{cite journal}}: символ нерозривного пробілу в|author=на позиції 48 (довідка)Обслуговування CS1: Сторінки з PMC з іншим форматом (посилання) - Cayley, Arthur (1859). XIX. On Poinsot's four new regular solids. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. Taylor & Francis. 17 (112): 123—128.
- Weisstein, Eric W. Great Dodecahedron(англ.) на сайті Wolfram MathWorld.
- Weisstein, Eric W. Dodecahedron Stellations(англ.) на сайті Wolfram MathWorld.
- Great dodecahedron(англ.) на сайті Polytope Wiki.
- Great Dodecahedron (англ.) на сайті dmccooey.com.
- Nan Ma. «Great dodecahedron {5, 5/2}»
- Klitzing, Richard. «gad» (англ.)
- Однорідні багатогранники та двоїсті до них (англ.)
- Stellation and facetting — a Brief History (англ.)
- Paper Great Dodecahedron



































