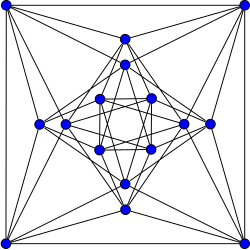
Граф Шрікханде

Граф Шрікханде
Названо на честь	Ш. Ш. Шрікханде
Вершин	16
Ребер	48
Радіус	2
Діаметр	2
Обхват	3
Автоморфізм	192
Хроматичне число	4
Хроматичний індекс	6
Число черг	3
Властивості	сильно регулярний гамільтонів симетричний ейлерів цілий

Граф Шрікханде — граф, знайдений Ш. Ш. Шрікханде 1959 року. Граф сильно регулярний, має 16 вершин і 48 ребер і кожна вершина має степінь 6. Кожна пара вузлів має рівно двох спільних сусідів, незалежно від того, пов'язана ця пара ребром чи ні.

Побудова

Граф Шрікханде можна побудувати як граф Келі, в якому множина вершин — це $\mathbb {Z} _{4}\times \mathbb {Z} _{4}$, а дві вершини пов'язані тоді й лише тоді, коли різниця міститься в $\{\pm (1,0),\pm (0,1),\pm (1,1)\}$ .

Властивості

У графі Шрікханде будь-які дві вершини I і J мають двох різних спільних сусідів (за винятком самих вершин I і J), що виконується незалежно від того, суміжні I і J, чи ні. Іншими словами, граф сильно регулярний та його параметрами є: {16,6,2,2}, тобто $\lambda =\mu =2$. З цієї рівності випливає, що граф асоційований із симетричними зрівноваженими неповними блок-схемами (англ. Balanced Incomplete Block Designs, BIBD). Такі ж параметри має 4×4 туровий граф, тобто реберний граф L(K_4,4) повного двочасткового графа K_4,4. Останній граф є єдиним реберним графом L(K_{n, n}), якого параметри сильної регулярності не визначають єдиним чином, і граф ділить їх з іншим графом, а саме графом Шрікханде (який не є туровим графом).

Граф Шрікханде локально шестикутний. Тобто сусіди кожної вершини утворюють цикл із шести вершин. Як і будь-який локально циклічний граф, граф Шрікханде є 1-вимірним кістяком тріангуляції Вітні деякої поверхні. У разі графа Шрікханде ця поверхня — тор, у якому кожна вершина оточена шістьма трикутниками. Таким чином, граф Шрікханде — це тороїдальний граф. Вкладення утворює регулярне відображення в тор з 32 трикутними гранями. Кістяк дуального графа цього відображення (як вкладеного в тор) — граф Діка, кубічний симетричний граф.

Граф Шрікханде не є дистанційно-транзитивним. Це найменший дистанційно-регулярний граф, який не є дистанційно-транзитивним.

Група автоморфізмів графа Шрікханде має порядок 192. Вона діє транзитивно на вершини, на ребра та дуги графа. Тому граф Шрікханде є симетричним графом.

Характеристичний многочлен графа Шрікханде дорівнює $(x-6)(x-2)^{6}(x+2)^{9}$. Отже, граф Шрікханде є цілим графом — його спектр складається повністю з цілих чисел.

Граф має книжкову товщину 4 та число черг 3 .

Галерея

• 
  Граф Шрікханде є тороїдальним.
• 
  Хроматичне число графа Шрікханде дорівнює 4.
• 
  Хроматичний індекс графа Шрікханде дорівнює 6.
• 
  Граф Шрікханде, намальований симетрично.
• 
  Граф Шрікханде гамільтонів.

Див. також

• Графи Чана

Література

• Shrikhande S. S. The uniqueness of the L₂ association scheme // Annals of Mathematical Statistics. — 1959. — Т. 30. — С. 781–798. — DOI:10.1214/aoms/1177706207.
• Frank Harary. Graph Theory. — Massachusetts : Addison-Wesley, 1972.
  • Харари Ф. Теория графов. — М. : Мир, 1973.
• , Cambridge University Press, ISBN 0-521-43594-3 {{citation}}: Пропущений або порожній |title= (довідка)
• Brouwer A. E., Cohen A. M., Neumaier A. Distance-Regular Graphs. — New York : Springer-Verlag, 1989. — С. 104–105, 136.
• Jessica Wolz. Engineering Linear Layouts with SAT. — University of Tübingen, 2018. — (Master Thesis)

Посилання

• The Shrikhande Graph Пітер Кемерон (Peter Cameron), серпень 2010. Архівовано листопад 24, 2010 на сайті Wayback Machine.