Дерево Тремо
Де́рево Тремо́ неорієнтованого графа G — це кістякове дерево графа G з виділеним коренем зі властивістю, що будь-які дві суміжні вершини в графі G пов'язані відношенням предок/нащадок. Всі дерева пошуку в глибину і всі гамільтонові шляхи є деревами Тремо. Дерева Тремо названо на честь Чарльза П'єра Тремо, французького автора XIX століття, який використовував варіант пошуку в глибину як стратегію виходу з лабіринта[1][2]. Дерева Тремо також називають норма́льними кістяко́вими дере́вами, особливо в контексті нескінченних графів[3].
У скінченних графах, хоча пошук у глибину сам по собі спочатку послідовний, дерева Тремо можна побудувати рандомізованим паралельним алгоритмом із класом складності RNC. Дерева Тремо можна використовувати для визначення деревної глибини графа і як частину критерію планарності[en] для перевірки, чи є граф планарним. Опис дерев Тремо одномісною логікою графів[en] другого порядку дозволяє ефективно розпізнати властивості графа, залежні від орієнтації, для графів з обмеженою деревною шириною за використання теореми Курселя.
Не кожен нескінченний граф має дерево Тремо і графи, які такого дерева не мають, можна описати забороненими мінорами. Дерево Тремо існує в будь-якому графі зі зліченним числом вершин, навіть якщо варіант нескінченного пошуку в глибину не може успішно перевірити всіх вершин графа. У нескінченному графі дерево Тремо повинне мати рівно один нескінченний шлях для кожного кінця графа і існування дерева Тремо характеризує графи, топологічні поповнення яких, утворені доданням нескінченно віддаленої точки для кожного променя, є метричними просторами.
У графі, показаному нижче, дерево з ребрами 1-3, 2-3 і 3-4 є деревом Тремо, якщо його коренем призначити вершину 1 або вершину 2 — будь-яке ребро графа належить дереву, за винятком ребра 1-2, яке (при виборі зазначеного кореня) з'єднує пару предок-нащадок.
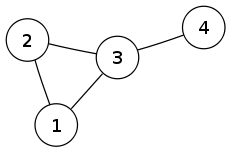
Однак, якщо вибрати за корінь для того ж дерева вершину 3 або вершину 4, отримаємо кореневе дерево, яке не є деревом Тремо, оскільки з цими коренями вершини 1 і 2 вже не будуть предком/нащадком.
Будь-який скінченний зв'язний неорієнтований граф має щонайменше одне дерево Тремо. Можна побудувати таке дерево за допомогою пошуку в глибину і з'єднання кожної вершини (відмінної від початкової вершини пошуку) з ранішою вершиною, з якої отримано доступ до поточної вершини. Дерево, побудоване так, відоме як дерево пошуку в глибину. Якщо uv є довільним ребром у графі і u є ранішою з двох вершин, досягнутих під час пошуку, тоді v повинна належати піддереву нащадків u в дереві пошуку в глибину, оскільки пошук обов'язково виявить вершину v, переглядаючи це дерево або з однієї з вершин піддерева, або безпосередньо з вершини u. Будь-яке скінченне дерево Тремо можна утворити як дерево пошуку в глибину — якщо T є деревом Тремо скінченного графа і пошук у глибину досліджує нащадків T кожної вершини перед розглядом будь-якої іншої вершини, це обов'язково генерує T як дерево пошуку в глибину графа.
Задача пошуку дерева Тремо є P-повною[en], якщо шукати за допомогою послідовного алгоритму пошуку в глибину, в якому сусіди кожної вершини переглядаються в порядку їх номерів[4]. Проте, можна знайти інше дерево Тремо, скориставшись рандомізованим паралельним алгоритмом, що показує належність побудови дерев Тремо до класу складності RNC[5]. Залишається невідомим, чи можна побудувати дерево Тремо детермінованим паралельним алгоритмом, що належить до класу NC[6].
Можна виразити властивість, що множина T ребер з вибраною кореневою вершиною r утворює дерево Тремо, в одномісній логіці графів[en] другого порядку, і такий вираз називають MSO2. Цю властивість можна виразити як поєднання таких властивостей:
- Граф пов'язаний ребрами з T. Це можна виразити логічно як твердження, що для будь-якої непорожньої власної підмножини вершин графа існує ребро в T, що має рівно одну кінцеву точку в цій підмножині.
- T ациклічна. Це можна виразити логічно як твердження, що не існує непорожньої підмножини C множини T, для якої кожна вершина має або нуль, або два ребра з C.
- Будь-яке ребро e, що не належить T, з'єднує пару предок/нащадок вершин у T. Це істинне, коли обидва кінці ребра e належать шляху в T. Це можна висловити логічно як твердження, що для всіх ребер e існує підмножина P множини T, така, що рівно дві вершини, одна з яких r, інцидентні одному ребру в P, і обидва кінці дуги e інцидентні принаймні одному ребру в P.
Як тільки дерево Тремо ідентифіковано таким способом, можна описати орієнтацію даного графа в одномісній логіці другого порядку, вказавши множини ребер, які орієнтовані від предка до нащадка. Ребра, що не належать цій множині, мають бути орієнтовані в зворотному напрямку. Ця техніка дозволяє описати властивості графа, що використовують орієнтацію, в одномісній логіці другого порядку, що дозволяє перевірити ці властивості ефективно на графах із обмеженою деревною шириною за допомогою теореми Курселя[7].
Якщо граф має гамільтонів шлях, то цей шлях (з коренем як одним з його кінців) є також деревом Тремо. Множина неорієнтованих графів, для яких будь-яке дерево Тремо має такий вигляд, складається з циклів, повних графів і збалансованих повних двочастинних графів[8].
Дерева Тремо тісно пов'язані з концепцією деревної глибини. Деревну глибину графа G можна визначити як найменше число d, таке, що G можна вкласти у вигляді підграфа графа H, який має дерево Тремо T глибини d. Обмежена глибина дерева в сімействі графів еквівалентна існуванню шляху, який не може з'явитися як мінор графа в сімействі. Багато складних обчислювальних задач на графах мають фіксовано-параметрично розв'язні[en] алгоритми, якщо параметризувати деревною глибиною[9].
Дерева Тремо відіграють також ключову роль у критерії планарності Де Фрейсекса — Розенштіля[en] для перевірки, чи є граф планарним. За цим критерієм граф G планарний, якщо для будь-якого дерева Тремо T графа G решту ребер можна розташувати ліворуч і праворуч від дерева, що запобігає перетину ребер (з цієї причини іноді застосовують назву «ЛП алгоритм» з абревіатурою Лівий/Правий)[10][11].
Не будь-який нескінченний граф має нормальне кістякове дерево. Наприклад, повний граф на незліченній множині вершин не має нормального кістякового дерева — таке дерево в повному графі може бути тільки шляхом, але шлях має лише зліченне число вершин. Однак будь-який граф на зліченній множині вершин має нормальне кістякове дерево[3].
Навіть у зліченних графах пошук у глибину може виявитися неуспішним при перегляді всього графа[3], і не будь-яке нормальне кістякове дерево можна утворити пошуком у глибину — щоб бути деревом пошуку в глибину, зліченне нормальне кістякове дерево повинне мати тільки один нескінченний шлях або один вузол з нескінченним числом сусідів (але не обидва випадки одночасно).
Якщо нескінченний граф G має нормальне кістякове дерево, то його має і будь-який зв'язний мінор графа G. Звідси випливає, що графи, які мають нормальні кістякові дерева, можна описати забороненими мінорами. Один із двох класів заборонених мінорів складається з двочастинних графів, у яких одна частина зліченна, а інша — незліченна, і будь-яка вершина має нескінченний степінь. Інший клас заборонених мінорів складається з певних графів, отриманих із дерев Ароншайна[en][12].
Деталі цього опису залежать від вибору аксіоматики теорії множин, використовуваноїув формалізації математики. Зокрема, в моделях теорії множин, у яких істинна аксіома Мартіна, а континуум-гіпотеза хибна, клас двочастинних графів можна замінити одним забороненим мінором. Однак для моделей, у яких континуум-гіпотеза істинна, цей клас містить графи, які непорівнянні в упорядкуванні мінорів[13].
Нормальні кістякові дерева тісно пов'язані з кінцями нескінченного графа, класами еквівалентності нескінченних шляхів, які йдуть в одному напрямку. Якщо граф має нормальне кістякове дерево, це дерево повинне мати рівно один нескінченний шлях для кожного променя графа[14].
Нескінченний граф можна використати для утворення топологічного простору, якщо розглядати граф сам по собі як симпліційний комплекс і додати нескінченно віддалену точку для кожного променя графа. З такою топологією граф має нормальне кістякове дерево тоді й лише тоді, коли його множину вершин можна розбити на зліченне об'єднання замкнутих множин. Крім того, цей топологічний простір можна подати метричним простором тоді й лиш тоді, коли граф має нормальне кістякове дерево[14].
- ↑ Even, 2011, с. 46–48.
- ↑ Sedgewick, 2002, с. 149–157.
- ↑ а б в Soukup, 2008, с. 193 Theorem 3.
- ↑ Reif, 1985, с. 229–234.
- ↑ Aggarwal, Anderson, 1988, с. 1–12.
- ↑ Karger, Motwani, 1997, с. 255–272.
- ↑ Courcelle, 1996, с. 33–62.
- ↑ Chartrand, Kronk, 1968, с. 696–700.
- ↑ Nešetřil, Ossona de Mendez, 2012, с. 115–144.
- ↑ de Fraysseix, Rosenstiehl, 1982, с. 75–80.
- ↑ de Fraysseix, Ossona de Mendez, Rosenstiehl, 2006, с. 1017–1029.
- ↑ Diestel, Leader, 2001, с. 16–32.
- ↑ Bowler, Geschke, Pitz, 2016.
- ↑ а б Diestel, 2006, с. 846–854.
- Shimon Even. [1] — 2nd. — Cambridge University Press, 2011. — С. 46–48. — ISBN 978-0-521-73653-4. Архівовано з джерела 23 лютого 2017
- Robert Sedgewick. [2] — 3rd. — Pearson Education, 2002. — С. 149–157. — ISBN 978-0-201-36118-6. Архівовано з джерела 11 березня 2022
- Роберт Седжвик. Часть 5. Алгоритмы на графах // Фундаментальные алгоритмы на C. — Москва, Санкт-Петербург, Киев : DiaSoft, 2003. — ISBN 5-93772-083-0.
- John H.Reif. Depth-first search is inherently sequential. — Information Processing Letters. — 1985. — Т. 20. — С. 229–234. — DOI:
- Aggarwal A., Anderson R. J. A random NC algorithm for depth first search // Combinatorica. — 1988. — Т. 8, вип. 1 (2 березня). — С. 1–12. — DOI:.
- David R. Karger, Rajeev Motwani. An NC algorithm for minimum cuts. — SIAM Journal on Computing. — 1997. — Т. 26. — С. 255–272. — DOI:
- Bruno Courcelle. On the expression of graph properties in some fragments of monadic second-order logic // [3] / Neil Immerman, Phokion G. Kolaitis. — Amer. Math. Soc, 1996. — Т. 31. — С. 33–62. — (DIMACS) Архівовано з джерела 21 вересня 2017
- Gary Chartrand, Hudson V. Kronk. Randomly traceable graphs // SIAM Journal on Applied Mathematics. — 1968. — Т. 16 (2 березня). — С. 696–700.
- Jaroslav Nešetřil, Patrice Ossona de Mendez. Chapter 6. Bounded height trees and tree-depth // Sparsity: Graphs, Structures, and Algorithms. — Heidelberg : Springer, 2012. — Т. 28. — С. 115–144. — (Algorithms and Combinatorics) — ISBN 978-3-642-27874-7. — DOI:
- Hubert de Fraysseix, Pierre Rosenstiehl. A depth-first-search characterization of planarity // Graph theory (Cambridge, 1981). — Amsterdam : North-Holland, 1982. — Т. 13. — С. 75–80. — (Ann. Discrete Math.)
- Hubert de Fraysseix, Patrice Ossona de Mendez, Pierre Rosenstiehl. Trémaux trees and planarity // International Journal of Foundations of Computer Science. — 2006. — Т. 17, вип. 5 (2 березня). — С. 1017–1029. — DOI:.
- Lajos Soukup. Infinite combinatorics: from finite to infinite // [4] — Berlin : Springer, 2008. — Т. 17. — С. 189–213. — (Bolyai Soc. Math. Stud.) — ISBN 978-3-540-77199-9. — DOI: Архівовано з джерела 11 березня 2022
- Reinhard Diestel, Imre Leader. Normal spanning trees, Aronszajn trees and excluded minors // Journal of the London Mathematical Society. — 2001. — Т. 63, вип. 1 (2 березня). — С. 16–32. — (Second Series). — DOI:. Архівовано з джерела 10 червня 2007. Процитовано 11 березня 2022.
- Nathan Bowler, Stefan Geschke, Max Pitz. Minimal obstructions for normal spanning trees. — 2016. — 2 березня. — arXiv:1609.01042.
- Reinhard Diestel. End spaces and spanning trees // Journal of Combinatorial Theory. — 2006. — Т. 96, вип. 6 (2 березня). — С. 846–854. — (Series B). — DOI:.
