Зірка (теорія графів)
| Зірка | |
|---|---|
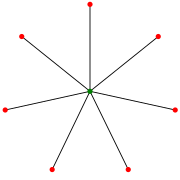 ЗіркаS7. (Деякі автори позначають як S8.) | |
| Вершин | k+1 |
| Ребер | k |
| Діаметр | minimum of (2, k) |
| Обхват | ∞ |
| Хроматичне число | minimum of (2,k+1) |
| Хроматичний індекс | k |
| Spectral Gap | 1 |
| Властивості | Реберно-транзитивний граф Дерево Граф одиничних відстаней Двочастковий |
| Позначення | Sk |
У теорії графів зірка Sk (англ. star) — це повний двочастковий граф K1,k: дерево з єдиним внутрішнім вузлом і k листками (але при k ≤ 1 має k+1 листків і не має внутрішніх вузлів). Крім того, деякі автори визначають Sk як дерево порядку k з максимальною відстанню 2; в цьому випадку зірка k > 2 має k − 1 листок.
Зірка з 3-ма ребрами називається клешнею.
Зірка Sk називається реберно-граціозною[en], коли k парне і не є такою, коли непарне. Вона є реберно-транзитивною сірниковому графу, і має відстань 2 (при k>1), обхват ∞ (не має циклів), хроматичний індекс k і хроматичне число 2 (при k> 0). Крім того, зірка має велику групу автоморфізмів, а саме симетричну групу з k букв.
Зірка також може бути описана, як зв'язний граф, в якому не більше однієї вершини, що має степінь більше одиниці.
Клешні зустрічаються у визначенні графів без клешень, графів, які не мають підграфів з клешнями.[1][2] Крім того, вони є одним з виняткових випадків теореми ізоморфізму графів Вітні: загалом, графи з ізоморфними реберними графами так само є ізоморфними, за винятком клешень і трикутника K3.[3]
Зірка є особливим видом дерева. Як і будь-яке дерево, зірки можуть бути закодовані за допомогою коду Прюфера; послідовність Прюфера для зірки K1,k складається з k-1 копії центральної вершини.[4]
Декілька інваріантів графів визначені в термінах зірок. Арборичність — це мінімальна кількість лісів, які може утворити граф таким чином, що кожне дерево в кожному лісі є зіркою,[5] хроматичним числом зірки[en] називається мінімальне число кольорів, необхідних для фарбування його вершин таким чином, щоб кожні два класи кольорів разом утворювали підграф, у якому всі з'єднані компоненти є зірками.[6] Графи з шириною гілок 1 є саме такими графами, де кожна з'єднана компонента є зіркою.[7]

Множина відстаней між вершинами клешні є прикладом кінцевого метричного простору, який не можна ізометрично вкласти в евклідів простір будь-якої розмірності.[8]
Топологія «Зірка», комп'ютерна мережа змодельована на основі графа-зірки, відіграє важливу роль у розподілених обчисленнях.
Геометрична реалізація графа-зірки формується шляхом визначення ребер з інтервалами деякої фіксованої довжини, використовується як локальна модель кривих у тропічній геометрії. Тропічна крива визначається як метричний простір, що локально ізоморфний як метричний граф зірчастої форми.
За певної нумерації матричне подання графа-зірки може мати форму стріли. Зауважте, як просте перенумерування вершин графа може вплинути на швидкодію алгоритмів. У випадку методу Гауса використання матриці із заповненим верхнім рядком призведе до згубного для швидкодії алгоритму заповнення нульових комірок.
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
| Єдиний внутрішній вузол — перша вершина | Єдиний внутрішній вузол — остання вершина |
- ↑ Faudree, Ralph; Flandrin, Evelyne; Ryjáček, Zdeněk (10 лютого 1997). Claw-free graphs — A survey. Discrete Mathematics. Т. 164, № 1–3. с. 87—147. doi:10.1016/S0012-365X(96)00045-3. Архів оригіналу за 16 березня 2022. Процитовано 27 березня 2016.
- ↑ Chudnovsky, Maria; Seymour, Paul (2005). "The structure of claw-free graphs" (English) . London Math. Soc. Lecture Note Ser. 327: Cambridge: Cambridge Univ. Press. с. 153—171. MR 2187738.
- ↑ Whitney, Hassler (1 січня 1932). Congruent Graphs and the Connectivity of Graphs. American Journal of Mathematics. Т. 54, № 1. с. 150—168. doi:10.2307/2371086. Архів оригіналу за 8 квітня 2016. Процитовано 27 березня 2016.
- ↑ Gottlieb, J.; Julstrom, B. A.; Rothlauf, F.; Raidl, G. R. (2001). "Prüfer numbers: A poor representation of spanning trees for evolutionary search" (English) . Morgan Kaufmann. с. 343—350.
- ↑ Hakimi, S. L.; Mitchem, J.; Schmeichel, E. (22 лютого 1996). Star arboricity of graphs. Discrete Mathematics. Т. 149, № 1–3. с. 93—98. doi:10.1016/0012-365X(94)00313-8. Архів оригіналу за 6 травня 2021. Процитовано 27 березня 2016.
- ↑ Fertin, Guillaume; Raspaud, André; Reed, Bruce (1 листопада 2004). Star coloring of graphs. Journal of Graph Theory (англ.). Т. 47, № 3. с. 163—182. doi:10.1002/jgt.20029. ISSN 1097-0118. Архів оригіналу за 3 травня 2016. Процитовано 27 березня 2016.
- ↑ Robertson, Neil; Seymour, P. D (1 липня 1991). Graph minors. X. Obstructions to tree-decomposition. Journal of Combinatorial Theory, Series B. Т. 52, № 2. с. 153—190. doi:10.1016/0095-8956(91)90061-N. Архів оригіналу за 6 травня 2021. Процитовано 27 березня 2016.
- ↑ Linial, Nathan (2002). "Finite metric spaces–combinatorics, geometry and algorithms" (English) . Proc. International Congress of Mathematicians, Beijing 3. с. 573—586.
