Коефіцієнт Жаккара

Перетин та об'єднання двох множин A та B

Відношення перетину до об'єднання є мірою подібності при виявлянні об'єктів на зображеннях — важливій задачі комп'ютерного зору.

Мі́ра Жакка́ра (коефіціє́нт флористи́чної спі́льності, фр. coefficient de communaute, нім. Gemlinschaftskoefficient) — міра подібності, запропонована Полем Жаккаром в 1901 році. Запропонований метод здобув поширення і нині використовується для оцінки подібності скінченних множин, в інформатиці, для пошуку подібних документів, плагіату тощо.

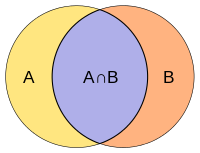
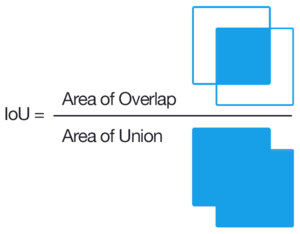
Коефіцієнт Jaccard вимірює подібність між множинами і визначається як міра спільної частини, поділена на міру об'єднання множин:

$J(A,B)={{|A\cap B|} \over {|A\cup B|}}={{|A\cap B|} \over {|A|+|B|-|A\cap B|}}.$

(Коли A та B обидві порожні, тоді J(A,B) = 1.)

$0\leqslant J(A,B)\leqslant 1.$

Відстань Жаккара, яка вимірює відмінність множин, є доповненням коефіцієнта Жаккара до 1 і отримується відніманням коефіцієнта Жаккара від 1, або, еквівалентно, діленням різниці мір об'єднання і перетину двох множин на міру об'єднання:

$d_{J}(A,B)=1-J(A,B)={{|A\cup B|-|A\cap B|} \over |A\cup B|}.$

Інакше можна пояснити відстань Жаккара, як відношення міри симетричної різниці $A\triangle B=(A\cup B)-(A\cap B)$ до об'єднання.

Відстань Жаккара є метрикою на множині всіх скінченних множин.

В ботаніці

Коефіцієнт подібності Жаккара обчислюють за формулою:

$K_{J}={\frac {c}{a+b-c}}$,

де

• а — кількість видів на першому пробному майданчику,
• b — кількість видів на другому пробному майданчику,
• с — кількість видів, спільних для 1-ого та 2-ого майданчиків.

Це перший відомий коефіцієнт подібності. Прізвище автора коефіцієнта в літературі перекладалася як: Жаккард, Джаккард. Коефіцієнт Жаккара в різних модифікаціях і записах активно використовується в екології, геоботаніці, молекулярній біології, біоінформатиці, геноміці, протеїноміці, інформатиці та інших галузях. Міра Жаккара еквівалентна (пов'язані однією монотонно зростаючою залежністю) мірі Серенсена і міру Сокала-Сніта для скінченних множин (множинна інтерпретація):

$K_{1,-1}={\frac {n(A\cap B)}{n(A)+n(B)-n(A\cap B)}}={\frac {n(A\cap B)}{n(A\cup B)}}$

Міру різниці, яка є доповненням до 1 коефіцієнта подібності Жаккара, називають мірою флористичного контрасту.

Для випадку дескриптивних множин (дескриптивна інтерпретація) в екології - це вибірки за рясністю, аналогом вказаної міри є міра Ружички:

$K_{1,-1}={\sum _{i=1}^{r}min(A_{i},B_{i}) \over (\sum _{i=1}^{r}(A_{i})+\sum _{i=1}^{r}(B_{i})-\sum _{i=1}^{r}min(A_{i},B_{i}))}={\sum _{i=1}^{r}min(A_{i},B_{i}) \over \sum _{i=1}^{r}max(A_{i},B_{i}))}$

В конкретних випадках, коли використовуються компоненти булевих векторів, тобто компоненти, які набувають тільки два значення 0 та 1, міра відома під назвою коефіцієнта Танімото або розширеного коефіцієнта Жаккара.

Якщо порівнюються об'єкти за зустрічальністю видів (ймовірнісна інтерпретація), тобто враховуються ймовірності зустрічей, то аналогом міри Жаккара буде ймовірнісна міра Іверсена:

$K_{1,-1}={\frac {P(A\cap B)}{P(A\cup B)}}$.

Для інформаційної аналітичної інтерпретації використовується міра взаємозалежності Райського:

$K_{1,-1}={\frac {I(A,B)}{H(A,B)}}$

Мірою різниці, коеквівалентною мірі подібності Жаккара, є відстань:

$F_{1,-1}=1-{\frac {n(A\cap B)}{n(A)+n(B)-n(A\cap B)}}={\frac {n(A\cup B)-n(A\cap B)}{n(A\cup B)}}$

В інформатиці

В інформатиці коефіцієнт Жаккара двох множин A та В дорівнює відношенню кількості елементів перетину множин до кількості елементів їхнього об'єднання:

$J(A,B)={\frac {|A\cap B|}{|A\cup B|}}$

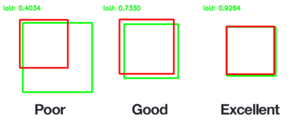
Коефіцієнт Жаккара та алгоритм шинглів використовують для пошуку схожих текстів у великому корпусі документів, а також для виявлення плагіату. Для ефективного обчислення оцінки значення коефіцієнта Жаккара використовують алгоритм MinHash.

Див. також

• Коефіцієнт подібності
• Коефіцієнт Танімото
• В ботаніці:
  • Індекс Соренсена
  • Коефіцієнт Кульчинського (пол. Kulczyński)
  • Коефіцієнт Сімпсона
  • Коефіцієнт Браун-Бланке (розроблений Жозіас Браун-Бланке)
  • Коефіцієнт Охаї
• В ботаніці та кібернетиці:
  • Відстань Геммінга
  • Коефіцієнт Тверського

Посилання

• Індекс Жаккара // Словник-довідник з екології : навч.-метод. посіб. / уклад. О. Г. Лановенко, О. О. Остапішина. — Херсон : ПП Вишемирський В. С., 2013. — С. 101.
• Jaccard's index and species diversity
• Introduction to Data Mining lecture notes from Tan, Steinbach, Kumar [Архівовано 4 Лютого 2012 у Wayback Machine.]
• http://sourceforge.net/projects/simmetrics/ [Архівовано 10 Січня 2013 у Wayback Machine.] SimMetrics a sourceforge implementation of Jaccard index and many other similarity metrics
• Web based tool for comparing texts using Jaccard coefficient