Користувач:Пилипчик/Чернетка
У математичній області Теорії графів, граф Фостер є дводольним.Це 3-регулярний граф з 90 135 вершинами и ребрами.
Граф Фостер є гамільтоновим і має хроматичний номер 2, хроматичний індекс 3, радіус 8, діаметр 8 і розпірку 10. Він також 3-х вершинно зв'язний і 3-реберно зв'язний граф.
Всі кубічні дистанційно-регульовані графи відомі. [2] Граф Фостер є одним з 13 таких графів. Це унікальний дистанційно-транзитивний граф з масивом перетинів {3,2,2,2,2,1,1,1, 1,1,1,1,2,2,2,3}. [3] Це можна побудувати як інцидентність графа часткового лінійного простору, яка є унікальною потрійною кришкою, без 8-кутників узагальненого чотирикутника GQ (2,2). Граф названий на честь Р. М. Фостер. Він виконав перепис кубічних симетричних графів, враховуючи цей графік.
Група автоморфізмів графа Фостер є групою порядку 4320. [4] Він діє транзитивно на вершинах, по краях і на дугах графа. Тому граф Фостер є симетричним. Він має автоморфізм, який бере з однієї будь-якої вершини в будь-яку іншу вершину і будь-який край будь-якого іншого краю. За даними перепису Фостер, граф Фостер, який посилається, як F90A, є єдиним кубічним симетричним графом на 90 вершинах. [5] Характеристичний многочлен графа Foster дорівнює: [2]
.
-
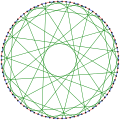
Фостер кольоровий граф, щоб виділити різні цикли
-
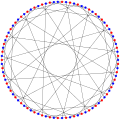
Хроматичне число графа Фостер 2.
-
Хроматичний індекс графа Фостер 3.
- ↑ Weisstein, Eric W. Foster Graph(англ.) на сайті Wolfram MathWorld.
- ↑ Conder, M. and Dobcsányi, P. "Trivalent Symmetric Graphs Up to 768 Vertices."
[[Категорія:Графи, що мають власну назву]] [[Категорія:Регулярні графи]]