Користувач:An-tu/Ізотермічний процес
Ізотермі́чний проце́с (від грец. ísos — рівний, thérme — тепло) — це термодинамічний процес, який відбувається при сталій температурі. Прикладом може бути кипіння рідини або плавлення тіла при сталому тиску.
Щоб здійснити ізотермічний процес, систему розміщують на термостаті (масивне тіло, яке знаходиться у тепловій рівновазі). Оскільки теплопровідність термостату велика, то теплообмін із системою проходить швидко без значної втрати тепла і температура системи майже не відрізняється від температури термостата. Хоча є інші методи, які дозволяють провести ізотермічний процес. Наприклад, за допомогою джерел або стоків тепла. При цьому сталість температури регулюється термометром.
При ізотермічному процесі тиск ідеального газу (ідгаз) обернено-пропорційний до об'єму (див. Закон Бойля-Маріотта).
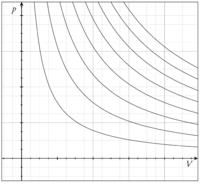
На графіках зображується лініями, які називаються ізотермами. Для ідеального газу на діаграмі тиск-об'єм це гіперболи. В інших параметрах стану, які пов'язують температуру, об'єм і тиск — це прямі лінії. У реальних газах ізотерми можуть мати декілька точок перегину (див. Ізотерми ван дер Ваальса та Ізотерми Амага).
У твердих тілах та більшості рідин при ізотермічному процесі не змінюється об'єм, лише якщо не відбувається фазовий перехід.

Під час ізотермічного процесу система може змінювати свій об'єм. Отже, виконується робота. З визначення механічної роботи знаємо, що:
- ,
де Р — тиск (функція від об'єму), V — об'єм.
З рівняння стану ідеального газу виразимо тиск через об'єм:
- ,
де ν — кількість речовини, R — універсальна газова стала, T — температура (за шаколю Кельвіна).
Тепер підставимо отриману функцію до диференціального рівняння (1):
- .
Щоб отримати повну роботу проінтегруємо останній вираз:
- .
Графічно робота визначається як площа під графіком. Наближено роботу можна визначити як площу трапеції з висотою та основами та . Тоді робота процесу буде:
- .
Оскільки , то вираз (5) спрощується до:
- .
Проте, ця формула є наближеною і буде давати вірні результати при малій зміні об'єму.










