Одна сьома площі трикутника

У евклідовій геометрії трикутник ABC містить трикутник, площа якого становить одну сьому площі ABC, який можна побудувати так: сторони цього трикутника лежать на променях p, q, r, де
- p з'єднує A з точкою на BC, віддаленою від B на третину відстані від B до C,
- q з'єднує B з точкою на CA, віддаленою від C на третину відстані від C до A,
- r з'єднує C з точкою на AB, віддаленою від A на третину відстані від A до B.
Доведення рівності площі одній сьомій площі початкового трикутника випливає з побудови шести паралельних прямих:
- дві паралельні p, одна через C, інша через q.r
- дві паралельні q, одна через A, інша через r.p
- дві паралельні r, одна через B, інша через p.q.
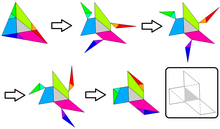
Гуго Штейнгауз запропонував відбити (центральний) трикутник зі сторонами на p, q, r відносно його сторін і вершин.[1] Ці шість додаткових трикутників частково покривають ABC і залишають шість трикутників, що «звисають» за межі ABC. Зважаючи на паралельність під час побудови (як показав Мартін Гарднер у он-лайн журналі Джеймса Ренді), очевидні парні збіги «звисаючих» та відсутніх частин АВС. Як видно з графічного розв'язку, шість відбитих трикутників разом з оригіналом дорівнюють цілому трикутнику ABC.[2]
1859 року цю геометричну побудову та обчислення площі навів у своєму підручнику з евклідової геометрії Роберт Поттс.[3]
За словами Кука та Вуда (2004), цей трикутник спантеличив Річарда Фейнмана під час обідньої розмови; вони надають чотири різні доведення.[4]
Загальніший результат відомий як теорема Рауса.
- ↑ Hugo Steinhaus (1960) Mathematical Snapshots
- ↑ Джеймс Ренді (2001) That Dratted Triangle, доведення Мартіна Гарднера
- ↑ Robert Potts (1859) Euclid's Elements of Geometry, Fifth school edition, задачі 59 і 100, стор. 78 і 80 в Інтернет-архіві
- ↑ R.J. Cook & G.V. Wood (2004) «Feynman's Triangle», Mathematical Gazette 88:299–302
- H. S. M. Coxeter (1969) Introduction to Geometry, стор. 211, John Wiley & Sons.
