Периферійний цикл

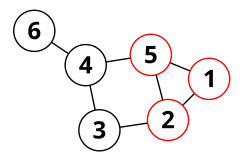
У цьому графі червоний трикутник, утворений вершинами 1, 2 і 5 є периферійним циклом — інші чотири ребра утворюють окремий міст. Однак, п'ятикутник 1-2-3-4-5 не є периферійним, оскільки два ребра, що залишилися, утворюють два окремих мости.

Перифері́йний цикл у неорієнто́ваному гра́фі — цикл, який не відокремлює будь-яку частину графа від будь-якої іншої. Периферійні цикли (або, як їх спочатку називали, периферійні многокутники, оскільки Татт назвав цикли «многокутниками»), першим вивчав Вільям Татт^[1]. Вони відіграють важливу роль в описі планарних графів і в утворенні просторів циклів непланарних графів^[2].

Визначення

Периферійний цикл $C$ у графі $G$ можна визначити формально одним із таких способів:

$C$ є периферійним циклом, якщо він є простим циклом у зв'язному графі з властивістю, за якої для будь-яких двох ребер $e_{1}$ і $e_{2}$ в $G\setminus C$ , існує шлях у $G$ , який починається в $e_{1}$ , закінчується в $e_{2}$ і не має внутрішніх точок, що належать $C$ ^[3].
$C$ є периферійним циклом, якщо він є породженим циклом із властивістю, за якої підграф $G\setminus C$ , утворений видаленням ребер і вершин циклу $C$ , зв'язний.^[4]
Якщо $C$ є будь-яким підграфом графа $G$ , міст^[5] графа $C$ є мінімальним підграфом $B$ графа $G$ , який не має спільних ребер з $C$ і має властивість, за якої всі його точки приєднання (вершини, суміжні ребрам, які належать $B$ і $G\setminus B$ одночасно) належать $C$ ^[6]. Простий цикл $C$ є периферійним, якщо він має рівно один міст^[7]

Легко бачити еквівалентність цих визначень: зв'язний підграф графа $G\setminus C$ (разом із ребрами, що зв'язують його з $C$ ) або хорда циклу, яка порушує породження циклу, в будь-якому випадку має бути мостом, і має бути також клас еквівалентності бінарного відношення на ребрах, у якому два ребра пов'язані, якщо вони є кінцями шляху без внутрішніх вершин у $C$ ^[8]

Властивості

Периферійні цикли з'являються в теорії багатогранних графів, тобто, вершинно 3-зв'язних планарних графів. Для будь-якого планарного графа $G$ і будь-якого планарного вкладення $G$ межі вкладення, породжені циклами, мають бути периферійними циклами. У багатогранному графі всі грані є периферійними циклами і будь-який периферійний цикл є гранню^[9]. Звідси випливає, що (до комбінаторної еквівалентності, вибору зовнішньої грані та орієнтації площини) будь-який багатогранний граф має унікальне планарне вкладення^[10].

У планарних графах простір циклів утворений гранями, але в непланарних графах периферійні цикли відіграють аналогічну роль — для будь-якого вершинно 3-зв'язаного скінченного графа циклічний простір утворюють периферійні цикли^[11]. Результат можна поширити на локально скінченні нескінченні графи^[12]. Зокрема, звідси випливає, що 3-зв'язні графи гарантовано містять периферійні цикли. Існують 2-зв'язні графи, які не містять периферійних циклів (прикладом є повний двочастковий граф $K_{2,4}$ , в якому будь-який цикл має два мости), але, якщо 2-зв'язний граф має мінімальний степінь 3, то він містить принаймні один периферійний цикл^[13].

Периферійні цикли в 3-зв'язних графах можна обчислити за лінійний час, їх використовують для розробки тестів планарності^[14]. Їх також розширено до загальнішого поняття нерозділювальних вушних розкладів. У деяких алгоритмах для перевірки планарності графів корисно знайти цикл, який не є периферійним, з метою розбиття задачі на менші підзадачі. У двозв'язному графі з контурним рангом, меншим від 3, (такому як цикл або тета-граф), будь-який цикл є периферійним, але будь-який двозв'язний граф з контурним рангом 3 і більше має непериферійний цикл, який можна знайти за лінійний час^[15].

Узагальнюючи хордальні графи, Сеймур і Вівер ^[16] визначили стиснутий граф як граф, у якому будь-який периферійний цикл є трикутником. Вони описали ці графи як суми за кліками хордальних графів і максимальних планарних графів^[17].

Пов'язані поняття

Периферійні цикли називали також нерозділювальними циклами^[3], але цей термін двозначний, оскільки він використовується ще для двох інших понять — для простих циклів, видалення яких робить решту графа незв'язною^[18], і для циклів топологічного вкладення графа, таких, що вирізання вздовж циклу не робить незв'язною поверхню, в яку граф укладено^[19].

У матроїдах, нерозділювальний цикл — це цикл матроїда (тобто, мінімальна залежна множина), за якої видалення^[en] циклу залишає менший матроїд, який є зв'язним (тобто, який не можна розбити на пряму суму матроїдів)^[20]. Він аналогічний периферійним циклам, але не тотожний навіть у графових матроїдах^[en] (матроїди, в яких цикли є простими циклами графа). Наприклад, у повному двочастковому графі $K_{2,3}$ будь-який цикл є периферійним (він має лише один міст, шлях із двох ребер), але графовий матроїд, утворений цим мостом не зв'язний, так що ніякий цикл графового матроїда графа $K_{2,3}$ не є нерозділювальним.

Примітки

↑ Tutte, 1963.
↑ Tutte, 1963, с. 743–767.
↑ ^а ^б Di Battista, Eades, Tamassia, Tollis, 1998, с. 74–75.
↑ Це визначення використав Брун (Bruhn, 2004). Однак, Брун відрізняв випадок, що $G$ має ізольовані вершини, від незв'язності, викликаної видаленням циклу $C$ .
↑ Не плутати з мостом, іншим поняттям з такою ж назвою.
↑ Tutte, 1960, с. 304–320.
↑ Це визначення периферійних циклів спочатку використав Татт(Tutte, 1963). Сеймур і Вівер(Seymour, Weaver, 1984) використали таке саме визначення периферійного циклу, але з іншим визначенням моста, яке нагадує визначення породжених циклів для периферійних циклів.
↑ Див., наприклад, теорему 2.4 у статті Татта (Tutte, 1960), яка показує, що множини вершин мостів пов'язані шляхами, див. статтю Сеймур і Вівера (Seymour, Weaver, 1984) для визначення мостів за допомогою хорд і зв'язних компонент, а також статтю Ді Баттіста, Ідса, Тамассіа, Толліса(Di Battista, Eades, Tamassia, Tollis, 1998) для визначення мостів за допомогою класів еквівалентності бінарного відношення на ребрах.
↑ Tutte, 1963, с. Theorems 2.7 и 2.8.
↑ Див. зауваження після теореми 2.8 у статті Татта (Tutte, 1963). Як зауважив Татт, це було вже відомо Вітні (Whitney, 1932)
↑ Tutte, 1963, с. Theorem 2.5.
↑ Bruhn, 2004, с. 235–256.
↑ Thomassen, Toft, 1981, с. 199–224.
↑ Schmidt, 2014, с. 967—978.
↑ Di Battista, Eades, Tamassia, Tollis, 1998, с. 75–76 Lemma 3.4.
↑ Seymour, Weaver, 1984.
↑ Seymour, Weaver, 1984, с. 241–251.
↑ Див., наприклад, (Borse, Waphare, 2008)
↑ Див., наприклад (Cabello, Mohar, 2007)
↑ Maia, Lemos, Melo, 2007, с. 162–171.

Література

Tutte W. T. How to draw a graph // Proceedings of the London Mathematical Society. — 1963. — Т. 13. — С. 743–767. — (Third Series). — DOI:10.1112/plms/s3-13.1.743.
Giuseppe Di Battista, Peter Eades, Roberto Tamassia, Ioannis G. Tollis. Graph Drawing: Algorithms for the Visualization of Graphs. — Prentice Hall, 1998. — С. 74–75. — ISBN 978-0-13-301615-4.
Tutte W. T. Convex representations of graphs // Proceedings of the London Mathematical Society. — 1960. — Т. 10. — С. 304–320. — (Third Series). — DOI:10.1112/plms/s3-10.1.304.
Hassler Whitney^[en]. Non-separable and planar graphs // Transactions of the American Mathematical Society. — 1932. — Т. 34, вип. 2. — С. 339–362. — DOI:10.2307/1989545.
Henning Bruhn. The cycle space of a 3-connected locally finite graph is generated by its finite and infinite peripheral circuits // Journal of Combinatorial Theory. — 2004. — Т. 92, вип. 2. — С. 235–256. — (Series B). — DOI:10.1016/j.jctb.2004.03.005.
Carsten Thomassen, Bjarne Toft. Non-separating induced cycles in graphs // Journal of Combinatorial Theory. — 1981. — Т. 31, вип. 2. — С. 199–224. — (Series B). — DOI:10.1016/S0095-8956(81)80025-1.
Jens M. Schmidt. The Mondshein Sequence // Proceedings of the 41st International Colloquium on Automata, Languages and Programming (ICALP'14). — 2014. — С. 967—978. — DOI:10.1007/978-3-662-43948-7_80.
Seymour P. D., Weaver R. W. A generalization of chordal graphs // Journal of Graph Theory. — 1984. — Т. 8, вип. 2. — С. 241–251. — DOI:10.1002/jgt.3190080206.
Borse Y. M., Waphare B. N. Vertex disjoint non-separating cycles in graphs // The Journal of the Indian Mathematical Society. — 2008. — Т. 75, вип. 1—4. — С. 75–92 (2009). — (New Series).
Sergio Cabello, Bojan Mohar. Finding shortest non-separating and non-contractible cycles for topologically embedded graphs // Discrete and Computational Geometry. — 2007. — Т. 37, вип. 2. — С. 213–235. — DOI:10.1007/s00454-006-1292-5.
Bráulio Maia Junior, Manoel Lemos, Tereza R. B. Melo. Non-separating circuits and cocircuits in matroids // Combinatorics, complexity, and chance. — Oxford : Oxford Univ. Press, 2007. — Т. 34. — С. 162–171. — (Oxford Lecture Ser. Math. Appl.) — DOI:10.1093/acprof:oso/9780198571278.003.0010.

[FOOTNOTETutte1963-1] Tutte, 1963.

[FOOTNOTETutte1963743–767-2] Tutte, 1963, с. 743–767.

[FOOTNOTEDi_Battista,_Eades,_Tamassia,_Tollis199874–75-3] а ^б Di Battista, Eades, Tamassia, Tollis, 1998, с. 74–75.

[4] Це визначення використав Брун (Bruhn, 2004). Однак, Брун відрізняв випадок, що $G$ має ізольовані вершини, від незв'язності, викликаної видаленням циклу $C$ .

[5] Не плутати з мостом, іншим поняттям з такою ж назвою.

[FOOTNOTETutte1960304–320-6] Tutte, 1960, с. 304–320.

[7] Це визначення периферійних циклів спочатку використав Татт(Tutte, 1963). Сеймур і Вівер(Seymour, Weaver, 1984) використали таке саме визначення периферійного циклу, але з іншим визначенням моста, яке нагадує визначення породжених циклів для периферійних циклів.

[8] Див., наприклад, теорему 2.4 у статті Татта (Tutte, 1960), яка показує, що множини вершин мостів пов'язані шляхами, див. статтю Сеймур і Вівера (Seymour, Weaver, 1984) для визначення мостів за допомогою хорд і зв'язних компонент, а також статтю Ді Баттіста, Ідса, Тамассіа, Толліса(Di Battista, Eades, Tamassia, Tollis, 1998) для визначення мостів за допомогою класів еквівалентності бінарного відношення на ребрах.

[FOOTNOTETutte1963Theorems_2.7_и_2.8-9] Tutte, 1963, с. Theorems 2.7 и 2.8.

[10] Див. зауваження після теореми 2.8 у статті Татта (Tutte, 1963). Як зауважив Татт, це було вже відомо Вітні (Whitney, 1932)

[FOOTNOTETutte1963Theorem_2.5-11] Tutte, 1963, с. Theorem 2.5.

[FOOTNOTEBruhn2004235–256-12] Bruhn, 2004, с. 235–256.

[FOOTNOTEThomassen,_Toft1981199–224-13] Thomassen, Toft, 1981, с. 199–224.

[FOOTNOTESchmidt2014967—978-14] Schmidt, 2014, с. 967—978.

[FOOTNOTEDi_Battista,_Eades,_Tamassia,_Tollis199875–76_Lemma_3.4-15] Di Battista, Eades, Tamassia, Tollis, 1998, с. 75–76 Lemma 3.4.

[FOOTNOTESeymour,_Weaver1984-16] Seymour, Weaver, 1984.

[FOOTNOTESeymour,_Weaver1984241–251-17] Seymour, Weaver, 1984, с. 241–251.

[18] Див., наприклад, (Borse, Waphare, 2008)

[19] Див., наприклад (Cabello, Mohar, 2007)

[FOOTNOTEMaia,_Lemos,_Melo2007162–171-20] Maia, Lemos, Melo, 2007, с. 162–171.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]