Стиснутий граф
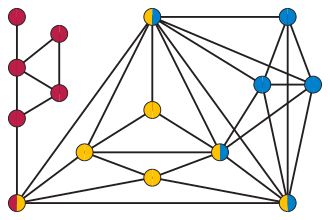
Стиснутий граф — граф, у якому видалення ребер будь-якого породженого циклу з довжиною, більшою трьох, дає незв'язний граф. Тобто це графи, в яких кожен периферійний цикл є трикутником.
У максимальному планарному графі, або, загальніше, в будь-якому поліедральному графі, периферійні цикли точно є гранями планарного вкладення графу, так що поліедральний граф стиснутий тоді і тільки тоді, коли всі грані є трикутниками, або, еквівалентно, він є максимально планарним. Будь-який хордальний граф є стиснутим, оскільки породжені цикли в хордальних графах є тільки трикутниками, так що немає циклів для видалення.
Сума за клікою двох графів утворюється ототожненням двох клік однакового розміру в кожному графі, а потім частина ребер кліки видаляється. Для версії сум за клікою для стиснутих графів крок видалення ребер опускають. Сума за клікою такого типу двох стиснутих графів призводить до іншого стиснутого графу, в якому будь-який довгий породжений цикл у сумі має бути обмеженим однією стороною або іншою (в іншому разі була б хорда між вершинами, яка проходить від однієї сторони суми в іншу), а незв'язні частини на цій стороні, утворені видаленням циклу, мають залишитися несвязними в сумі за клікою. Будь-який хордальний граф можна так розкласти на суму за клікою повних графів, і будь-який максимальний планарний граф можна розкласти на суму за клікою 4-вершинно-зв'язних максимальних планарних графів.
Як показали Сеймур і Вівер[1], це єдино можливі будівельні блоки для стиснутих графів — стиснуті графи, це точно графи, які можна утворити як суми за клікою повних графів і максимальних планарних графів.
- Реберно-досконалий граф, у якому будь-який непарний цикл є трикутником
- Seymour P. D., Weaver R. W. A generalization of chordal graphs // Journal of Graph Theory. — 1984. — Т. 8, вип. 2 (19 січня). — С. 241–251. — DOI:..
