Пилкоподібна хвиля

Обмежена пилкоподібна хвиля: залежність від часу (вгорі) та частоти (внизу). Основна частота складає 220 Гц $(A_{3})$.

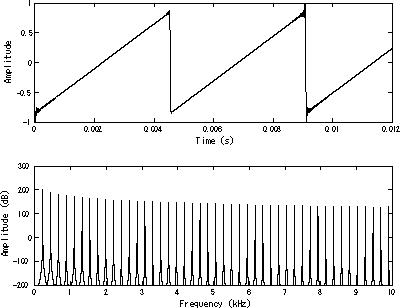
Пилкоподі́бна хви́ля (також пиля́ста або пилча́ста хви́ля) — різновид несинусоїдальної форми хвилі. Її так називають через схожість із зубцями звичайної зубчастої пилки з нульовим кутом попереду.

Подібність полягає в тому, що пилкоподібна хвиля наростає, а потім різко опускається. Однак, у зворотній пилкоподібній хвилі, хвиля падає вниз і потім різко здіймається. Це також можна вважати граничним випадком асиметричної трикутної хвилі.

Кусково-лінійна функція

$x(t)=t-\underbrace {\lfloor t\rfloor } _{\operatorname {floor} (t)}$,

або в еквівалентній формі

$x(t)=t{\pmod {1}}$,

на основі функції цілої частини числа, є прикладом пилкоподібної хвилі з періодом 1.

Більш загальною формою пилкоподібної хвилі на інтервалі від $(-1;1)$ і з періодом $a$ є

$2\left({\frac {t}{a}}-\left\lfloor {\frac {1}{2}}+{\frac {t}{a}}\right\rfloor \right)$.

Ця пилкоподібна функція має ту саму фазу, що і функція синус.

Ще одним прикладом є тригонометрична функція з періодом $p$ та амплітудою $a$:

$y(x)=-{\frac {2a}{\pi }}\arctan \left(\cot \left({\frac {x\pi }{p}}\right)\right)$.

Тоді як прямокутна хвиля побудована лише з непарних гармонік, звук пилкоподібної хвилі різкий і чіткий, а її спектр містить як парні, так і непарні гармоніки основної частоти. Оскільки вона зберігає усі цілі гармоніки, це одна з найкращих форм хвиль, яка використовується для субтрактивного синтезу музичних звуків, особливо смичкових струнних інструментів, таких як скрипки та віолончелі, внаслідок феномену ковзання смичка по струні з пилкоподібним рухом.

Пилкоподібна хвиля може бути побудована за допомогою аддитивного синтезу. Нескінченний ряд Фур'є

$x_{\text{reverse sawtooth}}(t)={\frac {2A}{\pi }}\sum _{k=1}^{\infty }{(-1)}^{k}{\frac {\sin(2\pi kft)}{k}}$

збігається зі зворотною (оберненою) пилкоподібною хвилею. Звичайна пилкоподібна хвиля може бути побудована за допомогою формули

$x_{\mathrm {sawtooth} }(t)={\frac {A}{2}}-{\frac {A}{\pi }}\sum _{k=1}^{\infty }{(-1)}^{k}{\frac {\sin(2\pi kft)}{k}}$,

де $A$ — амплітуда.

У цифровому синтезі цей ряд підсумовується за $k$ таким чином, що найвища гармоніка $N_{\text{max}}$ менша від частоти Найквіста (половина дискретизованої частоти). Цю суму зручніше можна обчислити за допомогою швидкого перетворення Фур'є. Якщо форма хвилі у цифровому вигляді створюється безпосередньо в часовій області за допомогою необмеженої форми, такої як $y=x-$floor($x$), нескінченні гармоніки відбираються, і отриманий тон містить аліасингові спотворення.

Анімація адитивного синтезу пилкоподібної хвилі зі збільшенням кількості гармонік.

Відтворення пилкоподібних звуків при 440Hz $(A_{\text{4}})$, 880Hz $(A_{\text{5}})$ і 1,760Hz $(A_{\text{6}})$ доступна нижче. Представлено обмежений (неаліасинговий) та аліасинговий тони.

Застосування

• Пилкоподібні хвилі відомі завдяки тому, що їх використовують у музиці. Пилкоподібні та прямокутні хвилі є одними з найпоширеніших форм хвиль, що використовуються для створення субтрактивних і віртуальних аналогів музичних синтезаторів;
• Пилкоподібні хвилі застосовуються в імпульсних стабілізаторах напруги. У мікросхемі регулятора сигнал зворотного зв'язку на виході постійно порівнюється з високочастотною пилкоподібною хвилею для створення нового ШІМ-сигналу робочого циклу на виході компаратора.
• Пилкоподібна хвиля є вертикальною та горизонтальною формою сигналів відхилення, які використовуються для генерування растру на екранах ЕПТ телевізорів і моніторів. Осцилографи також застосовують пилкоподібні хвилі для їх горизонтального відхилення, хоча здебільшого вони використовують електростатичне відхилення.
  • На «пандусі» хвилі магнітне поле переміщує електронний промінь поверхнею ЕПТ, створюючи сканувальну лінію;
  • На «обриві» хвилі магнітне поле раптово руйнується, внаслідок чого електронний промінь одразу повертається у положення спокою;
  • Напруга, яка подається на відхильну систему, регулюється різними засобами (трансформаторами, конденсаторами), щоб напруга на півдорозі до «обриву» пилкоподібної хвилі прийняла нульову позначку, тобто від'ємна напруга спричинить відхилення в один напрямок, а додатна — в інший; таким чином, у центрі кріплення відхильної системи може використовуватись вся область екрану для зображення сліду;
  • Система вертикального відхилення працює так само, як і горизонтального, хоч і зі значно меншою частотою (59,94 Гц на NTSC, 50 Гц для PAL і SECAM);
  • Перші телевізійні приймачі керувались самими користувачами, що дозволяло їм коригувати лінійність зображення. Таких засобів керування не було в новіших моделях, оскільки стійкість електронних складників покращилася.

Див. також

Синусоїдна, прямокутна, трикутна та пилкоподібна форми хвиль.

• Список періодичних функцій
• Синусоїдна хвиля
• Прямокутна хвиля
• Трикутна хвиля
• Хвиля
• Звук

Джерела

• Hugh L. Montgomery; Robert C. Vaughan (2007). Multiplicative number theory I. Classical theory. Cambridge tracts in advanced mathematics. Т. 97. с. 536—537. ISBN 978-0-521-84903-6.