Плівка Мебіуса

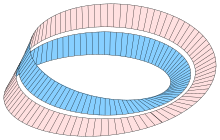
Плівка Мебіуса[1], або крос-кеп (від англ. cross-cap — «перехрещений капелюх»)[2], або схрещений ковпак[3], — деяке вкладення стрічки Мебіуса в тривимірний простір, яке відрізняється від стандартного тим, що при ньому межа стрічки витягнута в коло і її можна заклеїти диском, але при цьому поверхня самоперетинається.
Плівку Мебіуса можна уявити так: візьмемо стрічку і поділимо одну з її меж навпіл; приклеїмо до межі дві блискавки в одному напрямку, зігнемо їх навпіл і застебнемо одну з одною. Вийде поверхня, зображена на картинці: вертикальна лінія — це блискавка, що двічі проходить (спочатку вгору, потім вниз). Зі схеми склеювання неважко побачити, що отримана поверхня гомеоморфна стрічці Мебіуса.
При заклеюванні диска з плівки Мебіуса виходить дійсна проєктивна площина. Справді, стрічку можна розкласти як кільце навколо диска, тоді межа розширеного диска складатиметься з двох застібок, спрямованих однаково; поверхня, що виходить при склеюванні в диска протилежних точок — це і є дійсна проєктивна площина.
- ↑ Дубровин Б. А., Новиков С. П., Фоменко А. Т. Современная геометрия: Методы теории гомологий. — М. : Наука, 1984. — С. 35.
- ↑ Р. Курант, Г. Роббинс. Что такое математика?. — 3-e изд., испр. и доп. — М., 2001. — С. 286. — ISBN 5900916456.
- ↑ Д. П. Ильютко, В. О. Мантуров, И. М. Никонов. Комбинаторная топология и теория графов в задачах и упражнениях. — Ярославль : ЯрГУ, 2013. — С. 8—9. — ISBN 978-5-8397-0980-5.
- Weisstein, Eric W. Плівка Мебіуса(англ.) на сайті Wolfram MathWorld.
