Дійсна проєктивна площина
 Фундаментальний многокутник[en] площини Фундаментальний многокутник[en] площини
|
 Стрічку Мебіуса з єдиним ребром можна замкнути в проєктивну площину, склеївши протилежні краї
|
 Для порівняння, пляшка Клейна — це стрічка Мебіуса, замкнена в циліндр Для порівняння, пляшка Клейна — це стрічка Мебіуса, замкнена в циліндр
|
Дійсна проєктивна площина — приклад компактного неорієнтованого двовимірного многовида, тобто односторонньої поверхні. Проєктивну площину неможливо вкласти у звичайний тривимірний простір без самоперетину. Основна галузь застосування цієї площини — геометрія, позаяк основна побудова дійсної проєктивної площини — простір прямих R3, що проходять через початок координат.
Площину часто описують топологічно в термінах побудови на основі стрічки Мебіуса — якщо склеїти (єдиний) край стрічки Мебіуса із собою в правильному напрямку, отримаємо проєктивну площину (це неможливо здійснити у тривимірному просторі). Еквівалентно, приклеювання круга вздовж межі стрічки Мебіуса дає проєктивну площину. Топологічно, поверхня має ейлерову характеристику 1, бо напіврід (неорієнтований або ейлерів рід) дорівнює 1.
Позаяк стрічку Мебіуса, у свою чергу, можна побудувати з квадрата склеюванням двох його сторін, дійсну проєктивну площину можна подати як одиничний квадрат (тобто [0,1] × [0,1]), у якому сторони ототожнено таким відношенням еквівалентності:
і
- ,
як на лівому малюнку вище.
Проєктивна геометрія не обов'язково стосується кривини і дійсна проєктивну площину можна скрутити й помістити в евклідову площину або тривимірний простір багатьма способами[1]. Деякі важливі приклади вкладення площини описано нижче.
Проєктивну площину не можна вкласти (без перетинів) у тривимірний евклідів простір. Доводиться це приблизно так. Припустимо, що площину вкладено, тоді проєктивна площина обмежує компактну область тривимірного евклідового простору відповідно до узагальненої теореми Жордана. Спрямоване назовні одиничне векторне поле задає тоді орієнтацію межі многовида, проте межею многовида слугує проєктивна площина, яка не орієнтована. Маємо суперечність.
Розглянемо сферу, нехай великі кола сфери будуть «прямими», а пари антиподальних точок[en] будуть «точками». Легко перевірити, що система підпорядковується аксіомам проєктивної площини:
- будь-яка пара різних великих кіл перетинаються в парі антиподальних точок
- будь-які дві різні пари антиподальних точок лежать на єдиному великому колі
Якщо ми ототожнюємо будь-яку точку на сфері з її антиподальною точкою, отримаємо подання дійсної проєктивної площини, в якій «точками» проєктивної площини є реальні точки. Це означає, що проєктивна площина є фактор-простором сфери, отриманим розбиттям сфери на класи еквівалентності відношенням , де якщо . Цей фактор-простір гомеоморфний множині всіх прямих, що проходять через початок координат в R3.
Факторне відображення зі сфери в дійсну проєктивну площину є, фактично, дволистим (тобто два-в-один) накриттям. Звідси випливає, що фундаментальна група дійсної проєктивної площини є циклічною групою порядку 2. За генератор можна взяти цикл AB на малюнку вгорі.
Оскільки сфера покриває дійсну проєктивну площину двічі, проєктивну площину можна подати як замкнуту півсферу, в якої протилежні точки обода ототожнено[2].
Проєктивну площину можна занурити (локальні околи області визначення не мають самоперетинів) у тривимірному просторі. Поверхня Боя є прикладом такого занурення.
Багатогранні приклади повинні мати щонайменше дев'ять граней[3].

Римська поверхня[en] Штейнера є виродженим відображенням проєктивної площини в тривимірний простір, що містить плівку Мебіуса.

Подання у вигляді многогранника — це тетрагемігексаедр[4], який має таку ж загальну форму, що й поверхня Штейнера.
З іншого боку, деякі абстрактні правильні многогранники, напівкуб[en], напівдодекаедр і напівікосаедр, можна побудувати як фігури проєктивної площини. Див. статтю «Проєктивний многогранник[en]».
Описано різні планарні проєкції або відображення проєктивної площини. 1874 року Кляйн описав відображення [1]
Центральна проєкція проєктивної півсфери на площину дає звичайну нескінченну проєктивну площину, описану нижче.
Якщо склеїти круг із плівкою Мебіуса, отримаємо замкнуту поверхню. Цю поверхню можна задати параметрично такими рівняннями:
де u та v пробігають від 0 до 2π. Ці рівняння подібні до рівнянь для тора. На малюнку 1 показано замкнутий диск із плівкою Мебіуса.
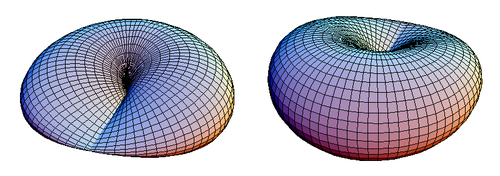
|
| Малюнок 1. Два види диска із плівкою Мебіуса. |
Диск із плівкою Мебіуса має площину симетрії, яка проходить через відрізок із точками перетину (на малюнку площина буде горизонтальною). На малюнку 1 диск із плівкою Мебіуса показано зверху відносно площини симетрії z = 0, але він виглядатиме так само і при розгляді знизу.
Диск із плівкою Мебіуса можна розсікти вздовж площини симетрії з умовою, що не розсікається жодна подвійна точка. Результат наведено на малюнку 2.
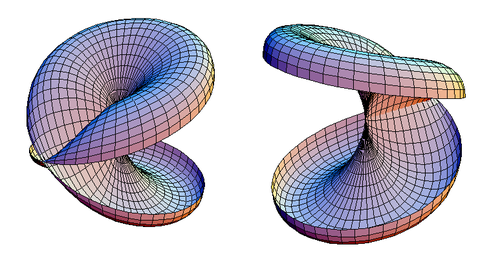
|
| Малюнок 2. Два види розсіченого диска із плівкою Мебіуса. |
За такої умови видно, що розсічений диск із плівкою Мебіуса гомеоморфний самоперетнутому диску, як показано на малюнку 3.
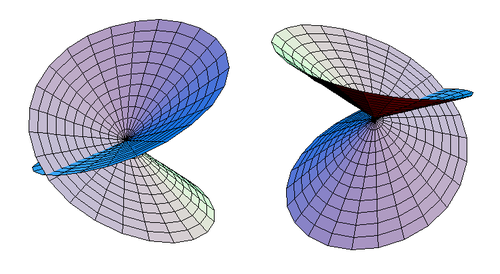
|
| Малюнок 3. Два різних вигляди самоперетнутого диска. |
Самоперетнутий диск гомеоморфний звичайному диску. Параметричні рівняння самоперетнутого диска:
де u пробігає від 0 до 2π, а v — від 0 до 1.
Проєкція самоперетнутого диска на площину симетрії (z = 0 за наведеної вище параметризації), яка проходить тільки через подвійні точки, є звичайним диском, який повторює себе (згортається на себе).
Площина z = 0 розсікає самоперетнутий диск на пару дисків, що є дзеркальними відображеннями один одного. Диски мають центри в початку координат.
Розглянемо тепер ободи дисків (з v = 1). Точки на ободі самоперетнутого диска йдуть парами як відображення одна одної відносно площини z = 0.
Диск із плівкою Мебіуса утворюється ототожненням цих пар точок. Це означає, що точка з параметрами та координатами ототожнюється з точкою , координати якої . Але це означає, що пари протилежних точок на ободі (еквівалентного) звичайного диска ототожнюються. Таким чином, з диска формується дійсна проєктивна площина, так що поверхня, показана на малюнку 1 (диск із плівкою Мебіуса), топологічно еквівалентна дійсній проєктивній площині RP2.
Точки площини можна подати однорідними координатами. Точка має однорідні координати , при цьому координати і відповідають для всіх ненульових значень одній і тій самій точці. Точки з координатами утворюють звичайну дійсну площину, яку називають кінцевою частиною проєктивної площини, а точки з координатами називають точками на нескінченності або ідеальними точками, які утворюють пряму, називану нескінченно віддаленою прямою[en] . Однорідні координати не задають ніякої точки.
Прямі на площині можна задати однорідними координатами. Проєктивна пряма, відповідна площині в R3, має однорідні координати . Таким чином, ці координати мають відношення еквівалентності. для всіх ненульових значень . Це наслідок того, що рівняння тієї ж прямої дає ті самі однорідні координати. Точка лежить на прямій , якщо . Таким чином, прямі з координатами , де і не дорівнюють 0, відповідають прямим звичайної дійсної площини, оскільки вони містять точки, що не лежать на нескінченності. Пряма з координатами є нескінченно віддаленою прямою, оскільки на ній лежать тільки точки, для яких .
Пряму в площині P2 можна задати рівнянням . Якщо ми розглядаємо , і як вектор-стовпець g, а , і як вектор-стовпець x, то наведене вище рівняння можна записати як:
- або .
Скориставшись векторним записом, маємо
- або .
Рівняння (де — ненульовий скаляр) вимітає площину, яка проходить через початок координат R3, а вимітає пряму, яка також проходить через початок координат. Площина і пряма є лінійними підпросторами R3[en], які завжди проходять через початок координат.
У P2 рівняння прямої — і це рівняння може описувати будь-яку пряму на будь-якій площині, паралельній площині при множенні рівняння на .
Якщо , маємо нормалізовані однорідні координати. Усі точки, в яких , утворюють площину. Уявімо, що ми дивимося на цю площину (з точки далі по осі і в напрямку початку координат) і на площині є дві паралельні прямі. З точки огляду ми побачимо тільки частину площини (що обумовлено властивостями зору), яку на малюнку виділено червоним. Якщо ми віддаляємось від площини вздовж осі (продовжуючи дивитися в бік початку координат), ми можемо бачити більшу частину площини. Початкові точки нашого фрагмента огляду пересуваються. Ми можемо відобразити цей рух діленням однорідних координат на константу. На малюнку ми поділили на 2, тому значення тепер стало 0,5. Якщо ми відсуваємося досить далеко, розглянута область перетворюється на точку. В міру віддалення ми бачимо прямі дедалі ширше, при цьому паралельні прямі перетинаються на нескінченно віддаленій прямій (прямій, що проходить через початок координат на площині ). Прямі на площині є ідеальними точками. Площина є нескінченно віддаленою прямою.
Точка з однорідними координатами (0, 0, 0) — це точка, куди сходяться всі дійсні точки, коли ви дивитеся на площину з нескінченності, а пряма на площині ) — це пряма, де перетинаються всі паралельні прямі.

У рівнянні є два вектор-стовпці. При збереженні сталим одного стовпця можна змінювати інший. Якщо зберігати сталою точку x і змінювати коефіцієнти g, отримаємо нові прямі через точку. Якщо ж зберігати сталими коефіцієнти і змінювати точки, які відповідають рівнянню, отримаємо пряму. Ми розглядаємо x як точку, оскільки використовуємо осі , та . Якщо замість цього використати як коефіцієнти осі , , , точки стають прямими, а прямі — точками. Якщо деякий факт доводиться для графічного подання даних[en] при осях , і , ті ж самі доводи можна використовувати для осей , , . Це називають двоїстістю.
Рівняння обчислює скалярний добуток двох вектор-стовпців. Скалярний добуток двох векторів дорівнює нулю, якщо вектори ортогональні. У площині P2 пряму між точками x1 і x2 можна подати як вектор-стовпець g, що задовольняє рівнянням і , або, іншими словами, вектор-стовпець g, ортогональний векторам x1 і x2. Векторний добуток знаходить такий вектор — пряма, що з'єднує дві точки, має однорідні координати, задавані рівнянням . Перетин двох прямих можна знайти в такий самий спосіб, скориставшись двоїістістю, як векторний добуток векторів, що представляють прямі .
Проєктивна площина вкладається в 4-вимірний евклідів простір. Дійсна проєктивна площина P2(R) є фактор-простором 2-сфери
за антиподальним відношенням . Розглянемо функцію задану як . Це відображення обмежується до відображення, областю визначення якого є S2 і, оскільки кожен член є однорідним поліномом парного степеня, воно набуває однакових значень у R4 на кожній з двох антиподальних точок сфери S2. Це дає відображення . Понад те, це відображення є вкладенням. Зауважимо, що це вкладення дозволяє проєкцію в R3, яка є римською поверхнею[en].
Склеївши проєктивні площини одну за одною, отримаємо неорієнтовані поверхні вищого напівроду. Процес склеювання полягає у вирізуванні маленького диска з кожної поверхні та ототожнення (склеювання) меж. Склеювання двох проєктивних площин дає пляшку Кляйна.
Стаття про фундаментальний многокутник[en] описує неорієнтовані поверхні вищого напівроду.
- ↑ а б Apéry, 1987.
- ↑ Weeks, 2002, с. 59.
- ↑ Brehm, 1990, с. 51—56.
- ↑ Richter.
- Apéry F. Models of the real projective plane. — Vieweg, 1987. — ISBN 9783528089559.
- Coxeter H.S.M. The Real Projective Plane. — 2nd ed. — Cambridge: At the University Press, 1955.
- Reinhold Baer. Linear Algebra and Projective Geometry. — Dover, 2005. — ISBN 0-486-44565-8.
- David A. Richter. Two Models of the Real Projective Plane. Процитовано 2010-04-15.
- Weeks J. The shape of space. — Marcel Dekker, Ine, 2002. — (MONOGRAPHS AND TEXTBOOKS IN Pure and Applied Mathematics) — ISBN 0-8247-0709-5.
- Brehm U. How to build minimal polyhedral models of the Boy surface // The mathematical intelligencer. — 1990. — Т. 12, вип. 4.
- Weisstein, Eric W. Дійсна проєктивна площина(англ.) на сайті Wolfram MathWorld.
- Line field coloring using Werner Boy's real projective plane immersion
- Дійсна проєктивна площина на YouTube

















![{\displaystyle [x:y:z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/824605c6ea4c4537ff9daf4ce86c26ef6a30f529)
![{\displaystyle [tx:ty:tz]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01f9d820f27d483153e7e4b0e3ebb3d30fd5e9ae)

![{\displaystyle [x:y:1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbe64dd8a78cef6f5eedea52e24b8452635ea8f9)
![{\displaystyle [x:y:0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f368976b6d23da507c1475db79bbf79887eaa9fc)
![{\displaystyle [0:0:0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04de7716a91f28caabdb519e0600751764a66624)

































