Поле Хіггса
Поле Хі́ггса (англ. Higgs Field; також поширені назви поле Гіґґса, поле Гіггза) — поле, що забезпечує спонтанне порушення симетрії електрослабких взаємодій завдяки порушенню симетрії вакууму, назване на честь розробника його теорії, британського вченого, фізика — теоретика Пітера Хіггса. Квант поля — частинка Хіггса (бозон Хіггса).

На відміну від більшості елементарних полів природи, поле Хіггса має ненульове[1] вакуумне очікуване значення 246 ГеВ. За рахунок цієї особливості, багато частинок, таких як електрон, кварки, бозони слабкої взаємодії W та Z, через взаємодію з полем Хіггса набувають масу[2]. Процес надання маси частинці відомий як механізм Хіггса[3]. Ненульове середнє значення поля Хіггса не є сукупністю відповідних елементарних частинок, оскільки бозон Хіггса є пульсацією поля Хіггса найменш можливої інтенсивності. Пульсація, яка змінюється в просторі і часі, як будь-яка хвиля, а ненульове значення поля залишається незмінним у просторі і часі. Маса бозона Хіггса не повністю походить від поля Хіггса[4]. Не всі частинки отримують масу від взаємодії з полем Хіггса[5]. Дослідження властивостей бозона Хіггса у ЦЕРН продовжується[6] з метою краще зрозуміти саме поле.
Зважаючи на те, що відкриття бозона Хіггса в 2012 році заповнило одну з прогалин Стандартної моделі, виникало закономірне питання — чи в рівняннях, що вивчають фізики, просліджується математичний зв'язок між гравітацією та полем Хіггса. Відповідь на це питання — ні[4]. Оскільки гравітаційні поля мають спін 2 та описуються як частина простору-часу, що взаємодіє з усіма частинками та полями в природі, а поле Хіггса має спін 0, і взаємодіє безпосередньо з елементарними частинками і полями, які також беруть участь в електромагнітній та слабкій ядерній силах.
У стандартній моделі, поле Хіггса є SU(2) дуплетом з двома комплексними скалярними полями з :
Разом вони складають ізоспіновий дуплет () і є носіями гіперзаряду . Самовзаємодія поля Хіггса є причиною спонтанного порушення симетрії , що надає масу калібрувальним бозонам, а також ферміонам. Початковий лагранжіан до змішування і спонтанного порушення симетрії визначається як:
- ,
де
Перші три доданки лагранжіана відповідають за калібрувальну частину, а останні три — за хіггсівську. є самовзаємодіючим потенцілом поля Хіггса. Весь вираз лагранжіана задовольняє калібрувальну симетрію. Останній доданок лагранжіана, відомий як взаємодія Юкави, було додано, щоб згенерувати масу ферміонів. Його можна переписати як:
U(1) заряд поля Хіггса дорівнює 1. Це означає, що поле перетворюється як спінор при SU(2). При U(1) обертаннях, воно множиться на фазу, що змішує дійсні та уявні частини комплексних спінорів один з одним, таким чином, що це не те ж саме, як змішання двох комплексних спінорів при U(1) (який мав би вісім дійсних компонентів), а навпаки є спінорним представленням групи U(2).
Поле Хіггса, через зазначені взаємодії за допомогою свого потенціалу індукує спонтанне порушення трьох з чотирьох генераторів («напрямків») калібрувальної групи SU(2)×U(1): три з чотирьох його компонентів зазвичай складатимуть бозони Ґолдстоуна, якщо вони не були пов'язані з калібрувальними полями.
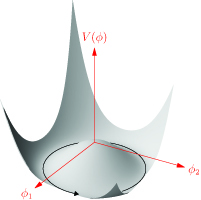
В електрослабкій теорії, різниця між фізичними масами бозонів створюється спонтанним порушенням симетрії поля Хіггса .
Потенціальна енергія поля Хіггса:
- , де
Поле Хіггса є скалярним полем у вакуумі, і його потенціал є симетричним при обертаннях у просторі .
Хіггсів потенціал має форму сомбреро. Мінімум хіггсового потенціалу, відомий як вакуумне очікуване значення, набуває значення
- ГеВ.

Флуктуації навколо мінімуму :
Скалярне поле описує фізичний бозон Хіггса.
Розкладаючи хіггсівський потенціал до другого порядку по :
Додатковий доданок з надає масу бозону Хіггса:

Каплінги вакуумного поля Хіггса з електрослабкими бозонами:
У термінах фізичних бозонів та це дає:
Тобто складові вектора мас бозонів мають вигляд:

Докладніше: Механізм Хіггса
Сильні, слабкі та електромагнітні сили можна зрозуміти як наслідок калібрувальних симетрій. Механізм Хіггса, спонтанне порушення калібрувальних симетрії, є важливим компонентом у розумінні походження мас частинок у Стандартній моделі фізики елементарних частинок. Одним з наслідків відмінності між справжньою симетрією і калібрувальною симетрією, є те, що спонтанне порушення калібрувальної симетрії не приводить до характерних безмасових мод Намбу-Ґолдстоуна (так звані бозони Намбу-Ґолдстоун або просто Ґолдстоун), а приводить тільки до мод, таких як мода Хіггса, що спостерігається в фізиці елементарних частинок.
У Стандартній моделі фізики елементарних частинок, спонтанне порушення симетрії SU(2)×U(1), калібрувальної симетрії, пов'язаної з електрослабкою силою, породжує масу декількох частинок, і відокремлює електромагнітні і слабкі сили. W- і Z-бозони є елементарними частинками, носіями слабкої взаємодії, тоді як фотон є посередником електромагнітної взаємодії. При енергіях значно більших ніж 100 ГеВ всі ці частинки поводяться аналогічним чином. Теорія Вайнберга-Салама передбачає, що при нижчих енергіях ця симетрія порушується таким чином, що виникають фотон і масивні W- і Z- бозони.
Без спонтанного порушення симетрії Стандартна модель взаємодії елементарних частинок вимагає наявності ряду частинок. Однак, деякі частинки (наприклад, W- і Z-бозони) мали б бути безмасовими, коли, насправді, спостереження свідчать, що вони мають масу. Щоб подолати це, спонтанне порушення симетрії доповнюється механізмом Хіггса, щоб забезпечити ці частинки масою. Механізм також передбачав наявність нової частинки, бозона Хіггса, яка успішно була виявлена в 2012 році.
Електрослабка теорія, яка об'єднує електромагнітні та слабкі взаємодії елементарних частинок, починаючи з 1970 року, отримала експериментальну підтримку, безпрецедентну в історії науки[7]. Це об'єднання передбачало тісний зв'язок між безмасовим фотоном, який є носієм дальньодійної електромагнітої сили, та W- і Z- бозонами, які є носіями близькодіючої слабкої сили, а отже повинні бути дуже масивними. До винаходу механізму Хіггса не було відомо, як сформулювати послідовну релятивістську теорії поля з локальною симетрією, яка могла б містити як безмасові носії сили, так і масивні.
У 1962 році в теоремі Ґолдстоуна було показано, що спонтанне порушення симетрії в релятивістської теорії поля спричинює появу безмасових бозонів з нульовим спіном, існування яких було виключене експериментально. У статті, опублікованій в Physics Letters 15 вересня 1964 року, Пітер Хіггс показав, що бозони Ґолдстоуна не повинні виникати, коли спонтанно порушена локальна симетрія в релятивістської теорії. Замість цього, мода Ґолдстоуна забезпечує третю поляризацію масивного векторного поля. Інша мода вихідного скалярного дуплета залишається як масивна бесспінова частинка — бозон Хіггса.
Хіггс написав другу коротку статтю, що описувала модель, яка пізніше отримала назву «механізм Хіггса», та представив цю статтю Physics Letters, але її відхилили на підставі того, що вона не заслуговує швидкої публікації. Хіггс доопрацював статтю і представив її журналу Physical Review Letters, де вона була прийнята, але рецензент, яким виявився Йотіро Намбу, попросив Хіггса прокоментувати відношення його роботи до роботи Франсуа Енглерта та Браута, яка була опублікована в Physical Review Letters 31 серпня 1964 року, того ж дня, коли було отримано статтю Хіггса. Хіггс не знав про роботу брюссельської групи, оскільки її препринт не був надісланий до Единбурга. Переглянувши документ, Хіггс звернув увагу на можливість масивного безспінового бозона, наведену в останньому абзаці статті брюссельської групи. У жовтні 1964 року Хіггс провів переговори з Джеральдом Гуральником, Карлом Хагеном та Томом Кібблом, який виявив яким чином маси невзаємодіючих векторних бозонів можуть бути отримані за допомогою механізму Андерсона.
Як Енглерт і Браут, Хіггс не уточнював скалярний потенціал і називав його , але передбачав його таким, що симетрія спонтанно порушується вакуумним очікуваним значенням . Потім він вивчав рівняння руху для малих коливань навколо цього вакууму і ввів нову змінну
де використав калібрувальне перетворення, щоб поглинути моду Намбу-Ґолдстоуна . Завдяки цьому він зміг переписати рівняння руху у вигляді
яке він правильно інтерпретував як калібрувальне інваріантне рівняння руху для масивного вектора частинок. Аналіз було проведено на лінійному рівні, але було очевидно, що рівняння можна доповнити нелінійними членами. Потім Хіггс зауважив, що залишкове скалярне поле задовольняє наступне рівняння руху
яке показує чисту масу залишкової скалярної частинки. Той факт, що Хіггс отримав явний вираз для чистої маси скалярної частинки і привело до назви «частинка Хіггса», хоча ця частинка також є наслідком механізму Енглерта-Браута.
За рік до цього Філіп Андерсон зазначив, що, в надпровіднику, де локальна калібрувальна симетрія спонтанно порушена, мода Ґолдстоуна стає масивною за рахунок взаємодії з калібрувальним полем, в той час як електромагнітні режими масивні (ефект Мейснера), незважаючи на калібрувальну інваріантність. Проте, він не обговорював жодної релятивістської моделі і оскільки інваріантність Лоренца є найважливішим компонентом теореми Ґолдстоуна, він не продемонстрував, що проблему можна обійти. У другій статті 1964 Хіггс послався на роботу Андерсона таким чином, що малось на увазі, ніби Андерсон знав про нерелятивістський аналог хіггсівського бозона. Насправді, Андерсон не знав, і так було до 1981 року, коли несподівана особливість спектру комбінаційного розсіювання NbSe2 була пояснена через «масивну колективну моду, що існує у всіх надпровідниках — коливання амплітуди надпровідної щілини».
Пошуки бозона Хіггса стали однією з основних задач експериментальної фізики елементарних частинок. Незважаючи на те, що його маса за електрослабкими розрахунками прогнозувалась у межах від 52 до 110 ГеВ, значення нижче 114 ГеВ було виключено. Його маса не могла перевищувати 1 ТеВ, за умови, що електрослабка теорія залишаєтися в силі на таких масштабах енергії, а саме в діапазоні, який знаходиться в межах досяжності Великого адронного колайдера в ЦЕРНі. Експериментальні групи ATLAS і CMS в ЦЕРН виявили хіггсівський бозон з масою близько 126 ГеВ, що узгоджується з властивостями Стандартної моделі.
- John F. Gunion, The Higgs Hunter's Guide. — Westview Press, 2008. — 256 p.
- Yorikiyo Nagashima, Elementary Particle Physics: Quantum Field Theory and Particles, v1. — Wiley-VHC, 2013. — 646p.
- Sean Carrol, The Particle at the End of the Universe. — Dutton, 2012. — 352p.






![{\displaystyle {\mathfrak {L}}_{EW}={\bar {\Psi }}\imath \gamma ^{\mu }D_{\mu }\Psi -{\frac {1}{4}}F_{\mu v}F^{\mu v}-{\frac {1}{4}}B_{\mu v}B^{\mu v}+(D_{\mu }\Phi )^{\dagger }(D^{\mu }\Phi )-V(\Phi )-G_{f}\left[{\bar {e_{R}}}(\Phi ^{\dagger }\Psi _{L})+({\bar {\Psi }}_{L}\Phi )e_{R}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70abe5ef76392c488f6c0c276aae79419614692e)


































