Просторове передбачувальне моделювання
Просторове передбачувальне моделювання (Geospatial predictive modeling) — загалом це будь-який метод передбачення, який включає в себе просторову залежність. Просторовий аналіз заснований на географічному розташуванні і взаємозв'язках спостережуваних даних. Просторовий аналіз дозволяє зрозуміти структуру специфічної діяльності у просторі. Геопросторове передбачувальне моделювання намагається описати ті обмеження і впливи через просторово корелюючі випадки історичних геопросторових місць розташування із чинниками зовнішнього середовища, які представляють ці обмеження і впливи. Просторове передбачувальне моделювання — процес аналізу подій через географічний фільтр для того, щоб знайти ймовірності настання подій або непередбачуваних випадків[1].
Вперше просторове передбачення було розвинене геостатистикою, що напряму пов'язано із гірничою промисловістю в ранніх 50-их. Починаючи з цього періоду, швидкісні та недорогі обчислювальні методи зробили легким дослідження даних, що раніше було дуже важким. Одна із галузей, що отримала надзвичайну вигоду з цієї нової свободи, — це непараметрична статистика. Проте, хоча більшість з існуючих теоретичних непараметричних результатів залежних випадкових змінних відносяться до вказаних часових (динамічних) рядів, де односпрямований потік часу лежить в основі конструкції моделей, доступні лише порівняно декілька узагальнень до просторової області[2].
Існують два загальнонаукові типи просторових передбачувальних моделей: дедуктивна та індуктивна.
Дедуктивний метод ґрунтується на якісних даних або даних експерта з певного предмету (SME), щоб описати взаємозалежність між настанням події і факторами, які описують середовище. В результаті, дедуктивний процес загалом покладається на більш суб'єктивну інформацію. Дослідник може потенційно обмежувати модель тільки введенням ряду факторів, які може осягнути людський мозок. Нижче зазначено приклад дедуктивної моделі: Множина подій зазвичай знаходять .
- Між 100 і 700 метрів від аеропортів.
- У рослинному покрові галявини.
- У висоті між 1000 і 1500 метрами.
У цій дедуктивній моделі, на високу придатність місця для множини подій впливають неемпірично визначені межі пресування в просторі для аеропортів, рослинних покровів і висот: скрізь в інших місцях знаходяться області нижчої придатності. Точність і деталі дедуктивної моделі обмежуються глибиною якісних вхідних даних моделі.
Індуктивний метод ґрунтується на емпірично визначеній просторовій залежності між історичними або відомими місцями настання події і факторами, які складають середовище (інфраструктурні, соціокультурні, топографічні та інші). Кожен випадок події вноситься у план в географічному просторі і кількісні стосунки визначаються між випадком події і чинниками, які визначають вплив довкілля. Перевага цього методу у тому, що програмне забезпечення може розвиватися, щоб досвідченим шляхом виявити — використовуючи швидкість комп'ютерів, яка критична, коли сотні чинників включені, — як відомі, так і невідомі кореляції між чинниками і подіями. Ті кількісні зв'язки значень потім обробляє статистична функція, щоб знайти просторові моделі, які визначають високо- і низькопридатні для настання події області[3].
Доволі простим і популярним методои просторового передбачення є звичайний кригінг. Простий крижєинг потребує моделі просторової послідовності, або залежності. Частіше за все він представлений у формі коваріації або семіваріограми.
За цим підходом просторове передбачення може бути представлене за допомогою програмного забезпечення SAS/STAT, за наступною послідовністю кроків. Спершу, необхідно змоделювати коваріацію або семіваріограму просторового процесу, користуючись процедурою VARIOGRAM. Це включає вибір як математичної форми, так і значень зв'язаних параметрів. По-друге, користуючись цією моделлю залежності пояснити систему криджингу у вказаному наборі просторових пунктів, що є у результаті дає прогнозовані значення і пов'язані стандартні похибки. Процедура KRIGE2D виконує другий з цих кроків, використовуючи звичайний криджинг двовимірних даних.
Процедура VARIOGRAM обчислює зразокові або емпіричні виміри просторової послідовності для двовимірних просторових даних. Вимірами послідовності є нормальна семіваріограма, більш груба версія семіваріограми і коваріація. Виміри послідовності записуються вихідному наборі даних, дозволяючи будувати графіки і проводити оцінку параметрів для теоретичної семіваріограми або моделі коваріації. Можливе використання обох вимірів як ізотропічного, так і анізотропні.
Процедура KRIGE2D виконує звичайний криджинг в двох вимірах. PROC KRIGE2D може управляти анізотропними і вкладеними моделями семіваріограм. Чотири моделі семіваріограм підтримуються: моделі Гауса, експоненціальні (показової функції), сферичні і степеневі моделі.
Локальний криджинг підтримується через специфікацію радіусу навколо певної координати або специфікацію ряду найближчих сусідів для використання в системі криджингу. Коли ви виконуєте локальний криджинг, окрема криджингова система вирішується в кожній координаті, користуючись близькістю точок даних, що встановлюється радіусом або числом деталізації. Ви можете точно визначити розташування криджингових оцінок в звіті GRID (інтерактивний графічний дисплей), або вони можуть бути взяті з SAS масиву даних. Сіткова деталізація найкраще відповідає регулярній сітці; специфікація масиву даних може управляти будь-якою неправильною моделлю точок[4].
Добування просторових знань є похідною від виявлення експертних знань в базах даних (Knowledge Discovery — KDD). Просторові відомості зберігаються в географічних інформаційних системах (GIS), які є базами даних з додатковою функціональністю для виконання просторових маніпуляцій і запитів даних. Добування просторових знань об'єднує методи інтелектуального аналізу даних і GIS для формування багатовимірного аналізу, результати якого потім проектується на двовимірний географічні зображення. Ця взаємодія є важливою, оскільки дозволяє результати складного багатовимірного аналізу представляти в інтуїтивно зрозумілій формі для користувача.
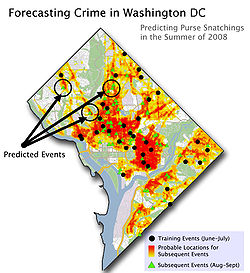
Просторовим прогнозом також називають один із напрямків передбачувального аналізу злочинів. Це включає перегляд попередніх місць де відбувалися злочини, і користуючись цією інформацією, передбачення місця розташування або області наступного удару в серії. В основному, аналітик намагається ідентифікувати простір компетентності злочинця. Після того, як на основі певної просторової статистики створена модель просторової компетентності злочинця, в межах цього простору усвідомлення ідентифікуються певні цілі або мішені, це дає змогу поліції встановити спостереження з метою затримання злочинця в процесі вчинення злочину. Хоча ця техніка не набула такого розголосу як, наприклад, географічне профілювання, але ймовірно вона є більш плідною у багатьох поліцейських відділах по всій країні. Проте, її в жодному разі не можна назвати досконалою. Ця техніка використовує важкі для передбачення людські рішення, але було доведено, що вони все одно мають певну надійну ймовірність передбачення. Коли ця техніка успішна, це — вигідно як для забезпечення правопорядку, так і для громадян міста, оскільки це профілактичний захід, а не реактивний. Охорона правопорядку, що зазвичай є реактивною за своєю природою, отримує більшу вигоду, коли бере на себе профілактичну роль. «Уважний предикативний аналіз злочинів має зробити можливим скорочення міського рівня злочинності завдяки правильнішому розподілу ресурсів правосуддя і гнучкішим рішенням у міському плануванні» (Родос і Conly, 1981)[5].
Методика попередження терористичних актів ґрунтується на попередній роботі в прогнозуванні злочинної поведінки з використанням просторових моделей вибору. Для цього прогнозу використовується поєднання двох методів моделювання просторового вибору терористами-смертниками в єдиний прогноз, який поєднує просторове моделювання ймовірності характеристик зовнішнього середовища із логістичною регресією моделювання демографічних чинників[6].
Більшість просторових методів прогнозування використовують тільки минулі місця для прогнозування майбутніх місць (наприклад, кригінг). Модель просторових переваг у багатовимірному просторі формується за відстанню до важливих географічних або ключових чинників. Передбачається, що ці відстані мають розподіл Гауса з середнім значенням нуль (тобто терорист віддає перевагу розміщувати напад на певній відстані від цих місць). Шляхом вимірювання відстаней від настання випадку до ключових чинників ми будуємо все більш і більш точне судження щодо терористичних преференцій. Ці чинники є набагато більш наглядними, ніж географічні координати, які є просто індексом векторних даних.
Інший підхід для обчислення ймовірності нападу — логістична регресія. Логістична регресія є рішенням в замкнутій формі для моделювання ймовірностей вибору, причетних до вибору місця терористичної атаки і може пояснити відстань до ключових чинників, а також категоріальні змінні (наприклад, присутність свята). Ймовірність події потім порівнюється з пороговим значенням і приймається класифікаційне рішення. Логістична регресія може включати в себе і інші змінні, не лише відстані, для прогнозування терактів, а саме можуть використовуватися і демографічні атрибути. Далі кожному посиланню на комірку сітки дається оцінка від 0 до 1, яка представляє ймовірність того, що подія відбудеться. Ця сітка затемнюється згідно з близькими значеннями, як для відображення моделі просторової ймовірності.
Оскільки просторові моделі не є незалежними, ми не можемо по'єднати дві ймовірності, як би ми робили із двома незалежними показниками. Замість цього ми використовуємо демографічні дані для доповнення або віднімання від просторової моделі відповідно до її власної оцінки. Через те, що демографічна модель за своєю суттю розбивається на складові частини відповідно до границь поєднаної сукупності, це злиття має ефект «механічної пили» просторові моделі та переміщює області до більш високих або низьких оцінок. Відірвані області, які з'являються, на перспективному зображенні, є областями, які були зрушені в зв'язку з злиттям моделей.
- ↑ Colonel Jonathan, Samuel Huddleston. Mathematical Literacy as a Fundamental Component of Training Cyber Warriors: Moving Beyonf the Tools and Towards Fishing. Cyberspace Symposium II, Combined Arms Center, Fort Leavenworth, Kansas. — The Nexus, october 2008 Edition, vol.1/1.
- ↑ BLAU Gerard, CADRE Benoit. Nonparametric Spatial Prediction.
- ↑ Gary P. Beauvais, Douglas A. Keinath, Pilar Hernandez, Larry Master, Rob Thurston. Element Distribution Modeling: A Primer (Version 2), Natureserve, Arlington, Virginia, June 1, 2006
- ↑ Knowledge Base of SAS software. — http://support.sas.com/rnd/app/da/new/daspat.html [Архівовано 15 червня 2012 у Wayback Machine.]
- ↑ John B. Van Auken. An evaluation of spatial forecasting technoques used in tactical crime analysis, April 2005
- ↑ Donald Brown, Jason Dalton, and Heidi Hoyle. Spatial forecast methods for terrorist events in urban environments, In Proceedings of the Second NSF/NIJ Symposium on Intelligence and Security Informatics, Lecture Notes in Computer Science, pages 426—435, Tucson, Arizona, Springer-Verlag Heidelberg, June 2004
На цю статтю не посилаються інші статті Вікіпедії. Будь ласка розставте посилання відповідно до прийнятих рекомендацій. |
