Рекурентна нейронна мережа
| Частина з циклу |
| Машинне навчання та добування даних |
|---|
 |
Рекуре́нтні нейро́нні мере́жі (РНМ, англ. recurrent neural networks, RNN) — це клас штучних нейронних мереж, у якому з'єднання між вузлами утворюють граф орієнтований у часі. Це створює внутрішній стан мережі, що дозволяє їй проявляти динамічну поведінку в часі. На відміну від нейронних мереж прямого поширення, РНМ можуть використовувати свою внутрішню пам'ять для обробки довільних послідовностей входів. Це робить їх застосовними до таких задач, як розпізнавання несегментованого неперервного рукописного тексту[1] та розпізнавання мовлення.[2]
Це — основна архітектура, розроблена в 1980-х роках: мережа нейроноподібних вузлів, кожен з орієнтованим з'єднанням до кожного іншого вузла.[джерело?] Кожен з вузлів має змінну в часі дійснозначну активацію. Кожне з'єднання має змінювану дійснозначну вагу[en]. Деякі з вузлів називаються входовими вузлами, деякі — виходовими, а решта — прихованими вузлами. Більшість із наведених нижче архітектур є окремими випадками.
Для постановок керованого навчання з дискретним часом тренувальні послідовності входових векторів стають послідовностями активацій входових вузлів, по одному вектору на кожен момент часу.[прояснити] В кожен заданий момент часу кожен не входовий вузол обчислює свою поточну активацію як нелінійну функцію від зваженої суми активацій всіх вузлів, від яких до нього надходять з'єднання.[прояснити] Для деяких із виходових вузлів на певних тактах можуть бути задані вчителем цільові активації. Наприклад, якщо входова послідовність є мовленнєвим сигналом, що відповідає вимовленій цифрі, то кінцевий цільовий вихід у кінці послідовності може бути міткою, яка класифікує цю цифру. Для кожної послідовності її похибка є сумою відхилень усіх цільових сигналів від відповідних активацій, обчислених мережею. Для тренувального набору численних послідовностей загальна похибка є сумою похибок усіх окремих послідовностей. Алгоритми мінімізації цієї похибки згадано в розділі алгоритмів тренування нижче.
У постановках навчання з підкріпленням не існує вчителя, який надавав би цільові сигнали для РНМ, натомість час від часу застосовується функція допасованості або функція винагороди для оцінювання продуктивності РНМ, яка впливає на її входовий потік через виходові вузли, з'єднані з приводами, що впливають на середовище. Знов-таки, зробіть порівняння в розділі про тренувальні алгоритми нижче.
Рекурсивна нейронна мережа[3] створюється рекурсивним застосуванням одного й того ж набору ваг до диференційовної графоподібної структури шляхом обходу цієї структури в топологічній послідовності. Також, такі мережі зазвичай тренують зворотним режимом автоматичного диференціювання.[4][5] Їх було введено для навчання розподілених представлень структури, таких як терміни логіки. Окремим випадком рекурсивних нейронних мереж є самі РНМ, чия структура відповідає лінійному ланцюжкові. Рекурсивні нейронні мережі застосовували до обробки природної мови.[6] Рекурсивна нейронна тензорна мережа (англ. Recursive Neural Tensor Network) використовує функцію компонування на основі тензорів для всіх вузлів дерева.[7]
Мережа Хопфілда становить історичний інтерес, хоч вона й не є загальноприйнятою РНМ, оскільки її побудовано не для обробки послідовностей зразків. Вона натомість вимагає стаціонарних входів. Вона є РНМ, в якій усі з'єднання є симетричними. Винайдена Джоном Хопфілдом 1982 року, вона гарантує, що її динаміка збігатиметься. Якщо з'єднання тренуються із застосуванням геббового навчання, то мережа Хопфілда може працювати як робастна асоціативна пам'ять, стійка до змін з'єднань.
Одним із варіантів мережі Хопфілда є двоспрямована асоціативна пам'ять (ДАП, англ. bidirectional associative memory, BAM). ДАП має два шари, кожен з яких можна використовувати як входовий, щоби викликати асоціацію й виробити вихід на іншому шарі.[8]
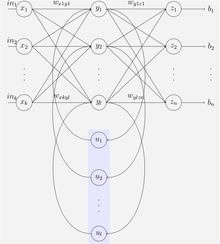
Наступний окремий випадок наведеної вище основної архітектури було застосовано Джеффом Елманом[en]. Використовується тришарова мережа (впорядкована на ілюстрації по горизонталі як x, y та z) з додаванням набору «контекстних вузлів» (англ. context units, на ілюстрації — u). Існують з'єднання з середнього (прихованого) шару з цими контекстними вузлами з незмінними одиничними вагами.[9] На кожному такті вхід поширюється стандартним прямим чином, а потім застосовується правило навчання. Незмінні зворотні з'єднання призводять до того, що контекстні вузли завжди зберігають копію попередніх значень прихованих вузлів (оскільки вони поширюються з'єднаннями до застосування правила навчання). Таким чином, мережа Елмана може зберігати свого роду стан, що дозволяє їй виконувати такі задачі, як передбачення послідовностей, що є за межами можливостей стандартного багатошарового перцептрону.
Мережі Джордана, що завдячують своєю назвою Майклові І. Джордану[en], подібні до мереж Елмана. Проте подавання на контекстні вузли йде з виходового шару замість прихованого. Контекстні вузли в мережі Джордана також називають шаром стану, і вони мають рекурентні з'єднання самі з собою, без інших вузлів на цих з'єднаннях.[9]
Мережі Елмана та Джордана відомі також як «прості рекурентні мережі» (ПРМ, англ. simple recurrent networks, SRN).
Змінні та функції
- : входовий вектор
- : вектор прихованого шару
- : виходовий вектор
- , та : матриці та вектор параметрів
- та : функції активації
Резервуарне обчислення — особливий підхід у рекурентних нейронних мережах, що використовує фіксовану випадкову структуру, відому як «резервуар», для ефективної обробки тимчасових даних. Резервуар складається з взаємопов'язаних вузлів із випадковими з'єднаннями, що утворюють динамічну систему, здатну вловлювати складні часові закономірності. На відміну від традиційних РНМ, обчислення пластів передбачає навчання лише вихідного рівня, що спрощує процес навчання. Його обчислювальна ефективність, яка пояснюється фіксованою структурою резервуару, робить його вигідним для завдань, що потребують інтенсивної пам'яті. Застосування охоплюють різні сфери, такі як прогнозування часових рядів і розпізнавання мовлення, демонструючи свою ефективність у обробці послідовних даних. Типи, такі як мережа з відлунням стану (Echo State Networks) і рідкий скінченний автомат (Liquid State Machines,) розширюють його застосування в різних контекстах.[12][13]
Незважаючи на свої переваги, оптимізація продуктивності пласта для конкретних завдань залишається проблемою. Тим не менш, резервуарні обчислення є перспективною архітектурою в РНМ, пропонуючи обчислювальну ефективність і майстерність в обробці тимчасової інформації. Постійні дослідження спрямовані на підвищення його можливостей і розширення його застосування в різних сферах. Ця парадигма являє собою значний прогрес в архітектурі нейронних мереж, готовий запровадити інновації в часовій обробці даних.[12][13]
Мережа з відлунням стану (англ. echo state network, ESN) — це рекурентна нейронна мережа з розріджено з'єднаним випадковим прихованим шаром. Унікальність цієї мережі полягає у тому, що лише ваги виходних нейронів підлягають змінам та навчанню, тоді як структура та внутрішній стан резервуару залишаються незмінними. Такі мережі є добрими для відтворення певних часових рядів.[14]
Основні особливості[15][12][16]:
- Резервуар у мережі з відлунням стану має велику кількість взаємопов'язаних вузлів, що формують розріджений прихований шар.
- Лише вихідні ваги піддаються тренуванню, що спрощує процес навчання та зменшує обчислювальну складність.
- Мережі з відлунням стану відомі своєю здатністю успішно відтворювати складні часові ряди та використовуються у завданнях прогнозування та моделювання послідовних даних.
Варіант для нейронів з потенціалом дії[en] відомий як рідкі скінченні автомати.[17] Ця модифікація мережі дозволяє здійснювати більш точні та гнучкі прогнози в обробці послідовних даних.[18][19][20][21]
Проблему зникання градієнту[22] автоматичного диференціювання та зворотного поширення в нейронних мережах було частково подолано 1992 року ранньою породжувальною моделлю, названою нейронним стискачем історії, реалізованою як некерована стопка рекурентних нейронних мереж (РНМ).[23] РНМ на входовому рівні навчається передбачувати свій наступний вхід з історії попередніх входів. Лише непередбачувані входи певної РНМ в цій ієрархії стають входами до РНМ наступного вищого рівня, яка відтак переобчислює свій внутрішній стан лише зрідка. Кожна РНМ вищого рівня відтак навчається стисненого представлення інформації в нижчій РНМ. Це здійснюється таким чином, що вхідну послідовність може бути точно відтворено з представлення цієї послідовності на найвищому рівні. Ця система дієво мінімізує довжину опису або від'ємний логарифм імовірності даних.[24] Якщо в послідовності вхідних даних є багато передбачуваності, яка піддається навчанню, то РНМ найвищого рівня може використовувати кероване навчання, щоби легко класифікувати навіть глибокі послідовності з дуже тривалими часовими інтервалами між важливими подіями. 1993 року така система вже розв'язала задачу «дуже глибокого навчання» (англ. Very Deep Learning), яка вимагає понад 1 000 послідовних шарів в розгорнутій у часі РНМ.[25]
Також можливо перегнати всю цю ієрархію РНМ в лише дві РНМ, що називають «свідомим» фрагментатором (англ. "conscious" chunker, вищий рівень) та «підсвідомим» автоматизатором (англ. "subconscious" automatizer, нижчий рівень).[23] Щойно фрагментатор навчився передбачувати та стискати входи, які є все ще не передбачуваними автоматизатором, то в наступній фазі навчання можна навантажити автоматизатор передбачуванням або імітуванням через особливі додаткові вузли прихованих вузлів повільніше змінюваного фрагментатора. Це полегшує автоматизаторові навчання доречних рідко змінюваних спогадів протягом дуже тривалих проміжків часу. Це, своєю чергою, допомагає автоматизаторові робити багато з його колись непередбачуваних входів передбачуваними, таким чином, що фрагментатор може зосередитися на решті все ще непередбачуваних подій, щоби стискати дані ще сильніше.[23]
Численні дослідники нині використовують РНМ глибокого навчання, яку називають мережею довгої короткочасної пам'яті (ДКЧП, англ. long short-term memory, LSTM), опубліковану Хохрайтером[en] та Шмідгубером 1997 року.[26] Це система глибокого навчання, яка, на відміну від традиційних РНМ, не має проблеми зникання градієнту (порівняйте в розділі алгоритмів тренування нижче). ДКЧП в нормі є доповненою рекурентними вентилями, які називають забувальними (англ. forget gates).[27] РНМ ДКЧП запобігають зниканню та вибуханню зворотно поширюваних похибок.[22] Натомість похибки можуть плинути в зворотному напрямку крізь необмежене число віртуальних шарів розгорнутої в просторі РНМ ДКЧП. Тобто, ДКЧП може вчитися завдань «дуже глибокого навчання» (англ. Very Deep Learning),[28] які вимагають спогадів про події, що трапилися тисячі або навіть мільйони тактів тому. Можливо розвивати ДКЧП-подібні проблемно-орієнтовані топології.[29] ДКЧП працює навіть за тривалих затримок, і може обробляти сигнали, що мають суміш низько- та високочастотних складових.
Нині багато застосунків використовують стопки РНМ ДКЧП[30] і тренують їх нейромережевою часовою класифікацією (НЧК, англ. Connectionist Temporal Classification, CTC)[31] для знаходження такої вагової матриці РНМ, яка максимізує ймовірність послідовностей міток у тренувальному наборі для заданих відповідних вхідних послідовностей. НЧК досягає як вирівнювання, так і розпізнавання. Близько 2007 року ДКЧП почали революціювати розпізнавання мовлення, перевершуючи традиційні моделі в деяких мовленнєвих застосуваннях.[32] 2009 року ДКЧП, тренована НЧК, стала першою РНМ, яка перемогла в змаганнях із розпізнавання образів, коли вона виграла кілька змагань із неперервного рукописного розпізнавання.[28][33] 2014 року китайський пошуковий гігант Baidu застосував РНМ, треновані НЧК, щоби перевершити еталон розпізнавання мовлення Switchboard Hub5'00, без застосування жодних традиційних методів обробки мовлення.[34] ДКЧП також поліпшила велико-словникове розпізнавання мовлення,[35][36] синтез мовлення з тексту,[37] також і для Google Android,[28][38] і фото-реалістичні голови, що розмовляють.[37] 2015 року в розпізнаванні мовлення Google, як повідомляється, стався різкий 49-відсотковий[джерело?] стрибок продуктивності завдяки НЧК-тренованій ДКЧП, яка тепер доступна через Google Voice Search всім користувачам смартфонів.[39]
ДКЧП також стала дуже популярною в галузі обробки природної мови. На відміну від попередніх моделей на основі ПММ та подібних понять, ДКЧП може вчитися розпізнавати контекстно-чутливі мови[en].[40] ДКЧП поліпшила машинний переклад,[41] моделювання мов[42] та багатомовну обробку мов.[43] ДКЧП у поєднанні зі згортковими нейронними мережами (ЗНМ) також поліпшила автоматичний опис зображень[44] і безліч інших застосувань.
Вентильний рекурентний вузол (англ. gated recurrent unit) є однією з рекурентних нейронних мереж, представлених 2014 року.
Винайдена Шустером та Палівалом 1997 року,[45] двонаправлена РНМ (англ. bi-directional RNN), або ДРНМ (англ. BRNN), використовує скінченну послідовність, щоби передбачувати або мітити кожен елемент цієї послідовності на основі як минулого, так і майбутнього контексту цього елементу. Це здійснюється шляхом з'єднання виходів двох РНМ, одна з яких обробляє послідовність зліва направо, а інша — справа наліво. Поєднані виходи є передбаченнями заданих учителем цільових сигналів. Ця методика виявилася особливо корисною при поєднанні з РНМ ДКЧП.[46]
Рекурентна нейронна мережа неперервного часу (РНМНЧ, англ. continuous time recurrent neural network, CTRNN) — це модель динамічних систем біологічних нейронних мереж. Для моделювання впливів на нейрон входового ланцюжка активацій РНМНЧ застосовує систему звичайних диференціальних рівнянь.
Для нейрону в мережі з потенціалом дії темп зміни збудження задається як
де
- : часова стала постсинаптичного вузла
- : збудження постсинаптичного вузла
- : темп зміни збудження постсинаптичного вузла
- : вага з'єднання від пре- до постсинаптичного вузла
- : сигмоїда , наприклад, .
- : збудження пресинаптичного вузла
- : упередження пресинаптичного вузла
- : вхід (якщо є) до вузла
РНМНЧ часто застосовували в галузі еволюційної робототехніки[en], де їх використовували, щоби братися за, наприклад, бачення,[47] взаємодію[48] та мінімально пізнавальну поведінку.[49]
Зауважте, що за теоремою відліків Шеннона рекурентні нейронні мережі дискретного часу можна розглядати як рекурентні нейронні мережі неперервного часу, в яких диференціальне рівняння було перетворено на рівнозначне різницеве рівняння після того, як функції збудження постсинаптичних вузлів було пропущено через низькочастотний фільтр перед дискретизацією.
Існує багато прикладів ієрархічних РНМ (англ. hierarchical RNN), чиї елементи з'єднано різними способами для розкладу ієрархічної поведінки на корисні підпрограми.[23][50]
Як правило, рекурентний багатошаровий перцептрон (РБШП, англ. Recurrent Multi-Layer Perceptron, RMLP) складається з ряду каскадованих підмереж, кожна з яких складається з декількох шарів вузлів. Кожна з цих підмереж є мережею прямого поширення повністю, крім останнього шару, який може мати зворотні зв'язки всередині себе. Кожна з цих підмереж під'єднується лише зв'язками прямого поширення.[51]
РНМ другого порядку (англ. second order RNN) використовують ваги вищих порядків замість стандартних вагів , а входи та стани можуть бути добутком. Це уможливлює пряме відображення на скінченний автомат, як у тренуванні, стійкості, так і в представленні.[52][53] Довга короткочасна пам'ять є прикладом цього, крім того, що вона не має таких формальних відображень та доведення стійкості.
Модель рекурентної нейронної мережі кількох масштабів часу (англ. multiple timescales recurrent neural network, MTRNN) є можливою обчислювальною моделлю на нейронній основі, яка до деякої міри імітує діяльність головного мозку.[54][55] Вона має здатність імітувати функційну ієрархію головного мозку через самоорганізацію, яка залежить не лише від просторових зв'язків між нейронами, а й від окремих типів нейронної активності, кожного з окремими часовими властивостями. За таких різних нейронних активностей неперервні послідовності будь-якої множини поведінки сегментуються на придатні до повторного використання примітиви, які своєю чергою гнучко вбудовуються до різноманітних послідовностей поведінки. Біологічне підтвердження такого типу ієрархії обговорювалося в теорії пам'яті—передбачування функціювання мозку Джеффом Гокінсом[en] у його книзі «Про інтелект».
англ. Pollack's sequential cascaded networks
Нейронні машини Тюрінга (НМТ, англ. Neural Turing machine, NTM) — це метод розширення можливостей рекурентних нейронних мереж шляхом з'єднання їх із зовнішніми ресурсами пам'яті, з якими вони можуть взаємодіяти за допомогою процесів зосередження уваги. Така об'єднана система аналогічна машині Тюрінга або архітектурі фон Неймана, але є диференційовною з краю в край, що дозволяє їй продуктивно тренуватися за допомогою градієнтного спуску.[56]
Нейромережеві магазинні автомати (англ. Neural network pushdown automata, NNPDA) аналогічні НМТ, але стрічки замінюються аналоговими стеками, які є диференційовними, і тренуються для керування. Таким чином, вони подібні за складністю до розпізнавачів контекстно-вільних граматик.[57]
Представлені вперше Бартом Коско,[58] мережі двоспрямованої асоціативної пам'яті (ДАП, англ. bidirectional associative memory, BAM) зберігають асоціативні дані як вектор. Двоспрямованість походить від передавання інформації матрицею та її транспозицією. Як правило, для двійкового кодування пар асоціацій віддають перевагу біполярному кодуванню[en]. Нещодавно стохастичні моделі ДАП з марковським кроком було оптимізовано для вищої стійкості мережі та відповідності для реальних застосувань.[59]
Щоби мінімізувати загальну похибку, може застосовуватися градієнтний спуск для зміни кожної ваги пропорційно похідній похибки по відношенню до цієї ваги, за умови, що нелінійні функції активації є диференційовними. Для здійснення цього в 1980-х і на початку 1990-х років було розроблено різні методи Полом Вербосом[en], Рональдом Вільямсом, Тоні Робінсоном, Юргеном Шмідгубером, Зеппом Хохрайтером[en], Бараком Перлмуттером та іншими.
Стандартний метод називається «зворотне поширення в часі» (англ. backpropagation through time), або ЗПЧ (англ. BPTT), і є узагальненням зворотного поширення для мереж прямого поширення,[60][61] і, як і той метод, є зразком автоматичного диференціювання в режимі зворотного накопичення, або принципу мінімуму Понтрягіна. Обчислювально більш витратний інтерактивний варіант називається «реальночасове рекурентне навчання» (англ. Real-Time Recurrent Learning), або РЧРН (англ. RTRL),[62][63] і є зразком автоматичного диференціювання в режимі послідовного накопичення зі складеними векторами тангенсів. На відміну від ЗПЧ, цей алгоритм є локальним в часі, але не локальним у просторі.
В цьому контексті локальний у просторі означає, що вектор ваг вузла може бути уточнено лише із застосуванням інформації, що зберігається в з'єднаних вузлах та самому вузлі, так що складність уточнення одного вузла є лінійною по відношенню до розмірності вектору ваг. Локальний в часі означає, що уточнення відбуваються неперервно (інтерактивно), і залежать лише від найнещодавнішого такту, а не від декількох тактів у межах заданого обрію часу, як у ЗПЧ. Біологічні нейронні мережі видаються локальними як у часі, так і в просторі.[64][65]
Недоліком РНРЧ є те, що для рекурсивного обчислення часткових похідних від має часову складність Ο(кількість прихованих × кількість ваг) на такт для обчислення матриць Якобі, тоді як ЗПЧ займає лише Ο(кількість ваг) на такт, ціною, проте, зберігання всіх прямих активацій в межах заданого обрію часу.[66]
Існує також інтерактивний гібрид ЗПЧ і РНРЧ з проміжною складністю,[67][68] і є варіанти для неперервного часу.[69] Головною проблемою градієнтного спуску для стандартних архітектур РНМ є те, що градієнти похибки зникають експоненційно швидко з розміром часової затримки між важливими подіями.[22][70] Як спробу подолання цих проблем було запропоновано архітектуру довгої короткочасної пам'яті разом з гібридним методом навчання ЗПЧ/РНРЧ.[26]
Крім того, інтерактивний алгоритм, що називається причинним рекурсивним зворотним поширенням (ПРЗП, англ. causal recursive backpropagation, CRBP), реалізує та поєднує разом парадигми ЗПЧ та РНРЧ для локальної рекурентної мережі.[71] Він працює з найзагальнішими локально рекурентними мережами. Алгоритм ПРЗП може мінімізувати глобальну похибку; цей факт призводить до поліпшеної стійкості алгоритму, забезпечуючи об'єднавчий погляд на методики градієнтних обчислень для рекурентних мереж із локальним зворотним зв'язком.
Цікавий підхід до обчислення градієнтної інформації в РНМ довільних архітектур, що запропонували Ван та Буфе,[72] ґрунтується на діаграмному виведенні графів плину сигналу для отримання пакетного алгоритму ЗПЧ, тоді як Камполуччі, Унчіні та Піацца запропонували його швидку інтерактивну версію[73] на основі теореми Лі[74] для обчислення чутливості мереж.
Тренування ваг у нейронній мережі можливо моделювати як нелінійну задачу глобальної оптимізації. Цільову функцію для оцінки допасованості або похибки певного вагового вектора може бути сформовано таким чином: Спершу ваги в мережі встановлюються відповідно до цього вагового вектора. Далі, мережа оцінюється за тренувальною послідовністю. Як правило, для представлення похибки поточного вагового вектора використовують суму квадратів різниць між передбаченнями та цільовими значеннями, вказаними в тренувальній послідовності. Потім для мінімізації цієї цільової функції може бути застосовано довільні методики глобальної оптимізації.
Найуживанішим методом глобальної оптимізації для тренування РНМ є генетичні алгоритми, особливо в неструктурованих мережах.[75][76][77]
Спочатку генетичний алгоритм кодується вагами нейронної мережі в наперед визначеному порядку, коли один ген у хромосомі представляє одне зважене з'єднання, і так далі; вся мережа представляється єдиною хромосомою. Функція допасованості обчислюється наступним чином: 1) кожна вага, закодована в хромосомі, призначається відповідному зваженому з'єднанню мережі; 2) потім тренувальний набір зразків представляється мережі, яка поширює вхідні сигнали далі; 3) до функції допасованості повертається середньоквадратична похибка; 4) ця функція потім веде процес генетичного відбору.
Популяцію складають багато хромосом; таким чином, багато різних нейронних мереж еволюціюють, поки не буде досягнуто критерію зупинки. Поширеною схемою зупинки є: 1) коли нейронна мережа засвоїла певний відсоток тренувальних даних, або 2) коли досягнуто мінімального значення середньоквадратичної похибки, або 3) коли було досягнуто максимального числа тренувальних поколінь. Критерій зупинки оцінюється функцією допасованості при отриманні нею оберненого значення середньоквадратичної похибки з кожної з нейронних мереж під час тренування. Отже, метою генетичного алгоритму є максимізувати функцію допасованості, знизивши таким чином середньоквадратичну похибку.
Для пошуку доброго набору ваг можуть застосовуватися й інші методики глобальної (та/або еволюційної) оптимізації, такі як імітація відпалу та метод рою часток.
РНМ можуть поводитися хаотично. В таких випадках для аналізу можна використовувати теорію динамічних систем.
Рекурентні нейронні мережі насправді є рекурсивними нейронними мережами з певною структурою: такою, як в лінійного ланцюжка. В той час як рекурсивні нейронні мережі працюють на будь-якій ієрархічній структурі, поєднуючи дочірні представлення в батьківські, рекурентні нейронні мережі діють на лінійній послідовності часу, поєднуючи попередній такт і приховане представлення в представлення поточного такту.
Рекурентні нейронні мережі, зокрема, можна представляти як нелінійні версії фільтрів зі скінченною та нескінченною імпульсною характеристикою[en], а також як нелінійну авторегресійну екзогенну модель (англ. nonlinear autoregressive exogenous model, NARX).[78]
- Apache Singa[en]
- Caffe: Створена Центром бачення та навчання Берклі (англ. Berkeley Vision and Learning Center, BVLC). Підтримує як ЦП, так і ГП. Розроблена мовою C++, має обгортки для Python та MATLAB.
- Deeplearning4j: Глибоке навчання в Java та Scala на Spark з підтримкою багатьох ГП. Бібліотека глибокого навчання [Архівовано 30 березня 2016 у Wayback Machine.] загального призначення для продуктового стека JVM, що працює на рушії наукових обчислень C++ [Архівовано 11 червня 2018 у Wayback Machine.]. Дозволяє створювати спеціальні шари. Інтегрується з Hadoop та Kafka.
- Keras
- Microsoft Cognitive Toolkit
- TensorFlow: Theano-подібна бібліотека з ліцензією Apache 2.0 з підтримкою ЦП, ГП та запатентованих компанією Google ТП,[79] мобільних
- Theano: Еталонна бібліотека глибокого навчання для Python з ППІ, значною мірою сумісним з популярною бібліотекою NumPy. Дозволяє користувачам писати символічні математичні вирази, потім автоматично породжує їхні похідні, вберігаючи користувача від обов'язку кодувати градієнти або зворотне поширення. Ці символічні вирази автоматично компілюються в CUDA для отримання швидкої реалізації на ГП.
- Torch (www.torch.ch [Архівовано 9 липня 2016 у Wayback Machine.]): Науковий обчислювальний каркас із широкою підтримкою алгоритмів машинного навчання, написаний мовами C та lua. Головним автором є Ронан Коллоберт, наразі застосовується у Facebook AI Research та Twitter.
- Tyagi, Amit Kumar; Abraham, Ajith, ред. (2023). Recurrent neural networks: concepts and applications (1st edition). Boca Raton London New York: CRC Press, Taylor & Francis Group. ISBN 978-1-032-08164-9.
- Salem, Fathi M. (2022). Recurrent Neural Networks: From Simple to Gated Architectures (англ.). Cham: Springer International Publishing, Springer Nature. ISBN 978-3-030-89928-8.
- Talaei Khoei, Tala; Ould Slimane, Hadjar; Kaabouch, Naima (2023-11). Deep learning: systematic review, models, challenges, and research directions. Neural Computing and Applications (англ.) 35 (31). doi:10.1007/s00521-023-08957-4.
- Orojo, Oluwatamilore; Tepper, Jonathan; McGinnity, T. M.; Mahmud, Mufti (1 січня 2023). The Multi-Recurrent Neural Network for State-Of-The-Art Time-Series Processing. Procedia Computer Science 222. doi:10.1016/j.procs.2023.08.187.
- A Review of Recurrent Neural Network-Based Methods in Computational Physiology | IEEE Journals & Magazine. doi:10.1109/tnnls.2022.3145365.
- ↑ A. Graves, M. Liwicki, S. Fernandez, R. Bertolami, H. Bunke, J. Schmidhuber. A Novel Connectionist System for Improved Unconstrained Handwriting Recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 31, no. 5, 2009. (англ.)
- ↑ H. Sak and A. W. Senior and F. Beaufays. Long short-term memory recurrent neural network architectures for large scale acoustic modeling. Proc. Interspeech, pp338-342, Singapore, Sept. 201 (англ.)
- ↑ Goller, C.; Küchler, A. Learning task-dependent distributed representations by backpropagation through structure. Neural Networks, 1996., IEEE. doi:10.1109/ICNN.1996.548916. (англ.)
- ↑ Seppo Linnainmaa[en] (1970). The representation of the cumulative rounding error of an algorithm as a Taylor expansion of the local rounding errors. Master's Thesis (in Finnish), Univ. Helsinki, 6-7. (фін.)
- ↑ Griewank, Andreas and Walther, A.. Principles and Techniques of Algorithmic Differentiation, Second Edition. SIAM, 2008. (англ.)
- ↑ Socher, Richard; Lin, Cliff; Ng, Andrew Y.; Manning, Christopher D. Parsing Natural Scenes and Natural Language with Recursive Neural Networks. The 28th International Conference on Machine Learning (ICML 2011). (англ.)
- ↑ Socher, Richard; Perelygin, Alex; Y. Wu, Jean; Chuang, Jason; D. Manning, Christopher; Y. Ng, Andrew; Potts, Christopher. Recursive Deep Models for Semantic Compositionality Over a Sentiment Treebank (PDF). EMNLP 2013. Архів оригіналу (PDF) за 28 грудня 2016. Процитовано 17 квітня 2017. (англ.)
- ↑ Rául Rojas (1996). Neural networks: a systematic introduction. Springer. с. 336. ISBN 978-3-540-60505-8. (англ.)
- ↑ а б Cruse, Holk; Neural Networks as Cybernetic Systems [Архівовано 20 жовтня 2016 у Wayback Machine.], 2nd and revised edition (англ.)
- ↑ Elman, Jeffrey L. (1990). Finding Structure in Time. Cognitive Science. 14 (2): 179—211. doi:10.1016/0364-0213(90)90002-E. (англ.)
- ↑ Jordan, Michael I. (1986). Serial Order: A Parallel Distributed Processing Approach. (англ.)
- ↑ а б в Tanaka, Gouhei; Yamane, Toshiyuki; Héroux, Jean Benoit; Nakane, Ryosho; Kanazawa, Naoki; Takeda, Seiji; Numata, Hidetoshi; Nakano, Daiju; Hirose, Akira (1 липня 2019). Recent advances in physical reservoir computing: A review. Neural Networks. Т. 115. с. 100—123. doi:10.1016/j.neunet.2019.03.005. ISSN 0893-6080. Процитовано 15 грудня 2023.
- ↑ а б Gauthier, Daniel J.; Bollt, Erik; Griffith, Aaron; Barbosa, Wendson A. S. (21 вересня 2021). Next generation reservoir computing. Nature Communications (англ.). Т. 12, № 1. с. 5564. doi:10.1038/s41467-021-25801-2. ISSN 2041-1723. PMC 8455577. PMID 34548491. Процитовано 15 грудня 2023.
{{cite news}}: Обслуговування CS1: Сторінки з PMC з іншим форматом (посилання) - ↑ H. Jaeger. Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication. Science, 304:78–80, 2004. (англ.)
- ↑ Ma, Qianli; Chen, Weibiao; Wei, Jia; Yu, Zhiwen (1 вересня 2014). Direct model of memory properties and the linear reservoir topologies in echo state networks. Applied Soft Computing. Т. 22. с. 622—628. doi:10.1016/j.asoc.2014.04.038. ISSN 1568-4946. Процитовано 15 грудня 2023.
- ↑ Steiner, Peter; Jalalvand, Azarakhsh; Birkholz, Peter (2023-12). Exploring unsupervised pre-training for echo state networks. Neural Computing and Applications (англ.). Т. 35, № 34. с. 24225—24242. doi:10.1007/s00521-023-08988-x. ISSN 0941-0643. Процитовано 15 грудня 2023.
- ↑ W. Maass, T. Natschläger, and H. Markram. A fresh look at real-time computation in generic recurrent neural circuits. Technical report, Institute for Theoretical Computer Science, TU Graz, 2002. (англ.)
- ↑ Deckers, Lucas; Tsang, Ing Jyh; Van Leekwijck, Werner; Latré, Steven (2022). Extended liquid state machines for speech recognition. Frontiers in Neuroscience. Т. 16. doi:10.3389/fnins.2022.1023470. ISSN 1662-453X. PMC 9651956. PMID 36389242. Процитовано 15 грудня 2023.
{{cite news}}: Обслуговування CS1: Сторінки з PMC з іншим форматом (посилання) Обслуговування CS1: Сторінки із непозначеним DOI з безкоштовним доступом (посилання) - ↑ Mosaic LSM: A Liquid State Machine Approach for Multimodal Longitudinal Data Analysis | IEEE Conference Publication | IEEE Xplore. ieeexplore.ieee.org. doi:10.1109/ijcnn54540.2023.10191256. Процитовано 15 грудня 2023.
- ↑ Real-world Performance Estimation of Liquid State Machines for Spoken Digit Classification | IEEE Conference Publication | IEEE Xplore. ieeexplore.ieee.org. doi:10.1109/ijcnn54540.2023.10191451. Процитовано 15 грудня 2023.
- ↑ Pan, Wenxuan; Zhao, Feifei; Zeng, Yi; Han, Bing (7 жовтня 2023). Adaptive structure evolution and biologically plausible synaptic plasticity for recurrent spiking neural networks. Scientific Reports (англ.). Т. 13, № 1. с. 16924. doi:10.1038/s41598-023-43488-x. ISSN 2045-2322. PMC 10560283. PMID 37805632. Процитовано 15 грудня 2023.
{{cite news}}: Обслуговування CS1: Сторінки з PMC з іншим форматом (посилання) - ↑ а б в Sepp Hochreiter[en] (1991), Untersuchungen zu dynamischen neuronalen Netzen [Архівовано 6 березня 2015 у Wayback Machine.], Diploma thesis. Institut f. Informatik, Technische Univ. Munich. Advisor: J. Schmidhuber. (нім.)
- ↑ а б в г Jürgen Schmidhuber. Learning complex, extended sequences using the principle of history compression. Neural Computation, 4(2):234–242. Online[недоступне посилання] (англ.)
- ↑ Jürgen Schmidhuber (2015). Deep Learning. Scholarpedia, 10(11):32832. Section on Unsupervised Pre-Training of RNNs and FNNs [Архівовано 19 квітня 2016 у Wayback Machine.] (англ.)
- ↑ Jürgen Schmidhuber (1993). Habilitation thesis, TUM, 1993. Page 150 ff demonstrates credit assignment across the equivalent of 1,200 layers in an unfolded RNN. Online[недоступне посилання] (англ.)
- ↑ а б Hochreiter, Sepp[en]; and Schmidhuber, Jürgen; Long Short-Term Memory, Neural Computation, 9(8):1735–1780, 1997 (англ.)
- ↑ Felix Gers, Nicholas Schraudolph, and Jürgen Schmidhuber (2002). Learning precise timing with LSTM recurrent networks. Journal of Machine Learning Research 3:115–143. (англ.)
- ↑ а б в Jürgen Schmidhuber (2015). Deep learning in neural networks: An overview. Neural Networks 61 (2015): 85-117. ArXiv [Архівовано 8 травня 2017 у Wayback Machine.] (англ.)
- ↑ Justin Bayer, Daan Wierstra, Julian Togelius, and Jürgen Schmidhuber (2009). Evolving memory cell structures for sequence learning. Proceedings of ICANN (2), pp. 755—764. (англ.)
- ↑ Santiago Fernandez, Alex Graves, and Jürgen Schmidhuber (2007). Sequence labelling in structured domains with hierarchical recurrent neural networks. Proceedings of IJCAI. (англ.)
- ↑ Alex Graves, Santiago Fernandez, Faustino Gomez, and Jürgen Schmidhuber (2006). Connectionist temporal classification: Labelling unsegmented sequence data with recurrent neural nets. Proceedings of ICML'06, pp. 369—376. (англ.)
- ↑ Santiago Fernandez, Alex Graves, and Jürgen Schmidhuber (2007). An application of recurrent neural networks to discriminative keyword spotting. Proceedings of ICANN (2), pp. 220—229. (англ.)
- ↑ Graves, Alex; and Schmidhuber, Jürgen; Offline Handwriting Recognition with Multidimensional Recurrent Neural Networks, in Bengio, Yoshua; Schuurmans, Dale; Lafferty, John; Williams, Chris K. I.; and Culotta, Aron (eds.), Advances in Neural Information Processing Systems 22 (NIPS'22), December 7th–10th, 2009, Vancouver, BC, Neural Information Processing Systems (NIPS) Foundation, 2009, pp. 545—552 (англ.)
- ↑ Awni Hannun, Carl Case, Jared Casper, Bryan Catanzaro, Greg Diamos, Erich Elsen, Ryan Prenger, Sanjeev Satheesh, Shubho Sengupta, Adam Coates, Andrew Ng (2014). Deep Speech: Scaling up end-to-end speech recognition. arXiv:1412.5567 [Архівовано 21 грудня 2016 у Wayback Machine.] (англ.)
- ↑ Hasim Sak and Andrew Senior and Francoise Beaufays (2014). Long Short-Term Memory recurrent neural network architectures for large scale acoustic modeling. Proceedings of Interspeech 2014. (англ.)
- ↑ Xiangang Li, Xihong Wu (2015). Constructing Long Short-Term Memory based Deep Recurrent Neural Networks for Large Vocabulary Speech Recognition arXiv:1410.4281 [Архівовано 26 вересня 2017 у Wayback Machine.] (англ.)
- ↑ а б Bo Fan, Lijuan Wang, Frank K. Soong, and Lei Xie (2015). Photo-Real Talking Head with Deep Bidirectional LSTM. In Proceedings of ICASSP 2015. (англ.)
- ↑ Heiga Zen and Hasim Sak (2015). Unidirectional Long Short-Term Memory Recurrent Neural Network with Recurrent Output Layer for Low-Latency Speech Synthesis. In Proceedings of ICASSP, pp. 4470-4474. (англ.)
- ↑ Haşim Sak, Andrew Senior, Kanishka Rao, Françoise Beaufays and Johan Schalkwyk (September 2015): Google voice search: faster and more accurate. [Архівовано 9 березня 2016 у Wayback Machine.] (англ.)
- ↑ Felix A. Gers and Jürgen Schmidhuber. LSTM Recurrent Networks Learn Simple Context Free and Context Sensitive Languages. IEEE TNN 12(6):1333–1340, 2001. (англ.)
- ↑ Ilya Sutskever, Oriol Vinyals, and Quoc V. Le (2014). Sequence to Sequence Learning with Neural Networks. arXiv [Архівовано 29 квітня 2017 у Wayback Machine.] (англ.)
- ↑ Rafal Jozefowicz, Oriol Vinyals, Mike Schuster, Noam Shazeer, Yonghui Wu (2016). Exploring the Limits of Language Modeling. arXiv [Архівовано 6 червня 2017 у Wayback Machine.] (англ.)
- ↑ Dan Gillick, Cliff Brunk, Oriol Vinyals, Amarnag Subramanya (2015). Multilingual Language Processing From Bytes. arXiv [Архівовано 26 липня 2017 у Wayback Machine.] (англ.)
- ↑ Oriol Vinyals, Alexander Toshev, Samy Bengio, and Dumitru Erhan (2015). Show and Tell: A Neural Image Caption Generator. arXiv [Архівовано 4 квітня 2017 у Wayback Machine.] (англ.)
- ↑ Bidirectional recurrent neural networks. IEEE Transactions on Signal Processing, 45:2673–81, November 1997. (англ.)
- ↑ A. Graves and J. Schmidhuber. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Networks, 18:602–610, 2005. (англ.)
- ↑ Harvey, Inman; Husbands, P.; Cliff, D. (1994). Seeing the light: Artificial evolution, real vision. Proceedings of the third international conference on Simulation of adaptive behavior: from animals to animats 3: 392—401. (англ.)
- ↑ Quinn, Matthew (2001). Evolving communication without dedicated communication channels. Advances in Artificial Life. Lecture Notes in Computer Science. 2159: 357—366. doi:10.1007/3-540-44811-X_38. ISBN 978-3-540-42567-0. (англ.)
- ↑ Beer, R.D. (1997). The dynamics of adaptive behavior: A research program. Robotics and Autonomous Systems. 20 (2–4): 257—289. doi:10.1016/S0921-8890(96)00063-2. (англ.)
- ↑ R.W. Paine, J. Tani, "How hierarchical control self-organizes in artificial adaptive systems, " Adaptive Behavior, 13(3), 211—225, 2005. (англ.)
- ↑ CiteSeerX — Recurrent Multilayer Perceptrons for Identification and Control: The Road to Applications. Citeseerx.ist.psu.edu. Архів оригіналу за 28 грудня 2013. Процитовано 3 січня 2014. (англ.)
- ↑ C.L. Giles, C.B. Miller, D. Chen, H.H. Chen, G.Z. Sun, Y.C. Lee, «Learning and Extracting Finite State Automata with Second-Order Recurrent Neural Networks» [Архівовано 15 квітня 2021 у Wayback Machine.], Neural Computation, 4(3), p. 393, 1992. (англ.)
- ↑ C.W. Omlin, C.L. Giles, «Constructing Deterministic Finite-State Automata in Recurrent Neural Networks» [Архівовано 18 квітня 2017 у Wayback Machine.] Journal of the ACM, 45(6), 937—972, 1996. (англ.)
- ↑ Y. Yamashita, J. Tani, "Emergence of functional hierarchy in a multiple timescale neural network model: a humanoid robot experiment, " PLoS Computational Biology, 4(11), e1000220, 211—225, 2008. http://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1000220 [Архівовано 5 березня 2022 у Wayback Machine.] (англ.)
- ↑ Alnajjar F, Yamashita Y, Tani J (2013) The Hierarchical and Functional Connectivity of Higher-order Cognitive Mechanisms: Neurorobotic Model to Investigate the Stability and Flexibility of Working Memory, Frontiers in Neurorobotics, 7:2. doi: 10.3389/fnbot.2013.00002 PMID 3575058 (англ.)
- ↑ Graves, Alex; Wayne, Greg; Danihelka, Ivo (2014). Neural Turing Machines (PDF). arXiv:1410.5401. Архів оригіналу (PDF) за 7 червня 2017. Процитовано 17 квітня 2017. (англ.)
- ↑ Guo-Zheng Sun, C. Lee Giles, Hsing-Hen Chen, "The Neural Network Pushdown Automaton: Architecture, Dynamics and Training, " Adaptive Processing of Sequences and Data Structures, Lecture Notes in Computer Science, Volume 1387, 296—345, 1998. (англ.)
- ↑ Kosko, B. (1988). Bidirectional associative memories. IEEE Transactions on Systems, Man, and Cybernetics. 18 (1): 49—60. doi:10.1109/21.87054. (англ.)
- ↑ Rakkiyappan, R.; Chandrasekar, A.; Lakshmanan, S.; Park, Ju H. (2 січня 2015). Exponential stability for markovian jumping stochastic BAM neural networks with mode-dependent probabilistic time-varying delays and impulse control. Complexity. 20 (3): 39—65. doi:10.1002/cplx.21503. (англ.)
- ↑ P. J. Werbos. Generalization of backpropagation with application to a recurrent gas market model. Neural Networks, 1, 1988. (англ.)
- ↑ David E. Rumelhart; Geoffrey E. Hinton; Ronald J. Williams. Learning Internal Representations by Error Propagation. (англ.)
- ↑ A. J. Robinson and F. Fallside. The utility driven dynamic error propagation network. Technical Report CUED/F-INFENG/TR.1, Cambridge University Engineering Department, 1987. (англ.)
- ↑ R. J. Williams and D. Zipser. Gradient-based learning algorithms for recurrent networks and their computational complexity. In Back-propagation: Theory, Architectures and Applications. Hillsdale, NJ: Erlbaum, 1994. (англ.)
- ↑ J. Schmidhuber. A local learning algorithm for dynamic feedforward and recurrent networks. Connection Science, 1(4):403–412, 1989. (англ.)
- ↑ Neural and Adaptive Systems: Fundamentals through Simulation. J.C. Principe, N.R. Euliano, W.C. Lefebvre (англ.)
- ↑ Ollivier, Y. and Tallec, C. and Charpiat, G. (2015). Training recurrent networks online without backtracking. arXiv [Архівовано 6 липня 2017 у Wayback Machine.] (англ.)
- ↑ J. Schmidhuber. A fixed size storage O(n3) time complexity learning algorithm for fully recurrent continually running networks. Neural Computation, 4(2):243–248, 1992. (англ.)
- ↑ R. J. Williams. Complexity of exact gradient computation algorithms for recurrent neural networks. Technical Report Technical Report NU-CCS-89-27, Boston: Northeastern University, College of Computer Science, 1989. (англ.)
- ↑ B. A. Pearlmutter. Learning state space trajectories in recurrent neural networks. Neural Computation, 1(2):263–269, 1989. (англ.)
- ↑ S. Hochreiter[en], Y. Bengio, P. Frasconi, and J. Schmidhuber. Gradient flow in recurrent nets: the difficulty of learning long-term dependencies. In S. C. Kremer and J. F. Kolen, editors, A Field Guide to Dynamical Recurrent Neural Networks. IEEE Press, 2001. (англ.)
- ↑ P. Campolucci, A. Uncini, F. Piazza, B. D. Rao (1999). On-Line Learning Algorithms for Locally Recurrent Neural Networks. IEEE Transaction On Neural Networks. 10 (2): 253—271 — через http://ieeexplore.ieee.org/document/750549/.
{{cite journal}}: Зовнішнє посилання в|via= - ↑ E. A. Wan, F. Beaufays (1996). Diagrammatic derivation of gradient algorithms for neural networks. Neural Computation. 8: 182—201 — через http://www.mitpressjournals.org/doi/abs/10.1162/neco.1996.8.1.182?journalCode=neco#.WJ14jYWcGOw.
{{cite journal}}: Зовнішнє посилання в|via= - ↑ P. Campolucci, A. Uncini, F. Piazza (2000). A Signal-Flow-Graph Approach to On-line Gradient Calculation. Neural Computation. 12: 1901—1927 — через http://www.mitpressjournals.org/doi/abs/10.1162/089976600300015196?journalCode=neco#.WJ16EoWcGOw.
{{cite journal}}: Зовнішнє посилання в|via= - ↑ A. Y. Lee (1974). Signal Flow Graphs-Computer-Aided System Analysis and Sensitivity Calculations. IEEE Transactions on Circuits and Systems. 21: 209—216 — через http://ieeexplore.ieee.org/document/1083832/.
{{cite journal}}: Зовнішнє посилання в|via= - ↑ F. J. Gomez and R. Miikkulainen. Solving non-Markovian control tasks with neuroevolution. Proc. IJCAI 99, Denver, CO, 1999. Morgan Kaufmann. (англ.)
- ↑ Applying Genetic Algorithms to Recurrent Neural Networks for Learning Network Parameters and Architecture. Архів оригіналу за 6 грудня 2010. Процитовано 17 квітня 2017. (англ.)
- ↑ F. Gomez, J. Schmidhuber, R. Miikkulainen. Accelerated Neural Evolution through Cooperatively Coevolved Synapses. Journal of Machine Learning Research (JMLR), 9:937-965, 2008. (англ.)
- ↑ Hava T. Siegelmann, Bill G. Horne, C. Lee Giles, "Computational capabilities of recurrent NARX neural networks, " IEEE Transactions on Systems, Man, and Cybernetics, Part B 27(2): 208—215 (1997). (англ.)
- ↑ Cade Metz (18 травня 2016). Google Built Its Very Own Chips to Power Its AI Bots. Wired. Архів оригіналу за 13 січня 2018. Процитовано 17 квітня 2017. (англ.)
- Mandic, Danilo P. & Chambers, Jonathon A. (2001). Recurrent Neural Networks for Prediction: Learning Algorithms, Architectures and Stability. Wiley. ISBN 0-471-49517-4.
- RNNSharp [Архівовано 4 серпня 2017 у Wayback Machine.] CRF на основі рекурентних нейронних мереж (C#, .NET)
- Recurrent Neural Networks [Архівовано 2 січня 2014 у Wayback Machine.] з понад 60 працями з РНМ від групи Юргена Шмідгубера в Інституті дослідження штучного інтелекту Далле Молле[en] (англ.)
- Реалізація нейронної мережі Елмана [Архівовано 2 лютого 2017 у Wayback Machine.] для WEKA
- Рекурентні нейронні мережі та ДКЧП в Java (англ.)

























