Теорема Баєса

У теорії ймовірностей та статистиці Теоре́ма Ба́єса (або ж Зако́н Ба́єса, чи Правило Баєса) описує ймовірність події, спираючись на обставини, що могли би бути пов'язані з цією подією. Наприклад, припустімо, що хтось цікавиться, чи має рак певна особа, і знає вік цієї особи. Якщо рак пов'язаний з віком, то, застосовуючи теорему Баєса, інформацію про вік осіб можливо використати для точнішої оцінки ймовірності того, що вони мають рак.
При застосуванні задіяні у теоремі Баєса ймовірності можуть мати різні інтерпретації. В одній із цих інтерпретацій теорема Баєса використовується безпосередньо у певному підході до статистичного висновування. При баєсовій інтерпретації ймовірності ця теорема виражає, як повинна раціонально змінюватися суб'єктивна міра впевненості при врахуванні свідчення: це є баєсовим висновуванням, що є фундаментальним для баєсової статистики. Тим не менш, теорема Баєса має численні застосування у широкому спектрі обчислень із залученням ймовірностей, а не лише у баєсовому висновуванні.
Теорему Баєса названо на честь прп. Томаса Баєса ([ˈbeɪz]; 1701—1761), який першим[1] запропонував рівняння, яке дозволяє новим свідченням уточнювати переконання. Її було розвинуто далі П'єром-Симоном Лапласом, який вперше опублікував це сучасне формулювання у своїй праці 1812 року «Аналітична теорія ймовірностей». Сер Гарольд Джеффріс поклав баєсів алгоритм та лапласове формулювання на аксіоматичну основу. Джеффріс писав, що теорема Баєса «є для теорії ймовірностей тим, чим теорема Піфагора є для геометрії».[2]

Теорема Баєса задається математично таким рівнянням:[3]
- ,
де та є подіями.
- та є ймовірностями та безвідносно одна до одної.
- , умовна ймовірність, є ймовірністю події за умови істинності .
- є ймовірністю за умови істинності .
Припустимо, що ми хочемо знати ймовірність того, що якась особа має рак, але ми нічого не знаємо про неї. Незважаючи на відсутність жодних відомостей про особу, якусь імовірність може бути призначено на основі загальної поширеності раку. Заради цього прикладу уявімо, що нею є 1%. Це є відомим як базовий рівень, або апріорна ймовірність мати рак. «Апріорна» відповідає часу до того моменту, як нас буде поінформовано про даний конкретний випадок.
Далі, уявімо, що ми з'ясували, що тій особі 65 років. Якщо припустити, що рак та вік є пов'язаними, то цю нову порцію інформації можна використати для кращої оцінки ризику тієї особи мати рак. Точніше, ми хотіли би знати ймовірність того, що особа має рак, якщо відомо, що їй 65 років. Ця величина є відомою як поточна ймовірність, де «поточна» відповідає теоретичній ситуації після з'ясування інформації про даний конкретний випадок.
Для того, щоби застосувати знання про вік тієї особи в поєднанні з теоремою Баєса, потрібні дві додаткові порції інформації. Зауважте, проте, що ця додаткова інформація не стосується конкретно тієї особи. Потрібна така інформація:
- Ймовірність мати вік 65 років. Припустімо, що нею є 0,2%.
- Ймовірність того, що особа, яка має рак, має вік 65 років. Припустімо, що нею є 0,5%. Зауважте, що вона є більшою за попереднє значення. Це відображає той факт, що люди з раком є непропорційно 65-річними.
Знаючи це, разом із базовим рівнем, ми можемо обчислити, що особа, яка має вік 65 років, має ймовірність мати рак, що дорівнює
Може стати несподіванкою, що хоча перебування у віці 65 років і збільшує ризик мати рак, ймовірність тієї особи мати рак однаково є досить низькою. Це тому, що низьким є базовий рівень раку (незалежно від віку). Це показує як важливість базового рівня, так і те, що ним зазвичай нехтують.[4] Нехтування базовим рівнем призводить до серйозного спотворення інтерпретації статистики; отже, потрібно приділяти особливу увагу тому, щоб уникати таких помилок. Знайомство з теоремою Баєса є одним із шляхів боротьби з природною схильністю нехтувати базовими рівнями.
Задачі із застосуванням теореми Баєса часто легше зрозуміти, застосовуючи задані в задачі умови до великого набору спостережень. Припустімо, наприклад, що якась спільнота складається зі 100 000 людей. Відповідно до умови задачі, 1% цієї генеральної сукупності, або 1 000 людей, матимуть рак. 0,2% від цієї генеральної сукупності, або 200 людей, матимуть вік 65 років. Із 1 000 людей з раком лише 0,5%, або 5 людей, будуть 65-річними. Таким чином, очікується, що з 200 людей, які мають вік 65 років, лише 5 матимуть рак. 5/200 = 2,5%.
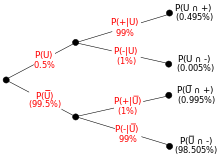
Припустімо, що тест на вживання наркотиків має чутливість 99% та специфічність 99%. Тобто, цей тест даватиме 99% правильних позитивних результатів для тих, хто вживає наркотики, і 99% правильних негативних результатів для тих, хто не вживає. Припустімо, що 0,5% людей вживають наркотики. Якщо для випадково вибраної особи перевірка виявляється позитивною, то якою є ймовірність, що вона вживає наркотики?
Знаменник має таку форму відповідно до Формули повної ймовірності. У даному разі це означає, що ймовірність отримати «чорну мітку» складається із суми двох імовірностей: бути виявленим, якщо ти вживаєш (тут має значення чутливість), і бути «виявленим», хоч ти і «чистий» (а тут — специфічність).
Незважаючи на видиму точність перевірки, все ж якщо індивідуальна перевірка особи дає позитивний результат, то ймовірніше, що ця особа не вживає наркотиків, ніж що вона їх вживає. Це ще раз свідчить про важливість базових рівнів, і як формування політики може бути кричуще помилковим, якщо базовими рівнями нехтують.
Цей несподіваний результат виникає тому, що кількість тих, хто не вживає, є дуже великою у порівнянні з кількістю тих, хто вживає; таким чином, кількість хибних позитивних результатів (0,995%) переважує кількість правильних позитивних результатів (0,495%). На конкретних цифрах, якщо перевірено 1000 осіб, то очікується 995 тих, хто не вживає наркотиків, і 5 тих, хто вживає. Із 995 тих, хто не вживає, очікується 0,01 × 995 ≃ 10 хибних позитивних результатів. Із 5 тих, хто вживає, очікується 0,99 × 5 ≃ 5 правильних позитивних результатів. Із 15 позитивних результатів лише 5, близько 33%, є істинними.
Примітка: Важливість специфічності може бути проілюстровано показуванням, що навіть якщо чутливість є 100%, а специфічність є 99%, то ймовірність того, що особа вживає наркотики, є ≈33%, але якщо специфічність змінюється до 99,5%, а чутливість падає до 99%, то ймовірність того, що особа вживає наркотики, виростає до 49,8%.
Вся продукція заводу виробляється на трьох верстатах. На ці три верстати приходяться 20%, 30% та 50% продукції відповідно. Частка бракованих виробів є такою: 5% для першого верстата, 3% для другого верстата та 1% для третього. Якщо виріб, вибраний навмання із загального обсягу продукції, виявився бракованим, то якою є ймовірність того, що його було зроблено на третьому верстаті?
Розв'язання є таким. Нехай позначає подію, що випадково вибраний виріб було зроблено на -тому верстаті (для ). Нехай позначає подію, що випадково вибраний виріб є бракованим. Тоді ми маємо наступну інформацію:
Якщо виріб було зроблено на верстаті , то ймовірністю його бракованості є 0,05, тобто . Загалом ми маємо
Для отримання відповіді на початкове запитання ми спочатку знаходимо . Це можна зробити наступним чином:
Отже, 2,4% загального обсягу продукції заводу є бракованими.
Нам задано, що сталося, і ми хочемо обчислити умовну ймовірність . За теоремою Баєса
- .
За умови бракованості виробу ймовірністю того, що його виготовили на третьому верстаті, є лише 5/24. Незважаючи на те, що верстат 3 виробляє половину загального обсягу продукції, він видає значно меншу частку бракованих виробів. Тому знання того, що вибраний виріб є бракованим, дозволяє нам замінити апріорну ймовірність меншою апостеріорною ймовірністю .
Знову ж таки, цієї відповіді можна досягнути без вдавання до формули, шляхом застосування умов до будь-якого гіпотетичного числа випадків. Наприклад, у 100 000 виробах, вироблених заводом, 20 000 буде вироблено верстатом A, 30 000 — верстатом B, і 50 000 — верстатом C. Верстат A виробить 1 000 бракованих виробів, верстат B — 900, а верстат C — 500. Із загального числа 2 400 бракованих виробів лише 500, або 5/24, буде вироблено верстатом C.

Інтерпретація теореми Баєса залежить від інтерпретацій імовірності, що приписуються її членам. Нижче описано дві головні інтерпретації.
У баєсовій (або епістемологічній) інтерпретації ймовірність вимірює міру впевненості. Теорема Баєса, таким чином, пов'язує міру впевненості у висловленні до та після врахування свідчення. Наприклад, припустімо, що вважається із впевненістю 50%, що монета вдвічі ймовірніше падає гербом, ніж номіналом. Якщо монету підкидають кілька разів та спостерігають результати, то міра впевненості може рости, зменшуватися чи залишатися незмінною залежно від результатів.
Для висловлення та свідчення
- , апріорна, — це початкова міра впевненості в .
- , апостеріорна, — це міра впевненості із врахуванням .
- частка представляє підтримку, що її надає для .
Для подальшої інформації про застосування теореми Баєса при баєсовій інтерпретації ймовірності див. баєсове висновування.

У частотницькій інтерпретації ймовірність вимірює частку результатів. Наприклад, припустімо, що експеримент проводиться багато разів. є часткою результатів із властивістю , а — із властивістю . є часткою результатів із властивістю серед результатів із властивістю , а — часткою тих, що з серед тих, що з .
Роль теореми Баєса найкраще візуалізується за допомогою деревоподібних схем, як показано праворуч. Ці дві діаграми розділюють одні й ті самі результати за та у протилежному порядку, для отримання зворотних ймовірностей. Теорема Баєса слугує зв'язком між цими двома розділюваннями.

Ентомолог спостерігає за, можливо, рідкісним підвидом жука, оскільки у жука є візерунок на спині. Відомо, що 98 % жуків з рідкісного підвиду мають цей візерунок, або, формально, P(Візерунок|Рідкісний) = 98 %. У поширеного підвиду цей візерунок мають 5 % створінь. Рідкісний підвид налічує лише 0,1 % від популяції двох видів. Наскільки ймовірно, що жук з візерунком, за яким спостерігає ентомолог, є рідкісним? Тобто, чому дорівнює P(Рідкісний|Візерунок)?
Скористаємося розширеною формою теореми Баєса (оскільки будь-який жук популяції може бути лише рідкісним або поширеним):
Тобто, ймовірність того, що ентомолог спостерігає саме рідкісний підвид жука — незначна, а саме 1,9 % або 0,019.
Для подій та , за умови, що ,
У багатьох застосуваннях, наприклад, у баєсовому висновуванні, подія під час розгляду є фіксованою, і ми хочемо розглядати вплив того, що трапилося її спостереження, на нашу впевненість у різних можливих подіях . У такій ситуації знаменник крайнього виразу, ймовірність заданого свідчення , є фіксованим, а варіювати ми хочемо . Тоді теорема Баєса показує, що апостеріорні ймовірності є пропорційними до чисельника:
- (пропорційність за для заданого ).
Словами: апостеріорне пропорційне апріорній кількості разів правдоподібності.[5]
Якщо події є взаємовиключними та вичерпними, тобто, одна з них точно відбувається, але жодні дві не можуть відбуватися одночасно, і ми знаємо їхні ймовірності з точністю до пропорційності, то ми можемо визначити коефіцієнт пропорційності, використовуючи той факт, що їхні ймовірності повинні давати в сумі одиницю. Наприклад, для заданої події сама подія та її доповнення є взаємовиключними та вичерпними. При позначенні коефіцієнту пропорційності через ми маємо
- та
Шляхом додавання цих двох формул ми виводимо
Іншою формою теореми Баєса, що звичайно зустрічається при розгляді двох конкурентних тверджень або гіпотез, є
Для епістемологічної інтерпретації:
Для висловлення та свідчення або передумови ,[6]
- , апріорна ймовірність, є початковою мірою впевненості в .
- є відповідною ймовірністю початкової міри впевненості проти :
- , умовна ймовірність або правдоподібність, є мірою впевненості в за умови істинності висловлення .
- , умовна ймовірність або правдоподібність, є мірою впевненості в за умови хибності висловлення .
- , апостеріорна ймовірність, є ймовірністю після врахування за та проти .
Часто для деякого розбиття простору вибірки цей простір подій задається або умоглядно представляється у термінах та . У такому випадку зручно обчислювати із використанням закону повної ймовірності:
В окремому випадку, коли є двійковою змінною[en]:

Розгляньмо простір подій , породжуваний двома випадковими змінними та . В принципі, теорема Баєса застосовується до подій та . Однак, члени стають нульовими у точках, де будь-яка зі змінних має скінченну густину імовірності. Щоби теорема Баєса залишалася придатною, її може бути сформульовано у термінах доречних густин (див. Виведення).
Якщо є безперервною, а — дискретною,
- .
Якщо є дискретною, а — безперервною,
- .
Якщо як , так і є безперервними,
- .

Безперервний простір подій часто представляється у термінах чисельників. Часто зручно виключати знаменник, використовуючи закон повної ймовірності. Для це стає інтегралом
- .
Правило Баєса — це теорема Баєса у формі шансів[en].
де
називається коефіцієнтом Баєса, або відношенням правдоподібності, і шанси між двома подіями є просто відношенням ймовірностей цих двох подій. Отже,
- ,
- .
Таким чином, це правило говорить, що апостеріорні шанси є апріорними шансами, помноженими на коефіцієнт Баєса, або, іншими словами, апостеріорне пропорційне апріорній кількості разів правдоподібності.
Теорему Баєса може бути виведено з визначення умовної ймовірності:
- , якщо ,
- , якщо ,
- ,
- , якщо .
Для двох безперервних випадкових змінних та теорему Баєса може бути виведено аналогічно з визначення умовної густини:
- .
Теорему Баєса названо на честь преподобного Томаса Баєса (1701—1761), який вивчав, як обчислювати розподіл для параметру ймовірності біноміального розподілу (у сучасній термінології). Неопублікований рукопис Баєса було суттєво відредаговано Річардом Прайсом[en] до того, як його було посмертно прочитано в Королівському товаристві. Прайс відредагував[7] головну працю Баєса, «Есе щодо розв'язання задачі у Доктрині шансів[en]» (1763), що з'явилася в журналі Philosophical Transactions, і містить теорему Баєса. Прайс написав передмову до цієї праці, що подає дещо з філософських основ баєсової статистики. У 1765 році його було обрано Членом Королівського товариства, на визнання його праці над спадком Баєса.[8][9]
Французький математик П'єр-Симон Лаплас відтворив та узагальнив результати Баєса у 1774 році, очевидно, не підозрюючи про працю Баєса.[10][11] Стівен Стіглер[en] у 1983 році висловив думку, що теорему Баєса було відкрито Ніколасом Сондерсоном[en] за деякий час до Баєса.[12] Проте ця інтерпретація була спірною.[13]
Мартін Купер[14] та Шарон Мак-Грейн[15] стверджують, що внесок Річарда Прайса[en] був істотним:
| За сучасними стандартами ми повинні посилатися на правило Баєса — Прайса. Прайс відкрив працю Баєса, усвідомив її важливість, виправив її, вніс до статті, та знайшов їй застосування. Сучасний звичай використовувати саме лише ім'я Баєса є несправедливим, але він настільки вкорінився, що все інше має мало сенсу.[15] Оригінальний текст (англ.)
By modern standards, we should refer to the Bayes–Price rule. Price discovered Bayes's work, recognized its importance, corrected it, contributed to the article, and found a use for it. The modern convention of employing Bayes's name alone is unfair but so entrenched that anything else makes little sense. |
- ↑ Bayes, Mr; Price, Mr (1763). "An Essay towards Solving a Problem in the Doctrine of Chances. By the Late Rev. Mr. Bayes, F. R. S. Communicated by Mr. Price, in a Letter to John Canton, A. M. F. R. S". Philosophical Transactions of the Royal Society of London. 53: 370–418.
- ↑ Jeffreys, Harold (1973). Scientific Inference (вид. III). Cambridge University Press. с. 31. ISBN 978-0-521-18078-8. (англ.)
- ↑ Stuart, A.; Ord, K. (1994), Kendall's Advanced Theory of Statistics: Volume I—Distribution Theory, Edward Arnold[en], §8.7 (англ.)
- ↑ Daniel Kahneman (25 жовтня 2011). Thinking, Fast and Slow. Macmillan. ISBN 978-1-4299-6935-2. Процитовано 8 квітня 2012. (англ.)
- ↑ Lee, Peter M. (2012). Bayesian Statistics. Wiley. ISBN 978-1-1183-3257-3. (англ.)
- ↑ Bayes Theorem: Introduction. Trinity University. Архів оригіналу за 7 серпня 2014. Процитовано 22 березня 2015. [Архівовано 2014-08-07 у Wayback Machine.] (англ.)
- ↑ Richard Allen (1999). David Hartley on Human Nature. SUNY Press. с. 243—4. ISBN 978-0-7914-9451-6. Процитовано 16 червня 2013. (англ.)
- ↑ Holland, pp. 46–7. (англ.)
- ↑ Richard Price (1991). Price: Political Writings. Cambridge University Press. с. xxiii. ISBN 978-0-521-40969-8. Процитовано 16 червня 2013. (англ.)
- ↑ Лаплас вдосконалював теорему Баєса протягом десятиліть:
- Лаплас оголосив про своє незалежне відкриття теореми Баєса у праці Laplace (1774) "Mémoire sur la probabilité des causes par les événements," Mémoires de l'Académie royale des Sciences de MI (Savants étrangers), 4: 621–656. Передруковано у: Laplace, Oeuvres complètes (Paris, France: Gauthier-Villars et fils, 1841), vol. 8, pp. 27–65. Доступно інтерактивно на: Gallica. (фр.) Теорема Баєса з'являється на стор. 29.
- Лаплас представив вдосконалення теореми Баєса у праці Laplace (прочитано: 1783 / опубліковано: 1785) "Mémoire sur les approximations des formules qui sont fonctions de très grands nombres," Mémoires de l'Académie royale des Sciences de Paris, 423–467. Передруковано у: Laplace, Oeuvres complètes (Paris, France: Gauthier-Villars et fils, 1844), vol. 10, pp. 295–338. Доступно інтерактивно на: Gallica. (фр.) Теорему Баєса наведено на сторінці 301.
- Див. також: Laplace, Essai philosophique sur les probabilités (Paris, France: Mme. Ve. Courcier [Madame veuve (тобто, вдова) Courcier], 1814), page 10. (фр.) Англомовний переклад: Pierre Simon, Marquis de Laplace with F. W. Truscott and F. L. Emory, trans., A Philosophical Essay on Probabilities (New York, New York: John Wiley & Sons, 1902), page 15. (англ.)
- ↑ Daston, Lorraine (1988). Classical Probability in the Enlightenment. Princeton Univ Press. с. 268. ISBN 0-691-08497-1. (англ.)
- ↑ Stigler, Stephen M (1983). Who Discovered Bayes' Theorem?. The American Statistician. 37 (4): 290—296. doi:10.1080/00031305.1983.10483122. (англ.)
- ↑ Edwards, A. W. F. (1986). Is the Reference in Hartley (1749) to Bayesian Inference?. The American Statistician. 40 (2): 109—110. doi:10.1080/00031305.1986.10475370. (англ.)
- ↑ Hooper, Martyn (2013). Richard Price, Bayes' theorem, and God. Significance. 10 (1): 36—39. doi:10.1111/j.1740-9713.2013.00638.x. (англ.)
- ↑ а б McGrayne, S. B. (2011). The Theory That Would Not Die: How Bayes' Rule Cracked the Enigma Code, Hunted Down Russian Submarines & Emerged Triumphant from Two Centuries of Controversy. Yale University Press. ISBN 978-0-300-18822-6. (англ.)
- Гнєденко Б. В. Курс теорії ймовірностей. — Київ : ВПЦ Київський університет, 2010. — 464 с.
- Карташов М. В. Імовірність, процеси, статистика. — Київ : ВПЦ Київський університет, 2007. — 504 с.
- Гихман И. И., Скороход А. В., Ядренко М. В. Теория вероятностей и математическая статистика. — Київ : Вища школа, 1988. — 436 с.(рос.)
- Bruss, F. Thomas (2013), "250 years of 'An Essay towards solving a Problem in the Doctrine of Chance. By the late Rev. Mr. Bayes, communicated by Mr. Price, in a letter to John Canton, A. M. F. R. S.' ", DOI 10.1365/s13291-013-0077-z, Jahresbericht der Deutschen Mathematiker-Vereinigung, Springer Verlag, Vol. 115, Issue 3-4 (2013), 129-133. (англ.)
- Gelman, Andrew; Carlin, John B.; Stern, Hal S.; Dunson, David B.; Vehtari, Aki; Rubin, Donald B. (2013). Bayesian Data Analysis (вид. III). CRC Press. ISBN 978-1439840955. (англ.)
- Grinstead, CM and Snell, JL (1997), "Introduction to Probability (2nd edition)", American Mathematical Society (free pdf available) [1]. (англ.)
- Hazewinkel, Michiel, ред. (2001), formula Bayes formula, Математична енциклопедія, Springer, ISBN 978-1-55608-010-4 (англ.)
- McGrayne, SB (2011). The Theory That Would Not Die: How Bayes' Rule Cracked the Enigma Code, Hunted Down Russian Submarines & Emerged Triumphant from Two Centuries of Controversy. Yale University Press. ISBN 978-0-300-18822-6. (англ.)
- Laplace, P (1774/1986), "Memoir on the Probability of the Causes of Events", Statistical Science 1(3):364–378. (англ.)
- Lee, PM (2012), "Bayesian Statistics: An Introduction", Wiley. (англ.)
- Rosenthal, JS (2005), "Struck by Lightning: the Curious World of Probabilities". Harper Collings. (англ.)
- Stigler, SM (1986). Laplace's 1774 Memoir on Inverse Probability. Statistical Science. 1 (3): 359—363. doi:10.1214/ss/1177013620. (англ.)
- Stone, JV (2013), download chapter 1 of "Bayes' Rule: A Tutorial Introduction to Bayesian Analysis", Sebtel Press, England. (англ.)
- Зельнер А. Байесовские методы в эконометрии. — М.: Статистика, 1980. — 438 с. (рос.)
- Bayes's theorem в онлайн-версії «Encyclopædia Britannica». (англ.)
- The Theory That Would Not Die by Sharon Bertsch McGrayne New York Times Book Review by John Allen Paulos[en] on 5 August 2011 (англ.)
- Візуальне пояснення Баєса з використанням дерев на YouTube (англ.) (укр.)
- Візуальне пояснення частотницької інтерпретації Баєса на YouTube (англ.)
- Найраніші відомі використання деяких слів математики (B). Містить витоки "Bayesian", "Bayes' Theorem", "Bayes Estimate/Risk/Solution", "Empirical Bayes" та "Bayes Factor". (англ.)
- Weisstein, Eric W. Bayes' Theorem(англ.) на сайті Wolfram MathWorld.
- Bayes' theorem на PlanetMath.(англ.)
- Bayes Theorem and the Folly of Prediction (англ.)
- A tutorial on probability and Bayes' theorem devised for Oxford University psychology students (англ.)
- An Intuitive Explanation of Bayes' Theorem by Eliezer S. Yudkowsky (англ.)
- «Пропорции — ключ к теореме Байеса» (рос.) — переклад статті Understanding Bayes Theorem With Ratios | BetterExplained(англ.)









![{\displaystyle {\begin{aligned}P({\text{вживає}}\mid {\text{+}})&={\frac {P({\text{+}}\mid {\text{вживає}})\times P({\text{вживає}})}{P({\text{+}})}}\\&={\frac {P({\text{+}}\mid {\text{вживає}})\times P({\text{вживає}})}{P({\text{+}}\mid {\text{вживає}})\times P({\text{вживає}})+P({\text{+}}\mid {\text{не вживає}})\times P({\text{не вживає}})}}\\[8pt]&={\frac {0,99\times 0,005}{0,99\times 0,005+0,01\times 0,995}}\\[8pt]&\approx 33,2\%\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0fc56d5788fe6f92ab1238ff24be581545b41ec8)













![{\displaystyle {\begin{aligned}&P({\text{Рідкісний}}\mid {\text{Візерунок}})={\frac {P({\text{Візерунок}}\mid {\text{Рідкісний}})P({\text{Рідкісний}})}{P({\text{Візерунок}})}}=\\[8pt]&={\frac {P({\text{Візерунок}}\mid {\text{Рідкісний}})P({\text{Рідкісний}})}{P({\text{Візерунок}}\mid {\text{Рідкісний}})P({\text{Рідкісний}})+P({\text{Візерунок}}\mid {\text{Поширений}})P({\text{Поширений}})}}=\\[8pt]&={\frac {0,98\times 0,001}{0,98\times 0,001+0,05\times 0,999}}\approx 1,9\%\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70fb572ffcfd27ba9cf87ece6085bee9f59113e1)







































