Теорема Лохса

В теорії чисел, теорема Лохса — теорема про швидкість збіжності розкладу ланцюгового дробу типового дійсного числа. Доведення теореми було опубліковано Ґуставом Лохсом в 1964 році.

Теорема стверджує, що для практично всіх дійсних чисел в інтервалі (0,1) кількість членів m у розкладі ланцюгового дробу цього числа, необхідних для визначення перших n місць десяткового зображення числа асимптотично поводисться як:

$\lim _{n\to \infty }{\frac {m}{n}}={\frac {6\ln(2)\ln(10)}{\pi ^{2}}}\approx 0.97027014$ послідовність A086819 з Онлайн енциклопедії послідовностей цілих чисел, OEIS.

Оскільки ця межа лише трохи менша одиниці, що можна інтерпретувати як те, що кожен додатковий термін у розкладі ланцюгового дробу «типового» дійсного числа збільшує точність наближення приблизно на одну десяткову позицію. Десяткова система є останньою позиційною системою запису, для якої кожна цифра містить менше інформації, ніж одна частка (коефіцієнт) ланцюгового дробу; перехід до 11-вої бази (зміна $\ln(10)$ на $\ln(11)$у рівнянні) робить вищевказане значення більшим одиниці.

Три типові числа, і золотий перетин. Типові числа знаходяться на лінії приблизно 45°, оскільки кожен коефіцієнт ланцюгового дробу дає приблизно одну десяткову цифру. Золотий претин з іншого боку, — це число, яке вимагає більшої кількости коефіцієнтів для кожної цифри

Відносно цього ліміту,

${\frac {\pi ^{2}}{6\ln(2)\ln(10)}}\approx 1.03064083$ послідовність A062542 з Онлайн енциклопедії послідовностей цілих чисел, OEIS,

є вдвічі більшою за десятковий логарифм сталої Леві.

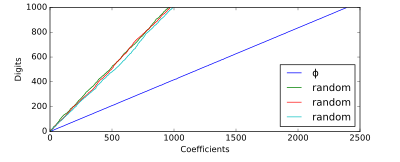
Яскравим прикладом числа, що не проявляє такої поведінки, є золотий перетин - іноді відоме як «найбільш ірраціональне» число — коефіцієнти ланцюгового дробу якого — всі одиниці, найменші можливі в канонічній формі. У середньому йому потрібно приблизно 2.39 коефіцієнтів ланцюгового дробу на кожну десяткову цифру