Циклогон
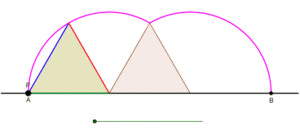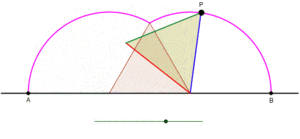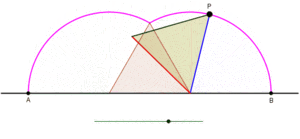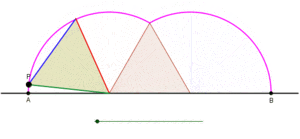
Циклогон — крива, окреслена вершиною многокутника, який котиться без ковзання по прямій.[1][2] Щодо характеру многокутника обмежень немає. Це може бути правильний многокутник, наприклад рівносторонній трикутник або квадрат. Многокутник не обов'язково має бути опуклим: це може бути навіть зіркоподібний многокутник[джерело?]. У загальнішому плані також розглядають криві, прокреслені точками, відмінними від вершин. У таких випадках вважають, що точка трасування жорстко прикріплена до многокутника[джерело?]. Якщо точка трасування розташована за межами многокутника, то криву називають витягнутим циклогоном, а якщо вона лежить всередині многокутника — кривоподібним циклогоном[джерело?].
Коли кількість сторін правильного многокутника збільшується до нескінченності, циклогон стає циклоїдою.[3]
Площа циклогона має цікаву властивість.[3] Нехай A — площа області між прямою та однією з дуг, P — площа многокутника, який котиться, та C — площа круга, обмеженого описаним навколо многокутника колом. Для кожного циклогона, утвореного правильним многокутником,
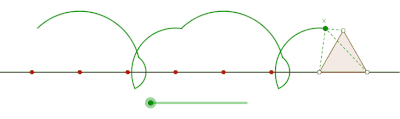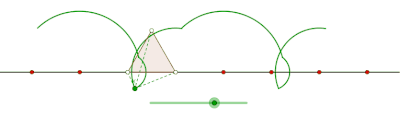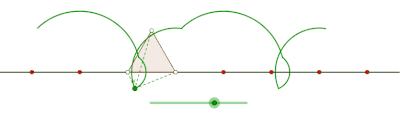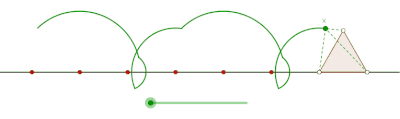
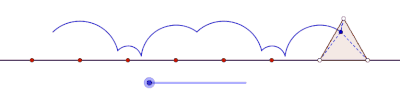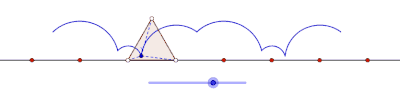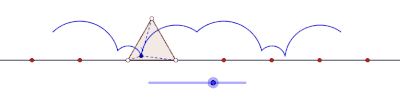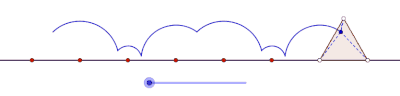
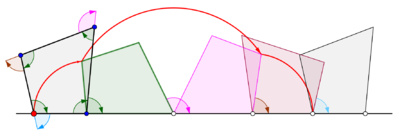
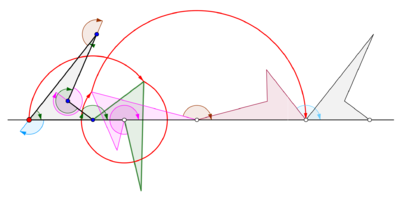
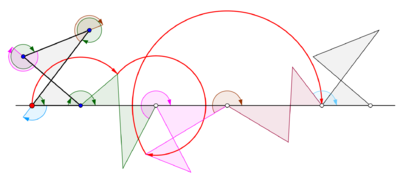
Циклогон виникає, коли многокутник котиться по прямій. Припустимо, що правильний многокутник перекочується сторнами іншого многокутника. Нехай також точка трасування лежить не на межі многокутника, а всередині нього або поза ним, але в площині многокутника. У цій загальнішій ситуації нехай криву описує точка z на правильному многокутному диску[прояснити] з n сторонами, що обертається навколо іншого правильного многокутного диска з m сторін. Нехай сторони цих многокутників мають однакову довжину. Точка z, жорстко прикріплена до n-кутника, викреслить лінію, що складається з n дуг кіл, перш ніж почне періодично повторюватися. Цю криву називають трохогоном — епітрохогоном, якщо n-кутник котиться поза m-кутником, і гіпотрохогоном, якщо він котиться всередині m-кутника. Трохогон є вигнутим[прояснити], якщо z дежить усередині n-кутника, і витягнутим[прояснити] (з петлями), якщо z лежить поза n-кутником. Якщо z збігається з вершиною, то утворюється епіциклогон або гіпоциклогон.[4]
- ↑ Tom M. Apostol, Mamikon Mnatsakanian (2012). New Horizons in Geometry. Mathematical Association of America. с. 68. ISBN 9780883853542.
- ↑ Ken Caviness. Cyclogons. Wolfram Demonstrations Project. Процитовано 23 грудня 2015.
- ↑ а б T. M. Apostol and M. A. Mnatsakanian (1999). Cycloidal Areas without Calculus (PDF). Math Horizons. 7 (1): 12—16. doi:10.1080/10724117.1999.12088451. Архів оригіналу (PDF) за 30 січня 2005. Процитовано 23 грудня 2015.
- ↑ Tom M. Apostopl and Mamikon A. Mnatsaknian (September 2002). Generalized Cyclogons (PDF). Math Horizons. Архів оригіналу (PDF) за 30 січня 2005. Процитовано 23 грудня 2015.