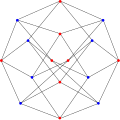
Граф Гофмана

Граф Гофмана
Названо на честь	Алан Гофмана
Вершин	16
Ребер	32
Радіус	3
Діаметр	4
Обхват	4
Автоморфізм	48 ($\mathbb {Z} /2\mathbb {Z} \times S_{4}$)
Хроматичне число	2
Хроматичний індекс	4
Число черг	2
Властивості	гамільтонів двочастковий досконалий ейлерів

Граф Гофмана — 4-регулярний граф із 16 вершинами та 32 ребрами, який відкрив Алан Гофман і опублікував 1963 року. Граф коспектральний графу гіперкуба Q₄.

Граф Гофмана має багато спільних властивостей з гіперкубом Q₄ — обидва гамільтонові і мають хроматичне число 2, хроматичний індекс 4, обхват 4 і діаметр 4. Граф також 4-вершинно-зв'язний і 4-реберно-зв'язний. Проте радіус графа Гофмана дорівнює 3 на відміну від гіперкуба Q_4, радіус якого дорівнює 4. Граф Гофмана не є дистанційно-регулярним. Граф має книжкову товщину 3 та число черг 2.

Алгебричні властивості

Граф Гофмана не є вершинно-транзитивним і його повна група автоморфізмів є групою порядку 48, ізоморфною прямому добутку симетричної групи S₄ і циклічної групи Z/2Z.

Характеристичний многочлен графа Гофмана дорівнює

$(x-4)(x-2)^{4}x^{6}(x+2)^{4}(x+4)$ ,

що робить його цілим графом — графом, спектр якого складається тільки з цілих чисел. Це той самий спектр, що й у гіперкуба Q₄.

Галерея

• 
  Граф Гофмана гамільтонів.
• 
  Хроматичне число графа Гофмана дорівнює 2.
• 
  Хроматичний індекс графа Гофмана дорівнює 4.