Другий закон термодинаміки

Другий закон термодинаміки
Похідна робота	межа Бремерманна
Попередник	перший закон термодинаміки
Наступник	третій закон термодинаміки
Першовідкривач або винахідник	Саді Карно
Дата відкриття (винаходу)	1824

Дру́гий зако́н термодина́міки у сучасному викладі формулюється як об'єднаний принцип існування та зростання деякої функції стану термодинамічної системи — ентропії і вводить поняття абсолютної термодинамічної температури. Таким чином, другий закон являє собою закон про ентропію та її властивості

У ізольованій системі ентропія або залишається незмінною, або зростає в нерівноважних процесах, досягаючи максимуму при встановленні термодинамічної рівноваги (закон зростання ентропії)

Термін ентропія був утворений Р. Клаузіусом зі слова τροπη — перетворення, і приставки — в, всередину, в цілому, звернення всередину . Поняття ентропії, точніше термодинамічної або теплової ентропії є ненаглядним, абстрактним і важким для безпосереднього сприйняття, оскільки безпосередньо не випливає з її математичного вираження. Зрозуміти та відчути глибокий фізичний сенс ентропії легше за початковими формулюваннями другого закону термодинаміки, які є окремими випадками більш загального сучасного формулювання.

Перші формулювання другого закону відносяться до середини XIX століття, коли сфера дії термодинаміки обмежувалася простими процесами перетворення енергії, в основному процесами перетворення тепла в роботу. Надалі сфера впливу законів термодинаміки розширювалася і стала охоплювати фізичні, хімічні, біологічні, ядерні, космічні і інші процеси. У зв'язку з цим формулювання другого закону термодинаміки набуло більш загального, формалізованого характеру, і, як наслідок, менш доступного для широкого кола читачів. Слід також відмітити, що другий закон термодинаміки є найбільш складним, заплутаним і дискусійним питанням. Це обумовлено, з одного боку, складністю змісту самого об'єкту дослідження — сукупності термодинамічних систем, що утворюють в цілому нерівноважну систему, а, з іншого боку, багатозначністю термінів основних понять термодинаміки, що вводяться в інших розділах термодинаміки та в суміжних науках і використовуються при викладі другого закону.. Історія відкриття другого закону термодинаміки являє собою одну з найбільш чудових, повну драматизму, глав загальної історії науки, останні сторінки якої ще далеко не дописані. Знадобилися зусилля не одного, а багатьох національних геніїв, для того щоб відкрити завісу над сокровенною таємницею природи, яку ми називаємо зараз другим законом термодинаміки .

Вихідні побудови другого закону класичної термодинаміки виникли в результаті спроб розробки загальної теорії [тепловий двигун | теплових двигунів]. Перша здогадка про існування особливого принципу, що визначає закономірності перетворення тепла в роботу, була висловлена Саді Карно в дослідженні «Роздуми про рушійну силу вогню і про машини, здатні розвивати цю силу» (1824 р.), написаному до відкриття принципу еквівалентності і загального визнання закону збереження енергії. У цій роботі Саді Карно досліджує умови найвигіднішої роботи теплових двигунів при наявності двох джерел постійних температур: нагрівача і холодильника (Теорема Карно). Він приходить до висновку, що мала величина цього ефекту —— коефіцієнта корисної дії (ККД) — обумовлюється не технічною недосконалістю теплових двигунів, а особливою закономірністю, принципом, що визначає перетворення тепла в роботу:

При постійній температурі неможливо тепло, отримане від тіла, перетворити в роботу, не зробивши при цьому ніяких змін в самому тілі або в інших навколишніх тілах..

У своїх міркуваннях Саді Карно розвиває ідею про кругові процеси (цикли), розробляє схему циклу, що носить його ім'я, вводить поняття про зворотні процеси і формулює теорему Карно:

ККД зворотних теплових машин не залежить від виду термодинамічного циклу і природи робочої речовини, а цілком визначається лише в залежності від температур зовнішніх джерел — нагрівача ($t_{1}$) і холодильника ($t_{2}$)

Свої висновки Карно зробив на підставі помилкової теплородної теорії (теоріі теплеця) і гідравлічної аналогії. Уявлення про теплород, (теплець) як про деяку невагому теплову рідину, були остаточно залишені незабаром після опублікування роботи Карно. Розвиваючи ідеї Карно Рудольф Клаузіус (1850 р.) і Вільям Томсон, (1852 р.) узгодили теорему Карно із законом збереження енергії. Разом з тим P. Клаузіус отримав нові результати, що склали зміст другого закону класичної термодинаміки. . Другий закон термодинаміки, так само, як і перший, є узагальненням загальнолюдського досвіду. (Надалі мова йтиме про звичайні, тобто найпоширеніші, термодинамічні системи, на відміну від незвичайних — спінових систем, що рідко зустрічаються, і про які буде згадано окремо).

Первинні формулювання другого закону термодинаміки і їх коротка характеристика

1.Формулювання Клаузіуса (1850).

Тепло не може переходити само собою від холоднішого тіла до теплішого. .

Формулювання Клаузіуса отримало широке поширення в підручниках фізики і термодинаміки завдяки своїй простоті і наочності, проте ця простота оманлива. Насправді Клаузіус надалі сформулював свій постулат трохи інакше, ніж наведено вище, розшифрувавши що́ мається на увазі під вираженням само собою, яке нерідко опускається. У формулюванні Клаузіуса багато авторів убачають, головним чином, відповідь на питання про напрям природного теплообміну між тілами або термодинамічними системами. Проте, напрямок процесів перенесення речовини, енергії і тепла встановлюють раніше відкриті градієнтні закони, зокрема закон Фур'є, у відношенні до перенесення тепла від гарячого тіла до холодного. У цьому сенсі другий закон нічого не додає до закону Фур'є, окрім слів само собою. Клаузіус у своїх статтях дає чітке роз'яснення цього виразу. В певних умовах тепло може переходити від холодного тіла до гарячого, якщо одночасно в системі відбувається інший, протилежний процес передачі тепла або роботи, який, за словами Клаузіуса, розглядається як компенсація переходу тепла від холоднішого тіла до теплішого. Клаузіус в пізніших роботах уточнює своє формулювання:

Тепло не може переходити само собою (без компенсації) від холоднішого тіла до теплішого.

У цьому полягає основна відмінність другого закону термодинаміки від градієнтних законів.

2. Формулювання В. Томсона (1851).

Неможливо за допомогою неживого матеріального агента отримати від будь-якої маси речовини механічну роботу за допомогою охолодження її нижче температури найхолоднішого з навколишніх предметів .

Це твердження В. Томсона переформулював М. Планк:

3. Формулювання Томсона ─ Планка (1851 р.)

Неможливо побудувати періодично діючу машину, вся дія якої зводилася б до підняття деякого вантажу та охолодженню теплового джерела.

Формулювання Томсона — Планка є більш точним, ніж формулювання Томсона, оскільки у ряді випадків процес отримання роботи при охолодженні джерела тепла нижче температури довкілля є можливим. Наприклад, якщо з джерела тепла, що має температуру довкілля, випустити стислий газ під поршень циліндра або в сопло турбіни, то, розширюючись, газ виконає роботу, причому температура його знизиться і стане нижче температури довкілля. Однак цей приклад не суперечить другому закону термодинаміки, оскільки зазначений процес є незамкненим, і, якщо його замкнути, тобто привести робоче тіло у вихідний стан для повторення циклу, то ніякої корисної роботи такий двигун не передасть. . Формулювання Томсона, Томсона — Планка, а також Вільгельма Оствальда по суті зводяться до твердження про неможливість створення вічного двигуна другого роду, тобто безперервно (циклічно) діючої ізотермічної теплової машини, здатної працювати від одного теплового джерела (наприклад, океану) і, таким чином, перетворювати всю енергію, витянуту з довкілля, що має постійну температуру, в роботу. , , . Існують докази еквівалентності формулювань Клаузіуса та Томсона — Планка. . Проте, еквівалентність формулювань не є повною. Формулювання Клаузіуса відрізняється від формулювань Томсона та Планка тим, що воно не пов'язане з роботою теплових двигунів (циклом). Тому формулювання Клаузіуса має більший ступінь спільності. Узагальнюючи формулювання Томсона — Планка на будь-які системи можна виразити його так:

Неможливо збільшити нерівноважність будь-якої системи (перевести її з більш рівноважного стану до менш рівноважного) без компенсації .

4. Формулювання Планка (1926 р.) (Постулат М. Планка)

Утворення тепла шляхом тертя незворотне.

Постулат М. Планка дуже лаконічний, але все ж таки в ньому, поряд з категоричним запереченням можливості повного перетворення тепла в роботу, міститься і вказівка ​​про можливість повного перетворення роботи в тепло шляхом тертя.

Цикл і теорема Карно

Теплові машини, до яких у термодинаміці відносяться теплові двигуни, холодильні машини та теплові насоси, для забезпечення безперервної роботи повинні працювати по замкнутому колу (циклу), при якому робоче тіло теплової машини періодично повертається у вихідний стан. Одним із ідеалізованих циклів теплової машини є цикл, запропонований Саді Карно для аналізу роботи теплових машин з метою підвищення ефективності їх роботи.

Мал. 1. Цикл Карно в координатах P і V

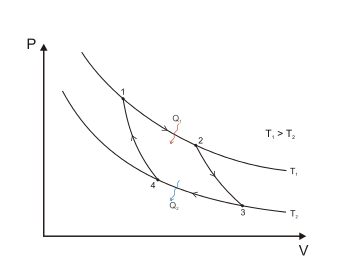
На діаграмі 1 представлений зворотний цикл Карно, здійснений між двома джерелами тепла постійної температури. Він складається з двох звооротних ізотермічних (1-2 і 3-4) та двох зворотних адіабатних (2-3 і 4-1) процесів. Робочим тілом цієї термічної машини є ідеальний газ. (Основна стаття: Цикл Карно). Теорема Карно стверджує, що термічний ККД зворотного циклу Карно не залежить від природи робочого тіла і визначається лише температурами нагрівача $T_{1}$ та холодильника $T_{2}$:

$$\eta ={\frac {T_{1}-T_{2}}{T_{1}}}=1-{\frac {T_{2}}{T_{1}}}$$

Досвід показує, що механічну, електричну роботу, роботу магнітних сил, і так далі можна повністю, без залишку, перетворити на тепло шляхом тертя або електронагріву. Що ж до тепла, то тільки частина його може бути перетворена на роботу в циклічно працюючему тепловому двигуні. Інша його частина неминуче має бути передана холодному джерелу. Ряд авторів приписують цей факт особливим властивостям тепла. Наприклад, за твердженням І. П. Базарова: З визначення понять теплоти і роботи слід, що дві форми передачі енергії, що розглядаються в термодинаміці, не є рівноцінними: у той час як робота $W$ може безпосередньо піти на збільшення будь-якого виду енергії і повністю, шляхом тертя, перетворитися на тепло, то тепло $Q$ безпосередньо, призводить лише до збільшення внутрішньої енергії системи. Доказ нерівноцінності тепла і роботи автор ґрунтує на тому, що кількість тепла $Q$, яке підводиться до двигуна, завжди більше роботи $W$, що відводиться від нього, а в процесі тертя витрачена робота дорівнює теплу тертя. На хибність цього доказу вказав В. В. Риндін. За його словами, у доказі порівнюються різні поняття: цикл (при перетворенні тепла на роботу) та окремий процес — перетворення роботи в тепло. . Неправомірність доказу, продовжує В. Риндін, обумовлена ​​ще й тим, що порівнюються не лише різні поняття — цикл і процес, а й різні процеси: природні та протиприродні. При здійсненні циклу за рахунок тепла виконується робота — протиприродний процес, що віддаляє систему гаряче тіло — робоче тіло, від стану рівноваги. Такий процес вимагає компенсації, тобто зменшення термічної нерівноважності в системі гаряче тіло — холодне тіло. Це здійснюється в результаті відведення частини тепла від гарячого тіла до холодного. (Іншої компенсації в циклі немає, оскільки робоче тіло свій стан не змінює).

Інтеграл Клаузіуса і термодинамічна ентропія

Із зіставлення рівняння ККД зворотного циклу Карно

$$\eta ={\frac {T_{1}-T_{2}}{T_{1}}}=1-{\frac {T_{2}}{T_{1}}}$$

і рівняння ККД будь-якого циклу

$$\eta ={\frac {Q_{1}-Q_{2}}{Q_{1}}}$$

слідує співвідношення

$${\frac {Q_{1}}{T_{1}}}={\frac {Q_{2}}{T_{2}}},$$

звідки, з урахуванням прийнятої системи знаків: плюс ─ для тепла, що підводиться, і мінус ─ для тепла, що відводиться, отримаємо

$${\frac {Q_{1}}{T_{1}}}+{\frac {Q_{2}}{T_{2}}}=0$$

або

$$\sum {\frac {Q}{T}}=0.$$

Відношення ${\frac {Q}{T}}$ називається приведеною теплотою, а алгебраїчна сума приведених теплот для зворотного циклу Карно дорівнює нулю. Далі Клаузіус, розбиває адіабатами довільний зворотний цикл, на нескінченно велике число елементарних циклів Карно і виводить рівняння

$$\lim _{n\rightarrow \infty }\sum _{n=1}^{\infty }{\frac {Q_{n}}{T_{n}}}=0.$$

Ввівши позначення

$$\oint {\frac {\delta Q}{T}}\equiv \lim _{n\rightarrow \infty }\sum _{n=1}^{\infty }{\frac {Q_{n}}{T_{n}}},$$

отримуємо:

$$\oint {\frac {\delta Q}{T}}=0.$$

Цей вираз називається інтегралом або рівнянням Клаузіуса. Іноді його називають першим інтегралом Клаузіуса. Оскільки при зворотному процесі інтеграл Клаузіуса, узятий по контуру циклу, дорівнює нулю, то його значення не залежить від шляху процесу, а визначається лише початковим і кінцевим станом тіла. Це означає, що підінтегральний вираз є повний диференціал деякої функції $(S)$ стану тіла (системи), яку Клаузіус назвав ентропією, точніше — термодинамічною або тепловою ентропією . (Далі, якщо не обумовлено особливо, під ентропією матимется на увазі термодинамічна ентропія). Для нескінченно малого зворотного процесу

$$dS_{\text{звор}}={\frac {\delta Q_{\text{звор}}^{*}}{T}},$$

звідки

$$\delta Q_{\text{звор}}^{*}=TdS_{\text{звор}}$$

Оскільки елементарна кількість тепла $\delta Q$ не є повним диференціалом, а $dS$ є повний диференціал, то абсолютна температура $T$ виступає тут як інтегруючий дільник, який перетворює неповний диференціал $\delta Q$ у повний. Вираження $\delta Q_{\text{звор}}^{*}=TdS_{\text{звор}}$ є математичним вираженням другого закону термодинаміки для зворотних процесів або принципом існування термодинамічною ентропії. .

Розглянемо незворотний процес, поданий на мал. 2

Мал.2 Незворотний процес

Він складається з двох гілок: незворотного процесу AIB і зворотного BIIA, за допомогою якого тіло повертається у вихідний стан. Цикл AIBIIA — незворотний через незворотність процесу AIB. Перший інтеграл Клаузіуса можна записати у вигляді

$$\oint {\frac {\delta Q}{T}}=\int _{AIB}{\frac {\delta Q}{T}}-\int _{BIIA}{\frac {\delta Q}{T}}<0$$

Другий інтеграл, взятий по зворотній ділянці AIIB, є різницею $\Delta S$ ентропій між точками A і B. Звідси випливає, що для будь-якого незворотного процесу в будь-якій системі

$$\int _{A}^{B}{\frac {\delta Q}{T}}<\Delta S$$

Цей вираз отримав назву другий інтеграл або нерівність Клаузіуса.

У диференціальному вигляді:

$$dS>{\frac {\delta Q}{T}}$$

Отже, в ізольованій системі, де $\delta Q^{*}=0$ (1)

$dS>0$ (2),

тобто, у всіх незворотних процесах ентропія ізольованої системи незмінно зростає.

(Зростання ентропії в рівноважних процесах та адіабатних системах пов'язане з умовою, що визначає додатковість термодинамічної температури. За іншою додатковою умовою, що призводить до від'ємних термодинамічних температур для нерівноважних процесів у звичайних адіабатно ізольованих системах, ми мали б закон убування.

Вираз $dS>0$ є принцип зростання ентропії ізольованих систем або математичний вираз другого закону термодинаміки для нерівноважних процесів. .

Загальний математичний вираз другого закону термодинаміки

Другий закон класичної термодинаміки формулюється як об'єднаний принцип існування та зростання ентропії ізольованих систем. З рівняння (1) та нерівності (2) :

$$dS={\frac {\delta Q^{*}}{T}}\geq 0.$$

Статистичне визначення ентропії

Людвіг Больцман у роботі «Про зв'язок між другим законом механічної теорії теплоти і теорією імовірностей у теоремах про теплову рівновагу» показав зв'язок між ентропією та статистичною вагою (термодинамічною імовірністю) макростану фізичної системи. Закон зростання ентропії у Больцмана отримав просту статистичну інтерпретацію: система прагне найімовірнішого стану; мимовільно протікають ті процеси, у яких система з менш імовірного стану перетворюється на більш імовірний. Запропонована Больцманом інтерпретація ентропії як міри впорядкованості/невпорядкованості на атомно-молекулярному рівні дозволила виявити низку важливих закономірностей, які стають очевидними, якщо замінити термін ентропія словом невпорядкованість.

У статистичній фізиці ентропія $(S)$ системи розглядається як функція імовірності $(W)$ її стану (принцип Больцмана).

$$S=k\ln W,$$

де $k$ ─ стала Больцмана, $W$ ─ термодинамічна імовірність стану, яка визначається кількістю мікростанів, що реалізовують цей макростан.

Тут слід зробити важливе зауваження. За час, що минув із запровадження поняття ентропія зміст, що вкладувався у принцип зростання ентропії зазнав істотну зміну. Якщо спочатку поняття ентропія відносилося виключно до теплових процесів, то надалі його стали узагальнювати в інші, нетеплові процеси, зокрема, у статистичну ентропію Больцмана і Гіббса і статистичну ентропію як (макро)імовірність стану. Стосовно такого розширеного поняття ентропії закон її зростання набуває форми закону зростання повної ентропії, то слід визнати закон зростання теплової ентропії недіючим і, як наслідок, визнати заборону на вічні двигуни другого роду недійсною. .

Фізичний сенс термодинамічної ентропії

Серед величин, що визначають стан термодинамічної системи, ентропія займає особливе положення. Виходячи з математичного трактування термодинамічної ентропії, даної Клаузіусом, $\delta Q_{\text{звор}}^{*}=TdS_{\text{звор}}$ випливає, що теплота будь-якого нескінченно малого квазістатичного процесу дорівнює добутку диференціалу ентропії на термодинамічну температуру. Поняття ентропія, як було зазначено в преамбулі, відрізняється своєю абстрактністю, фізичний сенс ентропії безпосередньо не випливає з її математичного вираження і не піддається простому інтуїтивному сприйняттю. У зв'язку з цим неодноразово робилися спроби усвідомити фізичне значення ентропії. Одна із спроб була заснована на пошуку аналогій ентропії з більш доступними для сприйняття поняттями. Наприклад, якщо елементарна робота є добутком сили на елементарне переміщення, то аналогом роботи може бути кількість тепла, аналогом сили — абсолютна температура, а аналогом переміщення — ентропія. Очевидно, що аналогії подібного типу мають штучний характер, і користь від них для інтерпретації ентропії є дуже сумнівною. Також неспроможною є спроба проведення аналогії ентропії з теплоємністю.

Порівняємо вираз для питомої ентропії тіла:

$ds={\frac {\delta q}{T}}$

з вираженням питомої теплоємності:

$c={\frac {\delta q}{dT}}$.

Подібність цих виразів полягає у використанні однакових величин і в однаковій розмірності теплоємності та ентропії. Обидві величини є кількість тепла, віднесена до одиниці маси та одиниці температури. Однак, якщо у формулі теплоємності температура входить у диференціальній формі і її можна вимірювати у будь-якій температурній шкалі, то у формулі ентропії фігурує абсолютна температура $T$. На відміну від ентропії, теплоємність не є функцією стану системи, тому що $\delta Q$ не є повним диференціалом, а є функцією процесу, оскільки залежить від способу передачі тепла (наприклад, при постійному тиску або постійному обє'му і так далі). Ентропія є функцією стану термодинамічної системи і її значення не залежить від зміни системи поблизу заданого стану. Отже, теплоємність є величиною змінною, а ентропія — статичною. Фізичний зміст ентропії може бути виражений таким чином:

Ентропія (віднесена до одиниці маси) є питома кількість тепла, необхідного для того, щоб після адіабатичного та зворотного процесу, що завершується при температурі, яка відповідає початковому стану, повернути робоче тіло зворотним шляхом у цей початковий стан. (Умова зворотності показує, що йдеться про мінімальну питому кількість тепла).

Звідси можна дійти до висновку, що цінність переданого тепла тим вище, чим вище температура, при якій ця передача відбувається. Передача робочому тілу кількості тепла $\delta Q$ при температурі $T$ означає збільшення ентропії на величину переданого тепла $\delta Q$, необхідного для повернення робочого тіла в початковий стан. Але ця кількість тепла при заданому $\delta Q$ буде тим меншою, чим вища температура $T$. Звідси випливає, що при зростанні температури $T$ зменшується величина $\delta Q_{0}$ і, отже, кількість тепла, що перетворюється на роботу, тобто $\delta Q-\delta Q_{0}$ збільшується, що, у свою чергу, проясняє фізичний сенс ентропії як міри оцінки якості тепла у плані його придатності до перетворення на роботу. . З фізичною і філософською точок зору термодинамічна ентропія характеризує також міру нерівноважності, незворотності, неідеальності реального термодинамічного процесу. Подібно до того, як енергія є фізичною величиною, яка є кількісною характеристикою руху, так і ентропія (точніше зміна ентропії) може бути визначена як фізична величина, що є кількісною характеристикою зміни деякої властивості матерії — нерівноважності термодинамічного процесу.

Ревізія постулатної бази і проблема обґрунтування другого закону термодинаміки

Класичні формулювання другого закону і метод його обґрунтування визначилися ходом історичного розвитку термодинаміки. На перших порах вчені не замислювалися над тим, чи є в логічному відношенні другий закон термодинаміки настільки ж бездоганним, як і перший закон, що є окремим випадком загального закону збереження і перетворення енергії, спільність і універсальність якого майже ні в кого не викликала сумнівів вже в кінці 70-х років XIX століття. Зрозумілим було бажання вчених бачити настільки ж фундаментально обґрунтованим і другий закон термодинаміки, спільність якого також була досить очевидна.

На рубежі XIX ─ XX століть термодинаміка вийшла за межі взаємозв'язку тепла і роботи і взагалі за рамки фізики. Стало ясно, що обидва закони термодинаміки, на яких заснований термодинамічний метод, являють собою найбільш загальні закони природи. Нові теорії і погляди в області фізики, хімії та біології повинні бути узгоджені не тільки з першим, але і з другим законом термодинаміки. Виникла потреба в строгому універсальному термодинамічному методі феноменологічного опису природних явищ в різних областях природознавства, не прив'язаному до конкретних технічних рішень, технологічних процесів, гіпотез і теорій про будову речовини. До формулювань і обґрунтувань другого закону термодинаміки до цього часу накопичилося чимало зауважень:

1. Вперше Герман Гельмгольц (1884) звернув увагу на ту обставину, що для визначення ентропії і абсолютної термодинамічної температури немає необхідності розглядати кругові процеси і залучати гіпотезу про існування ідеального газу, оскільки абсолютна температура будь-якого тіла є не що інше, як той інтегруючий дільник для елементарної кількості тепла, який залежить від однієї тільки температури тіла, відрахованої в довільно обраній шкалі.

2. Постулати Клаузіуса і Томсона формулюються як заперечення можливості будь-якого явища, тобто як постулати заборони. Вони абсолютно не відповідають сучасним вимогам, що пред'являються до обґрунтування другого закону термодинаміки як принципу існування ентропії, і не цілком задовольняють задачі обґрунтування принципу зростання ентропії, тому що вони повинні містити пряму вказівку про певну спрямованість спостережуваних в природі незворотних явищ, а не заперечення можливості протилежної їх течії. Справа в тому, що заперечення можливості протікання процесу переходу тепла від більш холодного тіла до більш теплого зовсім не означає можливість його переходу від більш теплого тіла до більш холодного, тобто заперечення можливості будь-якої нерівності $x\not \geq N$ нееквівалентно твердженню необхідності нерівності протилежного знака $x<N$..

3. Класичні формулювання другого закону термодинаміки і метод його обґрунтування визначилися ходом історичного розвитку термодинаміки. Вони з самого початку об'єднували два різнорідних принципи: принцип існування і принцип зростання ентропії, причому вирішальну роль в обґрунтуванні другого закону грав принцип зростання ентропії ─ постулат незворотності .

4. У побудові другого закону класичної термодинаміки як об'єднаного принципу існування і зростання ентропії використовувався метод кругових процесів, теоретично розвинений Карно, а потім широко використаний Клаузіусом і іншими вченими. Це неминуче призводить до обмежених виразів принципу існування ентропії, дійсним лише для зворотних процесів:

$$dS_{\text{звор}}={\frac {\delta Q_{\text{звор}}^{*}}{T}}$$.

5. Обґрунтування теореми Карно, запропоноване Р. Клаузіусом, що набуло широкого поширення, не може, бути визнано правильним, оскільки в схему доказу теореми Карно внесено зайву умову: більш досконалій, за припущенням, зворотній машині в схемі механічно пов'язаних зворотних машин незмінно приписується роль теплового двигуна, що в поєднанні з постулатом односторонньої заборони про неможливість мимовільного переходу тепла від тіл менш нагрітих до більш нагрітим призводить до правильного вираження теореми Карно. Однак, якщо в схемі побудов Клаузіуса найгіршу (за припущенням) зворотну машину розглядати як двигун, то для доведення теореми Карно необхідно ввести постулат, протилежний постулату Клаузіуса . До такого ж висновку прийшов і А. А. Гухман. Він довів теорему Карно, замінивши постулат Клаузіуса антипостулатом. Заміна постулату Клаузіуса (вихідної передумови) його антитезою не відбивається ні на суті одержуваних результатів, ні на способі їх отримання, що повністю збігається з твердженням Білоконя. В кінцевому рахунку Гухман приходить до висновку, що запропонований Клаузіусом доказ теореми Карно в дійсності не заснований на його постулаті .

6. При побудові принципу існування ентропії р. Клаузіус поширює вирази ККД зворотного циклу Карно для ідеальних газів на всі зворотні цикли теплових машин, неявно включаючи в схему висновків постулат про можливість існування ідеальних газів, що підкоряються як рівнянню Клапейрона $PV=RT$, так і закону Джоуля $u=u(t)$. Обґрунтування принципу існування абсолютної температури і ентропії, що має досить загальний характер, на базі такого сумнівного постулату, як твердження про можливість існування ідеальних газів, не можна вважати переконливим, оскільки, твердження про можливість існування ідеальних газів, не є безпосередньо очевидним, а дослідження фізичного стану реальних тіл не дають підстав, для тверджень про існування газоподібних станів, що задовольняють при всіх значеннях густини законам Бойля і Джоуля.

7. Твердження статистичної фізики про імовірнісний характер принципу незворотності і відкриття в 1951 р. незвичайних (квантових) систем з від'ємними абсолютними температурами, похитнули базові постулати Клаузіуса, Томсона (Кельвіна) і Планка, повністю відкинувши одні, або наклавши серйозні обмеження на інші.

Незадоволеність вчених існуючими методами обґрунтування другого закону і їх логічною неспроможністю стала стимулом розвитку аксіоматичного напрямку в термодинаміці. Справжньою ж причиною цієї незадоволеності послужив той факт, що до 80-х років XIX ст. виникла потреба в термодинамічному методі, вільному від необхідності введення припущень про механізми процесів, гіпотез, що вимагають подальшої дослідної перевірки, зокрема, гіпотез і теорій про будову речовини. Цей метод повинен бути досить загальним, універсальним методом феноменологічного опису явищ природи, який можна було б використовувати і в інших галузях теоретичного природознавства. Стало ясно і те, що обидва закони термодинаміки, які засновані на цьому методі, являють собою найбільш загальні закони природи.

Аксіоматичний напрямок в обґрунтуванні другого закону термодинаміки

У XX столітті завдяки роботам М. Шиллера, К. Каратеодорі, т. Афанасьєвої-Еренфест, А. А. Гухмана, М. І. Білоконя та ін. по обґрунтуванню другого закону термодинаміки з'явився новий, аксіоматичний напрямок. З'ясувалося, що принцип існування ентропії може бути обґгрунтований незалежно від напрямку спостережуваних в природі мимовільних процесів, а для визначення абсолютної температури і ентропії не потрібно ні розгляду кругових процесів, ні припущень про існування ідеальних газів. . Автори аксіоматичного напряму обрали дедуктивний шлях, заснований на допущенні деякого числа досить абстрактних і більш-менш імовірних аксіом, обґрунтованих з експериментальної та логічної сторони і не пов'язаних з конкретними, наприклад, тепловими процесами.

Метод Шиллера-Каратеодорі

У 1909 р. великий німецький математик грецького походження Костянтин Каратеодорі, а ще раніше М. Шиллер обґрунтували принцип існування абсолютної температури та ентропії на основі дослідження теплової рівноваги тіл. Ця ідея отримала розвиток у роботах К. Каратеодорі. Постулат Каратеодорі був висунутий не шляхом дослідження станів реальних термодинамічних систем, а на основі математичного розгляду виразів зворотного теплообміну як диференціальних поліномів (форм Пфаффа). Метод Шиллера — Каратеодорі не набув широкого поширення у зв'язку з недостатньою наочністю вихідних передумов і деякими особливостями математичного оформлення висновків. В основу методу був покладений постулат Каратеодорі:

У будь-якій околиці довільно заданого початкового стану системи є стани, які недосяжні довільною адіабатичною зміною стану.

Ця аксіома отримала надалі в термодинамічній літературі найменування принципу адіабатичної недосяжності. Згідно з твердженням Каратеодорі, якщо диференціальний поліном Пфаффа $\sum X_{i}dx_{i}$ має ту властивість, що в довільній близькості деякої точки існують інші точки, недосяжні за допомогою послідовних переміщень шляхом $\sum X_{i}dx_{i}=0$, то існують інтегруючі дільники цього полінома і рівняння $\sum X_{i}dx_{i}=0$. (Теорема Каратеодорі).

Основні недоліки методу Шиллера — Каратеодорі:

1. Відсутня безпосередня очевидність у твердженні Шиллера про існування інтегруючих дільників виразів зворотного теплообміну системи тіл, що знаходяться у стані теплової рівноваги.

2. При переході від постулатів Шиллера до твердження про існування інтегруючих дільників виразів зворотного теплообміну неявно використані передумови, еквівалентні теоремі Каратеодорі, які не є очевидними.

3. За словами Білоконя "… Постулати М. Шиллера (|—|||), навіть після внесення необхідних коректив, не можуть бути віднесені до категорії безпосередньо очевидних положень, причому загальний доказ цих положень можливий лише на основі принципу існування ентропії, у зв'язку з чим виключається можливість плідного використання постулатів М. Шиллера як засобів обґрунтування цього принципу."

4.Шиллер неявно використовував безпосередньо неочевидну передумову існування адитивних $S$ функцій.

Критично до постулату Каратеодорі відносився М. Планк. З його точки зору "висловлювання, що міститься в ньому, не є загальнозастосовним до природних процесів … "Ніхто ще й ніколи не ставив дослідів з метою досягнення всіх суміжних станів якогось певного стану адіабатичним шляхом" . Системі Каратеодорі Планк протиставляє свою систему, засновану на постулаті: Утворення теплоти за допомогою тертя незворотне, яким, на його думку, вичерпується зміст другого закону термодинаміки. Тим часом метод Каратеодорі отримав високу оцінку в роботі Т. Афанасьєвої-Еренфест «Незворотність, однобічність і другий закон термодинаміки» (1928 р.). У своїй чудовій статті Т. Афанасьєва-Еренфест дійшла до ряду найважливіших висновків, зокрема:

1. Основний зміст другого закону полягає в тому, що елементарна кількість тепла $\delta Q$, яким система обмінюється в квазістатичному процесі, може бути представлена у вигляді $TdS$, де $T=f(t)$ ─ універсальна функція температури, яка називається абсолютною температурою, а $(S)$ ─ функція параметрів стану системи, що отримала назву ентропії. Саме вираз $\delta Q=TdS$ є принцип існування ентропії.

2. Принципова відмінність нерівноважних процесів від рівноважних полягає в тому, що в умовах неоднорідності температурного поля всередині термодинамічної системи, а також втрат роботи в незворотних процесах на тертя, опір, можливий перехід системи до стану з іншою ентропією без обміну теплотою з довкіллям. (Цей процес пізніше у працях М. І. Білоконя отримав назву внутрішнього теплообміну або теплообміну робочого тіла. Внутрішній теплообмін в ізольованій системі завжди незворотний і наслідком його є односторонність процесу .

3. Одностороння зміна ентропії однаково мислима як неухильне її зростання або як неухильне спадання. Фізичні передумови, такі як адіабатична недосяжність та незворотність реальних процесів, не виражають жодних вимог щодо переважного напряму течії мимовільних процесів.

4. Щоб узгодити отримані висновки з дослідними даними для реальних процесів необхідно прийняти постулат, сфера дії якого визначається межами застосовності цих даних. Таким постулатом є принцип зростання ентропії.

А. А. Гухман, оцінюючи роботу Каратеодорі, вважає, що вона відрізняється формальною логічною строгістю і бездоганністю в математичному відношенні… разом з тим, в прагненні до найбільшої спільності Каратеодорі надав своїй системі настільки абстрактну і складну форму, що вона виявилася фактично недоступною для більшості фізиків того часу. Щодо постулату адіабатичної недосяжності Гухман зауважує, що він, як фізичний принцип, не може бути покладений в основу теорії, що має універсальне значення, оскільки не володіє властивістю самоочевидності. "Все гранично ясно щодо простої … системи … але ця ясність повністю втрачається в загальному випадку гетерогенної системи, ускладненої хімічними перетвореннями і впливом зовнішніх полів." . Він також говорить і про те, наскільки права була Афанасьєва-Еренфест, наполягаючи на необхідності повного відділення проблеми існування ентропії, від усього, що пов'язано з ідеєю незворотності реальних процесів . Щодо побудови основ термодинаміки Гухман вважає, що "самостійної окремої проблеми існування ентропії немає. Питання зводиться до поширення на випадок термічної взаємодії досвіду вивчення всіх інших енергетичних взаємодій, що завершуються встановленням однакового за формою рівняння для елементарної кількості впливу $dQ=Pdx$ ця екстраполяція дає підстави прийняти її в якості правдоподібної гіпотези і тим самим постулювати існування ентропії. Слід однак зауважити, що постулювання принципу існування ентропії на підставі загальнолюдського досвіду істотно обмежує сферу його дії як фундаментального закону природи.

М. І. Білоконь у своїй монографії «Термодинаміка» дав детальний аналіз чисельних спроб обґрунтування другого закону термодинаміки як об'єднаного принципу існування та зростання ентропії на основі одного лише постулату незворотності. Він показав, що спроби такого обґрунтування не можуть бути виправдані, по-перше, тому, що висновок про існування ентропії та абсолютної температури не має жодного відношення до незворотності явищ природи, оскільки ці функції існують незалежно від зростання або спадання ентропії ізольованих систем. По-друге, вказівка про напрямок незворотних явищ, що спостерігаються, знижує рівень спільності другого закону термодинаміки і, по-третє, використання постулату Томсона — Планка про неможливість повного перетворення тепла в роботу суперечить результатам досліджень систем з від'ємною абсолютною температурою, в яких може бути здійснено повне перетворення тепла роботу, але неможливе повне перетворення роботи на тепло. Слідом за Т. Афанасьєвою-Еренфест М. І. Білоконь стверджує, що відмінність змісту, рівня спільності та сфери застосування принципів існування і зростання ентропії цілком очевидна з наступних причин:

1. З принципу існування ентропії випливає ряд найважливіших диференціальних рівнянь термодинаміки. Його наукове і практичне значення важко переоцінити.

2. Принцип зростання ентропії ізольованих систем є твердження про незворотність течії спостережуваних в природі явищ. Цей принцип використовується в судженнях про найбільш імовірний напрям течії фізичних і хімічних процесів і з нього випливають всі нерівності термодинаміки.

У. І. Франкфурт у своїй статті "До історії аксіоматики термодинаміки", яка опублікована у збірнику "Развитие современной физики" (1964г.), зазначає, що в останні роки з'явилися заперечення проти одного з основних постулатів Шиллера, який проголошує, що у зворотному адіабатичному процесі зміни стану тіла, що характеризується за допомогою незалежних один від одного параметрів, будь-який із згаданих параметрів повертається до свого первісного значення, коли $\ n-1$ параметрів повертається до своїх. Далі, продовжує Франкфурт, посилаючись на Білоконя, "в такому загальному формулюванні основний постулат М. М. Шиллера не може бути визнаний справедливим… Якщо доповнити основний постулат Шиллера зазначенням, що всі частини тіла, що змінюється (або системи) знаходяться в тепловій рівновазі, то цей постулат може розглядатися як окремий вираз теплової рівноваги тіл…" , . Щодо обґрунтування принципу існування ентропії за методом Шиллера ─ Каратеодорі Білоконь зазначає, що в побудовах за цим методом абсолютно обов'язковим є використання теореми Каратеодорі про умови існування інтегруючих дільників диференціальних поліномів $\delta Q=\sum X_{i}dx_{i}=\tau dZ$, однак, необхідність використання цієї теореми "повинна бути визнана дуже сором'язливою, оскільки загальна теорія диференціальних поліномів розглянутого типу (форм Пфаффа) представляє відомі труднощі і викладається лише в спеціальних працях з вищої математики." У більшості курсів термодинаміки теорема Каратеодорі дається без доказу, або наводиться доказ у нестрогому, спрощеному вигляді .

Аналізуючи побудову принципу існування ентропії рівноважних систем за схемою К. Каратеодорі, М. І. Білоконь звертає увагу на використання необґрунтованого припущення про можливість одночасного включення температури $t$ та $Z$ ─ функції до складу незалежних змінних станів рівноважної системи і приходить до висновку, що постулат Каратеодорі, еквівалентний групі загальних умов існування інтегруючих дільників диференціальних поліномів $\sum X_{i}dx_{i}$, є недостатнім для встановлення існування первинного інтегруючого дільника $\tau (t)=T$, тобто для обґрунтування принципу існування абсолютної температури та ентропії. Далі він стверджує, що при побудові принципу існування абсолютної температури та ентропії на основі теореми Каратеодорі повинен бути використаний такий постулат, який був би еквівалентним теоремі про несумісність адіабати та ізотерми. У цих коригованих побудовах стає зовсім зайвим постулат Каратеодорі, оскільки він є окремим випадком необхідної теореми про несумісність адіабати та ізотерми .

Метод М. І. Білоконя

За цим методом другий закон термодинаміки поділено на два незалежні принципи:

1. Принцип існування абсолютної температури та ентропії —Другий закон термостатики.

2. Принцип зростання ентропії — Другий закон термодинаміки .

Кожен із цих принципів отримав самостійне обґрунтування на підставі незалежних постулатів.

• Постулат другого закону термостатики (Білоконя):

Температура є єдина функція стану, що визначає напрямок мимовільного теплообміну, тобто між тілами і елементами тіл, що не знаходяться в тепловій рівновазі, неможливий одночасний мимовільний (по балансу) перехід тепла в протилежних напрямках — від тіл більше нагрітих до тіл менш нагрітих і навпаки. .

Постулат Білоконя самоочевидний, оскільки є окремим вираженням причинного зв'язку і однозначності законів природи. Наприклад, якщо існує причина, в силу якої в цій системі тепло переходить від більш нагрітого тіла до менш нагрітого, то ця причина в тих же умовах перешкоджатиме переходу тепла у протилежному напрямку, і навпаки. Цей постулат є повністю симетричним відносно напрямку незворотних процесів, оскільки не містить ніяких вказівок про спостережуваний напрямок незворотних явищ у світі додатних абсолютних температур.

• Слідства другого закону термостатики:

Слідство I. Неможливе одночасне (у рамках однієї і тієї ж просторово-часової системи додатних або від'ємних абсолютних температур) здійснення повних перетворень тепла в роботу і роботи в тепло.

Слідство II. (теорема несумісності адіабати і ізотерми):

На ізотермі рівноважної термодинамічної системи, що перетинає дві різні адіабати тієї ж системи, теплообмін не може дорівнювати нулю.

Слідство III (теорема теплової рівноваги тіл):

У рівноважних кругових процесах двох термічно зв'язаних тіл $(t_{I}=t_{I}I)$, що утворюють адіабатично ізольовану систему, обидва тіла повертаються на вихідні адіабати і в початковий стан одночасно..

На підставі слідств постулату другого закону термостатики М. І. Білоконь запропонував схеми побудови принципу існування абсолютної температури та ентропії для зворотних і незворотних процесів $\delta Q=\delta Q^{*}+Q^{**}TdS$ .

• Постулат другого закону термодинаміки:

Робота може бути безпосередньо і повністю перетворена на тепло шляхом тертя або електронагріву.

Слідство I.Тепло не може бути повністю перетворено на роботу (принцип виключеного Perpetuum mobile II роду):

$$\eta <1$$.

Слідство ІІ. ККД або холодопродуктивність будь-якої незворотної теплової машини при заданих температурах зовнішніх джерел завжди менша за ККД або холодопродуктивності зворотних машин, що працюють між тими ж джерелами.

Зниження ККД та холодопродуктивності реальних теплових машин пов'язане з нерівноважним теплообміном через різницю температур джерела тепла і робочого тіла та за рахунок незворотних втрат роботи на тертя і внутрішні опори. Зі слідства I другого закону термостатики і слідства II другого закону термодинаміки безпосередньо випливає неможливість здійснення Perpetuum mobile I та II роду. Говорячи про ступінь спільності постулатів і відповідних принципів термодинаміки, Білоконь зазначає, що перший постулат — закон збереження енергії, який є основою першого закону термодинаміки, дійсний в умовах будь-яких процесів, що протікають у природі; другий постулат (Білоконя), що є основою другого закону термостатики, може розглядатися як окремий вираз принципу причинного зв'язку явищ природи, і його рівень спільності дещо знижується в порівнянні з першим постулатом додатковим зазначенням взаємозв'язку понять тепло і температура; третій постулат, який є основою другого закону термодинаміки, (принцип зростання'ентропії) має статистичний характер і розглядається як твердження про найбільш імовірний напрямок течії природних процесів, що безпосередньо спостерігаються. .

Другий закон термодинаміки для систем з від'ємними абсолютними температурами

На перший погляд твердження термодинамічна система з від'ємними абсолютними температурами виглядає абсурдним, тому що суперечить визначенню поняття температура, що прийняте в загальних курсах фізики та в класичній рівноважній термодинаміці. Дійсно, згідно з другим законом термодинаміки, відношення абсолютних температур ${T_{1}}$ , ${T_{2}}$ двох станів термодинамічної системи виражається показниковою функцією

${\frac {T_{1}}{T_{2}}}=e^{I}$

Звідси нібито робився висновок, що термодинамічна температура не може змінювати знак, тобто бути завжди додатною, або завжди від'ємною. Насправді це відноситься до квазістатичних (рівноважних) переходів з одного рівноважного стану до іншого для звичайних систем з додатними абсолютними температурами, але не відноситься до переходів з одного стану до іншого нестатичним шляхом. Висновок про те, що абсолютна температура не може змінювати знак, тобто бути або завжди додатною, або від'ємною не випливає з наведеного вище виразу без додаткової заборони на можливість існування поряд з додатними — від'ємних абсолютних температур. Такий висновок буде справедливим, якщо до нього приєднується твердження, що стани, які можна досягти з даного стану нерівноважним шляхом, завжди досяжні з нього і шляхом рівноважним. Це твердження є вірним для звичайних систем, що найчастіше зустрічаються. Для них термодинамічна температура не може змінювати свій знак. Вона може бути або додатною або від'ємною. Можливість існування від'ємних температур не суперечить також слідству третього закону термодинаміки про недосяжність абсолютного нуля ($0K$). Це твердження забороняє лише перехід через нього з області додатних температур в область температур від'ємних.

З молекулярно-кінетичної точки зору температура визначається як фізична величина, що характеризує інтенсивність хаотичного (теплового) руху всієї сукупності частинок системи і яка пропорційна до середньої кінетичної енергії поступального руху однієї частки. Згідно співідношенню Максвелла температура визначається рівнянням

$T=\left({\frac {\partial U}{\partial S}}\right)$_v

З цього рівняння випливає, що в міру збільшення температури при підведенні енергії, все більше частинок переходить на верхні енергетичні рівні і, відповідно, посилюється безлад системи, тому що частки щоразу розподіляються за більшим числом рівнів. При зростанні енергії та ентропії, оскільки $\Delta U$ і $\Delta S$ додатні, то і їхнє відношення також буде додатним. З формули Максвелла також випливає, що для того, щоб при збільшенні енергії системи температура була від'ємною, потрібно зменшення ентропії системи.

Крім молекулярно-кінетичного визначення температури як величини, що характерізує інтенсивність руху частинок, температура є величиною, що визначає розподіл частинок за енергетичними рівнями (формула Больцмана):

${\frac {n}{n_{0}}}=e^{\frac {-U}{kT}}$,

де $n_{0}$ і $n$ — число частинок на вихідному рівні й на рівні $U$.

При рівноважному стані системи і додатних значень температури $(T)$ $n$ завжди менше, ніж $n_{0}$. Але, якщо реалізувати систему де $n_{0}<n$, то це означало б, що температура має від'ємне значення. Це означає, що від'ємні температури можуть бути реалізовані не в класичних системах, а тільки в квантових системах із скінченим числом енергетичних рівнів і з врахуваннім того, що ентропія визначає ступінь безладу системи. У такій системі при абсолютному нулі температур усі частинки будуть займати єдино можливі найнижчі рівні і ентропія дорівнюватиме нулю. Із зростанням температури частинки займатимуть всі вищі енергетичні рівні і настане момент, коли всі рівні будуть заселені рівномірно (${\frac {n}{n_{0}}}=1)$, що означає найбільш можливий безлад системи $S=max$, а температура, відповідно до формули Больцмана, буде ± ∞. Якщо далі підводити енергію в систему, то все більше число частинок буде розташовано тільки на високих енергетичних рівнях і, в порівнянні з $S=max$, встановиться більша впорядкованість. Таким чином ентропія системи зменшиться. Відповідно до вище наведених формул Максвелла і Больцмана це означає, що в системі мають місто від'ємні температури. Якщо всі частинки зберуться на вищому рівні, встановиться повна впорядкованість ($S=0$). .

Стани з від'ємними абсолютними температурами не тільки можливі, але й існують насправді. У 1951 році при вивченні ядерних спінів в чистих кристалах фтористого літію (LiF) було виявлено, що при складному впливі сильного магнітного поля або високочастотного імпульсу ядерні спіни орієнтуються в просторі проти поля, тобто таким чином, начебто абсолютна температура була від'ємною величиною. Умови, в яких існують системи з від'ємними температурами, є настільки жорсткими, що вони рідко зустрічаються на практиці, поки тільки в деяких системах ядерних спінів. Від'ємні абсолютні температури досягаються не шляхом відібрання у системи всього тепла, а, навпаки, підводом до системи енергії більше тієї, що відповідає нескінченній температурі. На перший погляд це виглядає абсурдом, оскільки у більшості тіл з ростом температури до нескінченності зростає до нескінченності і внутрішня енергія. Такі системи не можуть перебувати в станах з від'ємними температурами. Але, у деяких систем з ростом температури до нескінченності внутрішня енергія асимптотично наближається до кінцевого (граничного) значенням, і, якщо повідомити цим системам енергію, яка перевищує ту, що відповідає граничному значенню, то це дозволяє отримати стани з від'ємною температурою. Таким чином, при від'ємній температурі система не холодніше, ніж при $+0K$, а більш нагріта, ніж при нескінченній температурі $\infty K$, інакше кажучи, область від'ємних абсолютних температур на температурній шкалі лежить не нижче $0K$, а вище додатних температур. Наприклад, в порядку зростання температура $T$ проходить за шкалою в наступній послідовності:

$+0K,...,+500K,...$, $\pm$$\infty$,... $-500K$, ...,$-0K$.

Удавана безглуздість такої температурної шкали пояснюється випадковим вибором температурної функції. Якби вона була обрана у вигляді ${\frac {-1}{T}}$, то найнижчі температури відповідали б $-\infty$, нескінченні додатні температури ─ нулю, а від'ємні температури відповідали б додатним значенням цієї температурної функції. Таким чином алгебраїчний порядок ходу за шкалою від меншого до більшого був би відновлений. . .

Загальні висновки, які можна зробити про стани з від'ємними абсолютними температурами:

1. Область станів з від'ємними температурами лежить над областю абсолютних додатних температур.

2. Термодинамічні поняття роботи, тепла, більш нагрітого, і менш нагрітого тіла залишаються в силі, наприклад, при $T<0$ більш нагрітим тілом є тіло, що має більш високу від'ємну температуру, тобто меншу за абсолютною величиною.

3. Істотною відмінністю систем з $T<0$ від систем з $T>0$ є те, що в системах від'ємних температур тепло мимовільно повністю переходить в роботу без будь-якої компенсації, а робота перетворюється в тепло тільки з компенсацією.

4. Перший закон термодинаміки як симетричний щодо систем з додатними і від'ємними абсолютними температурами зберігає своє аналітичне вираження. Зберігається також аналітичне вираження другого закону у вигляді

$$dS_{\text{обр}}={\frac {\delta Q_{\text{обр}}^{*}}{T}}.$$

5. Другий закон, сформульований Клаузіусом, зберігає свою силу, оскільки і при $T>0$ і при $T<0$ тепло само собою переходить від більш нагрітого тіла до менш нагрітого, тобто від тіла з більшою температурою до тіла з меншою температурою.

6. Формулювання про неможливість створення вічного двигуна другого роду також зберігає свою силу після внесення в нього уточнення: вічний двигун другого роду неможливий, причому це твердження не допускає звернення в разі звичайних систем з $T>0$ і допускає звернення для незвичайних систем з $T<0$. .

Неможливість звернення твердження про вічний двигун другого роду означає:

Якщо тепло не можна перетворити в роботу повністю без компенсації, то роботу можна перетворити в тепло повністю без всяких компенсацій.

7. Постулат Каратеодорі — принцип адіабатичної недосяжності також зберігає свою силу.

8. Зберігає свою силу і постулат другого закону термостатики (Білоконя), який є симетричним щодо напрямку незворотних процесів, і тому допускає можливість існування систем з від'ємними абсолютними температурами.

9. Формулювання другого закону Томсона ─ Планка перестає бути справедливим при $T<0$, оскільки в області від'ємних абсолютних температур можна здійснити вічний двигун другого роду, який здатний виробляти роботу тільки за рахунок охолодження одного джерела тепла без будь-яких змін в інших тілах. .

10. Ще одна властивість систем з від'ємною температурою полягає в тому, що неможливо зробити зворотний цикл Карно між тілами (системами) з різними знаками, тому що для цього необхідно зворотно пройти через нескінченно великі температури, що нездійснимо. Перехід в стан з від'ємною температурою в дійсності може бути тільки нерівноважним. .

Межі застосування другого закону термодинаміки

У системі ідей Клаузіуса і його послідовників обидва принципи існування і зростання ентропії ґрунтуються на постулаті незворотності (постулати Клаузіуса, Томсона-Кельвіна, Планка та ін.), причому на перше місце поставлений принцип зростання ентропії, який зводиться в ранг універсального закону природи, що стоїть поряд із законом збереження енергії. Абсолютизація Клаузіусом принципу зростання ентропії набула сенсу найважливішого космологічного закону природи, наслідком якого стала антинаукова концепція теплової смерті Всесвіту. Таким чином, будь-яке порушення цього фундаментального закону призвело б до обвалення всіх слідств з нього, що істотно обмежило б сферу впливу термодинаміки. Характерним в цьому сенсі є висловлювання М. Планка, який стверджував, що з незворотністю стоїть і падає термодинаміка. У цьому сенсі висновки статистичної фізики про імовірнісний характер принципу незворотності та відкриття систем з від'ємними абсолютними температурами повинні призвести до краху другого закону, а разом з ним і самої термодинаміки. Однак, цього не сталося. Помилковий висновок М. Планка про "падіння термодинаміки" з падінням постулату незворотності безпосередньо пов'язаний з історично сформованому об'єднанні в одному законі принципів існування і зростання ентропії і надання принципу зростання ентропії сенсу другого закону термодинаміки. На нерівноцінність зазначених принципів і несумісність їх в одному законі термодинаміки звернула увагу Т. Афанасьєва-Еренфест. За її словами, один і той же закон представляється в двох абсолютно різних видах: по-перше, як твердження про існування інтегруючого множника для відомого виразу $\delta Q$ і по—друге, як твердження про неухильне зростання ентропії при реальних адіабатичних процесах. Видається важким вмістити в одне чітке осяжне поле зору ці обидва положення і схопити логічну тотожність другого закону і принципу зростання ентропії. .

Завдяки ревізії другого закону термодинаміки на перший план у якості фундаментального закону термодинаміки виходить принцип існування ентропії, а принцип зростання ентропії ізольованих систем є принципом локальним, статистичним, який, за словами Т. А. Афанасьєвої-Еренфест, виконується "тільки в деякі епохи" .

Гіпотеза теплової смерті Всесвіту

Некритичне узагальнення закономірностей земного досвіду, в якому не враховуються гравітаційні взаємодії, зокрема , поширення висновків другого закону термодинаміки про зростання ентропії ізольованих систем на системи галактичного розміру і на Всесвіт в цілому, де значну роль у формуванні нових зоряних систем відіграють гравітаційні сили, призводило в минулому до антинаукового висновку про теплову смерть Всесвіту. Згідно з сучасними даними, Метагалактика являє собою розширювану систему, яка є нестаціонарною, і тому питання про теплову смерть Всесвіту не можна навіть ставити . Однак сам термін "теплова смерть Всесвіту" іноді використовується для позначення сценарію майбутнього розвитку Всесвіту, згідно з яким Всесвіт так і буде розширюватися до нескінченності в темряву простору, поки не звернеться в розсіяний холодний прах.

Другий закон термодинаміки та критика еволюціонізму

Другий закон термодинаміки (у формулюванні неубування ентропії) іноді використовується критиками еволюційної теорії з метою показати, що розвиток природи у бік ускладнення неможливий. Однак подібне застосування фізичного закону є некоректним, тому що ентропія не убуває тільки в замкнутих системах (порівн. з дисипативною системою), тоді як живі організми та планета Земля в цілому є відкритими системами , . У процесі життєдіяльності живі організми перетворюють енергію одного виду (електромагнітну сонячну, хімічну) в енергію іншого виду — хаотичного руху, тим самим прискорюючи сумарне збільшення ентропії Всесвіту. Незважаючи на"локальне" зменшення ентропії шляхом "впорядкованих" процесів, відбувається сумарне збільшення ентропії Всесвіту, а живі організми є в деякому роді каталізаторами цього процесу. Таким чином, спостерігається виконання другого закону термодинаміки і немає ніякого парадоксу виникнення та існування живих організмів всупереч глобальній тенденції Всесвіту до збільшення "безладу".

Про науково–методичні конференції з термодинаміки в СРСР

В кінці 30-х і в наступні роки зросла роль методичної роботи над курсом термодинаміки. При цьому зріс інтерес до постановки і обґрунтуванню багатьох положень термодинаміки, зокрема другого закону термодинаміки, що призвело до організації та проведенню ряду методичних конференцій з широким залученням професорів, викладачів і фахівців в області термодинаміки. Перші такі конференції були організовані в кінці тридцятих років. Особливо розширеною за складом і кількістю доповідей була конференція, проведена в 1939 році під головуванням академіка М. В. Кирпичова. Наступні конференції, намічені на 1940 і 1941 роки не відбулися, і поновилися після закінчення війни в кінці сорокових і на початку 50х років. У 1962 р. відбулися дві науково-методичні конференції з термодинаміки, одна в Москві, друга в Одесі. Найбільший інтерес представляла московська конференція, під головуванням М. І. Білоконя, в якій були заслухані доповіді з трьох проблем:

1. Основні принципи та особливості розрахункових положень термодинаміки.

2. Взаємини термодинаміки та статистичної фізики.

3. Теоретичні та експериментальні дослідження речовини.

Першій проблемі були присвячені доповіді: М. І. Білоконя: "Постулати, схеми побудови та математичні вирази основних принципів термодинаміки," А.А. Гухмана: Про різні системи обґрунтування другого закону термодинаміки, І. П. Базарова: Термодинаміка систем при від'ємних абсолютних температурах та ін. Особливо жвавими та численними були виступи з першої проблеми, зокрема, з доповіді М. І. Білоконя. На жаль, за словами А. С. Ястржембського, конференція не змогла за цими доповідями дійти будь-яких висновків та рекомендацій. .

У поп-культурі

• Володар таємниць — назва 7-го тому 2-ї книги та 0-ва послідовність однойменного шляху у всесвіті твору.

Джерела

• Афанасьева-Эренфест Т. А. Необратимость, односторонность и второе начало термодинамики // Журнал прикладной физики. — 1928. — Т. 5, № 3—4. — С. 3—30.
• Базаров И. П. Термодинамика. — 5-е вид. — СПб.—М.—Краснодар : Лань, 2010. — 384 с. — (підручники для зво.) — ISBN 978-5-8114-1003-3.
• Белоконь Н. И. Термодинамика. — М. : Госэнергоиздат, 1954. — 416 с.
• Белоконь Н. И. Основные принципы термодинамики. — М. : Недра, 1968. — 112 с.
• Больцман Л.  / від. ред. Л. С. Полак lang =ru. — М. : Наука, 1984. — 590 с. — (Классики науки)
• Большая Советская Энциклопедия / гол. ред. А. М. Прохоров. — 3-е вид. — М. : Советская энциклопедия, 1971. — Т. 5: Вешин — Газли. — 640 с.
• Большая Российская Энциклопедия / гол. ред. Ю. С. Осипов. — М. : Большая Российская Энциклопедия, 2006. — Т. 6: Восьмеричный путь — Германцы. — 768 с. — ISBN 5-85270-335-4.
• Бродянский В. М. Вечный двигатель — прежде и теперь. От утопии — к науке, от науки — к утопии. — М. : Энергоатомиздат, 1989. — 256 с. — (Научно-популярная библиотека школьника) — ISBN 5-283-00058-3..
• Вукалович М. П. Техническая термодинамика. — М. : Энергия, 1968. — 496 с.
• Второе начало термодинамики (сборник) / під. ред. і з перед. А. К. Тимирязева. — М.—Л. : Гостехиздат, 1934. — 311 с.
• Гельфер Я. М. История и методология термодинамики и статистистической физики. — 2-е вид. — М. : Высшая школа, 1981. — 536 с.
• Гухман А. А. Об основаниях термодинамики. — 2-е вид. — М. : ЛКИ, 2010. — 384 с. — ISBN 978-5-382-01105-9.
• Кириллин В. А. и др. Техническая термодинамика. — 4-е вид. — М. : Энергоатомиздат, 1983. — 416 с.
• Марков А. Рождение сложности. Эволюционная биология сегодня: неожиданные открытия и новые вопросы. — М. : Астрель, 2010. — 527 с. — ISBN 978-5-271-24663-0.
• Развитие современной физики / від. ред. Кузнецов Б. Г. — Наука, 1964. — 331 с.

• Різак В., Різак І., Рудавський Е. Кріогенна фізика і техніка. — К. : Наукова думка, 2006. — 512 с. — ISBN 966-00-480-X.

• Рындин В. В. Второе начало термодинамики и его развитие. — м. Павлодар : ПГУ, 2002. — 459 с. — ISBN ISBN 9965-568-70-2.
• Сивухин Д. В. Общий курс физики. — 5-е вид. — М. : Физматлит, 2005. — Т. 2. — 544 с. — ISBN 5-9221-0601-5.
• Тезисы докладов на первой научно- методической конференции по термодинамике / провідний редактор Ершов П. Р. — М. : Гостоптехиздат, 1962.
• Физика. Большой энциклопедический словарь / гол. ред. А. М. Прохоров. — М. : Большая Российская энциклопедия, 1998. — 944 с. — ISBN 5-85270-306-0.
• Хайтун С. Д. Кризис науки как зеркальное отражение кризиса теории познания: кризис теории познания. — М. : Ленанд, 2014. — 448 с. — ISBN 978-5-9710=1296-2.
• Химическая энциклопедия / гол. ред. И. Л. Кнунянц. — М. : Советская энциклопедия, 1988. — Т. 1: Абл — Дар.
• Шамбадаль П.,. Развитие и приложение понятия энтропии. — М. : Наука, 1967. — 280 с.
• Ястржембский А. С. Термодинамика и история её развития. — М.-Л. : Энергия, 1966. — 668 с.
• John Rennie,. 15 Answers to Creationist Nonsense. — USA, 2002. — 1 липня.

Категория: Закони термодинаміки