Ендрю М. Глісон
| Ендрю Метті Глісон | |
|---|---|
| Andrew Mattei Gleason | |
 | |
| Ім'я при народженні | англ. Andrew Mattei Gleason[1] |
| Народився | 4 листопада 1921 Фресно (Каліфорнія) |
| Помер | 17 жовтня 2008 (86 років) Кембридж (Массачусетс) |
| Країна | |
| Діяльність | математик, викладач університету, криптограф |
| Alma mater | Єльський університет (1942)[1] Theodore Roosevelt High Schoold (1938)[1] |
| Галузь | Математика, криптографія |
| Заклад | Гарвардський університет |
| Посада | президент[2][3] |
| Науковий керівник | Джордж Макі[4] |
| Аспіранти, докторанти | |
| Членство | Національна академія наук США Американська академія мистецтв і наук |
| Війна | Друга світова війна[1] і Корейська війна[1] |
| Батько | Генрі Алан Глізон |
| Брати, сестри | Henry Allan Gleasond |
| У шлюбі з | Jean Berko Gleasond[1] |
| Родичі | Andrew Matteid |
| Нагороди |
|
Ендрю Метті Глісон (англ. Andrew Mattei Gleason; 4 листопада 1921 — 17 жовтня 2008) — американський математик, який зробив фундаментальний внесок у різні галузі математики, зокрема у розв'язання п'ятої проблеми Гільберта, був лідером реформ та інновацій у викладанні математики на всіх рівнях.[5][6] Його ім'ям названо теорему Глісона у квантовій логіці та граф Грінвуда-Глісона, важливий приклад у теорії Ремзі.
Будучи молодим морським офіцером часів Другої світової війни, Глісон зламував німецькі та японські військові коди. Після війни він провів всю свою наукову кар'єру в Гарвардському університеті, звідки вийшов на пенсію в 1992 році. Серед його численних академічних і наукових керівних посад були головування на Гарвардському математичному факультеті та в Гарвардському товаристві стипендіатів, а також президентство в Американському математичному товаристві. Майже до кінця свого життя він продовжував консультувати уряд США з питань криптографічної безпеки, а штат Массачусетс — з питань математичної освіти для дітей.
Глісон отримав премію Ньюкомба Клівленда у 1952 році та премію Гун-Ху за видатні заслуги Американського математичного товариства у 1996 році. Був членом Національної академії наук, Американської академії мистецтв і наук та Американського філософського товариства, а також очолював кафедру математики та натурфілософії Голліса в Гарварді.
Ендрю любив повторювати, що математичні доведення «насправді існують не для того, щоб переконати вас у тому, що щось істинне — вони існують для того, щоб показати вам, чому це істинно».[7] У «Повідомленнях Американського математичного товариства» його називали «одним із тихих гігантів математики двадцятого століття, неперевершеним професором, який однаковою мірою присвятив себе науці, викладанню та служінню».[8]

Глісон народився у Фресно, штат Каліфорнія, наймолодшим з трьох дітей; його батько Генрі Глісон був ботаніком і членом товариства «Мейфлауер», а мати — дочкою швейцарсько-американського винороба Ендрю Маттеї.[7] Його старший брат Генрі-молодший став лінгвістом.[9] Він виріс у Бронксвіллі, штат Нью-Йорк, де його батько був куратором Нью-Йоркського ботанічного саду.[7]
Після нетривалого навчання в середній школі Берклі (Берклі, Каліфорнія) він закінчив середню школу Рузвельта в Йонкерсі, вигравши стипендію Єльського університету[7]. Хоча математична освіта Глісона обмежувалася лише деякими самоучками, єльський математик Вільям Реймонд Лонглі запропонував йому спробувати курс механіки, який зазвичай призначався для студентів молодших курсів. Через місяць він також записався на курс диференціальних рівнянь («здебільшого заповнений студентами старших курсів»). Коли Ейнар Гілле тимчасово замінив постійного викладача, Глісон знайшов стиль Гілле «неймовірно новітнім … У нього був погляд на математику, який дуже відрізнявся… Це був дуже важливий досвід для мене. Після цього я прослухав багато курсів Гілле», в тому числі, на другому курсі, реальний аналіз на рівні аспірантури. «Починаючи з того курсу з Гілле, я почав мати певне уявлення про те, що таке математика».[7]
Під час навчання в Єльському університеті він тричі (1940, 1941 і 1942) брав участь у нещодавно заснованому математичному конкурсі Вільяма Лоуелла Путнема, завжди потрапляючи до п'ятірки найкращих конкурсантів у країні (що робить його другим триразовим стипендіатом Путнема).[10]
Після того, як японці напали на Перл-Гарбор під час його останнього року навчання, Глісон подав заяву на вступ до ВМС США,[11] а по закінченні університету приєднався до команди, яка працювала над зломом японських військово-морських кодів.[7] (Серед інших членів цієї команди були його майбутній співробітник Роберт Грінвуд і професор Єльського університету Маршалл Холл-молодший).[11] Він також співпрацював з британськими дослідниками, які атакували німецький шифр «Енігма»; Алан Тюрінг, який провів багато часу з Глісоном під час візиту до Вашингтона, у звіті про свій візит назвав його «геніальним молодим математиком-випускником Єльського університету».[11]

У 1946 році за рекомендацією колеги по флоту Дональда Говарда Мензеля Глісон був призначений молодшим науковим співробітником Гарварду. Першою метою програми Junior Fellows було дозволити молодим науковцям, які демонстрували надзвичайний потенціал, оминути тривалий процес здобуття ступеня доктора філософії; через чотири роки Гарвард призначив Глісона асистентом професора математики,[7] хоча його майже одразу відкликали до Вашингтона за криптографічну роботу, пов'язану з Корейською війною.[7] Він повернувся до Гарварду восени 1952 року і невдовзі опублікував найважливіші з своїх результатів щодо п'ятої проблеми Гільберта. Наступного року Гарвард надав йому посаду професора.[7][12]
У січні 1959 року він одружився з Джин Берко,[7] з якою познайомився на вечірці, там звучала музика Тома Лерера.[7] Берко, психолінгвіст, багато років працювала в Бостонському університеті.[12] У них було три доньки.
У 1969 році Глісон очолив кафедру математики та натурфілософії імені Голіса. Заснована у 1727 році, ця кафедра є найстарішою професорською кафедрою у США[5][13], що має наукові стипендії. Він вийшов на пенсію з Гарварду в 1992 році, але продовжував активно служити Гарварду (наприклад, як голова Товариства стипендіатів)[14] і математиці: зокрема, просуваючи Гарвардський проект реформування обчислень[15] і працюючи з Массачусетською радою з питань освіти.
Голісон помер у 2008 році у зв'язку із ускладненнями після операції.[5][6]

Глісон сказав, що йому «завжди подобалося допомагати іншим людям з математикою», а його колега сказав, що він «вважав викладання математики — як і саму математику — не лише важливою, але й по-справжньому цікавою справою». У чотирнадцять років, під час свого короткого навчання в середній школі Берклі, він не лише не нудьгував на геометрії в першому семестрі, але й допомагав іншим учням з домашніми завданнями, в тому числі й тим, хто проходив другу половину курсу, яку він незабаром почав перевіряти.[7][16]
У Гарварді він «регулярно викладав на всіх рівнях»,[15] включно з адміністративно обтяжливими багатосекційними курсами. На одному з курсів Глісону подарували гравюру Пікассо «Мати з дитиною» в рамці на знак визнання його турботи про них.[17]
У 1964 році він створив «перший з „проміжних“ курсів, які зараз повсюдно використовуються на математичних спеціальностях, лише за двадцять років до свого часу».[15] Такий курс призначений навчити нових студентів, які звикли до зазубрювання математики в середній школі, як міркувати абстрактно і будувати математичні доведення, про яку писав один з рецензентів так:
Це дуже незвичайна книжка… Кожен працюючий математик, звичайно, знає різницю між млявим ланцюжком формалізованих пропозицій і «відчуттям», яке має (або намагається отримати) математична теорія, і, ймовірно, погодиться, що допомогти студенту досягти цього «внутрішнього» погляду є кінцевою метою математичної освіти; але він, як правило, відмовляється від будь-яких спроб успішно досягти цього, окрім як через усне викладання. Оригінальність автора полягає в тому, що він спробував досягти цієї мети в підручнику, і, на думку рецензента, він досягнув значного успіху в цьому майже неможливому завданні. Більшість читачів, ймовірно, будуть у захваті (як і рецензент), знайшовши сторінку за сторінкою копіткі обговорення і пояснення стандартних математичних і логічних процедур, завжди написані в найсприятливішому стилі, який не шкодує зусиль для досягнення максимальної ясності, не впадаючи при цьому у вульгарність, яка так часто затьмарює подібні спроби.[18]

Але «талант викладу» Глісона не завжди означав, що читач буде просвітлений без його власних зусиль. Навіть у службовій записці воєнного часу, присвяченій терміновому розшифруванню німецького шифру «Енігма», Глісон та його колеги писали про це:
Читач може здивуватися, чому так багато залишено на розсуд читача. Книгу про плавальні рухи може бути приємно читати, але людина повинна практикувати ці рухи, перебуваючи у воді, перш ніж вона зможе претендувати на звання плавця. Отже, якщо читач бажає дійсно володіти знаннями для відновлення проводки з глибини, нехай читач візьме папір і олівці, використовуючи, можливо, чотири кольори, щоб уникнути плутанини у з'єднувальних ланках, і візьметься за роботу.
Нотатки й вправи з ймовірності та статистики, які він писав для лекцій для зламників кодів під час війни (див. нижче), десятиліттями використовувалися під час підготовки Агентства національної безпеки; вони були публічно опубліковані в 1985 році.[16]
У статті 1964 року в Science статті, Глісон писав про очевидний парадокс спроби пояснити математику нематематикам:
Відомо, що неспеціалістам важко передати належне враження про межі математики. Зрештою, складність полягає в тому, що математика є простішим предметом, ніж інші науки. Як наслідок, багато важливих первинних проблем предмета, тобто проблем, які можуть бути зрозумілі розумному сторонньому спостерігачеві, були або вирішені, або доведені до точки, де явно потрібен непрямий підхід. Значна частина чисто математичних досліджень стосується проблем вторинного, третинного або вищого порядку, саму постановку яких навряд чи можна зрозуміти, доки не опануєш великий обсяг технічної математики.[19].

Глісон був першим головою консультативного комітету Шкільної дослідницької групи з математики[en], яка допомогла визначити «Нову математику[en]» 1960-х років — амбітні зміни у викладанні математики в американській початковій та старшій школі, що наголошували на розумінні концепцій, а не на зазубрюванні алгоритмів. Глісон «завжди цікавився тим, як люди вчаться»; в рамках «Нової математики» він проводив більшість ранків протягом кількох місяців з другокласниками. Кілька років по тому він виступив з промовою, в якій описав свою мету:
Щоб з'ясувати, як багато вони можуть з'ясувати для себе, за умови відповідних занять і правильного керівництва. Наприкінці його виступу хтось запитав Енді, чи хвилювало його коли-небудь, що викладання математики маленьким дітям - це не те, чим повинні займатися викладачі науково-дослідних установ. "Його швидка і рішуча відповідь: "Ні, я взагалі про це не думав. Я розважався!"
У 1986 році він допоміг заснувати Консорціум з математики, який опублікував успішну і впливову серію підручників з «реформи математики» для коледжів і середніх шкіл, з попереднього обчислення, математичного аналізу та інших дисциплін. Його «кредо для цієї програми, як і для всього його викладання, полягало в тому, що ідеї повинні в рівній мірі базуватися на геометрії для візуалізації концепцій, обчисленнях для заземлення в реальному світі та алгебраїчних маніпуляціях для сили».[12] Однак програма зазнала жорсткої критики з боку математичної спільноти за відсутність таких тем, як теорема про середнє арифметичне,[21] а також за брак математичної строгості.[22][23][24]

Під час Другої світової війни Глісон входив до складу OP-20-G, групи радіорозвідки та криптоаналізу ВМС США. Одним із завдань цієї групи, у співпраці з британськими криптографами з Блетчлі-Парку, такими як Алан Тюрінг, було проникнення в німецькі мережі машинного зв'язку «Енігма». Британці досягли великого успіху з двома з цих мереж, але третя, яка використовувалася для німецько-японської військово-морської координації, залишилася непорушною через помилкове припущення, що вона використовувала спрощену версію «Енігми». Після того, як Маршалл Хол з OP-20-G помітив, що певні метадані в передачах Берлін-Токіо використовували набори літер, відмінні від тих, що використовувалися в метаданих Токіо-Берлін, Глісон висунув гіпотезу, що відповідними незашифрованими наборами літер були A-M (в одному напрямку) і N-Z (в іншому), а потім розробив нові статистичні тести, за допомогою яких він підтвердив цю гіпотезу. Результатом стало рутинне розшифрування цієї третьої мережі до 1944 року. (Ця робота також включала більш глибоку математику, пов'язану з групами перестановок і проблемою ізоморфізму графів).[11]
Потім OP-20-G звернулася до шифру японського флоту «Корал». Ключовим інструментом для атаки на «Корал» була «милиця Глісона», форма границі Чернова на хвостових розподілах сум незалежних випадкових величин. Засекречена робота Глісона над цією границею випередила роботу Чернова на десять років.[11]
Наприкінці війни він зосередився на документуванні роботи OP-20-G та розробці систем для навчання нових криптографів.[11]
У 1950 році Глісон повернувся на дійсну військову службу під час Корейської війни, де служив лейтенант-командером у комплексі «Небраска Авеню» (який набагато пізніше став домом для Відділу кібербезпеки Міністерства національної безпеки США). Його криптографічна робота цього періоду залишається засекреченою, але відомо, що він наймав на роботу математиків і навчав їх криптоаналізу. Він входив до складу консультативних рад Агентства національної безпеки та Інституту оборонного аналізу, і продовжував набирати співробітників і консультувати військових з питань криптоаналізу майже до кінця свого життя.[11]
Глісон зробив фундаментальний внесок у різні галузі математики, включаючи теорію груп Лі,[25] квантову механіку та комбінаторику.[26] Згідно з відомою класифікацією Фрімена Дайсона, який поділив математиків на птахів і жаб,[27] Глісон був жабою: він працював радше як розв'язувач проблем, ніж як візіонер, що формулює грандіозні теорії.[8]

У 1900 році Давид Гільберт запропонував 23 проблеми, які, на його думку, будуть центральними для математичних досліджень наступного століття. П'ята проблема Гільберта стосувалося характеристики груп Лі за їх дією на топологічні простори: якою мірою їх топологія надає інформацію, достатню для визначення їх геометрії?
«Обмежена» версія п'ятої проблеми Гільберта (розв'язана Глісоном) запитує, зокрема, чи кожна локально евклідова топологічна група є групою Лі. Тобто, якщо група G має структуру топологічного многовиду, чи можна цю структуру посилити до реальної аналітичної структури, так, щоб в межах будь-якого околу елемента G груповий закон визначався збіжним степеневим рядом, і щоб околиці, що перетинаються, мали сумісні визначення степеневих рядів? До роботи Глісона окремі випадки цієї проблеми розв'язували, зокрема, Лейтзен Егберт Ян Брауер, Джон фон Нейман, Лев Понтрягін та Гаррет Біркгоф.[25][28]

Інтерес Глісона до п'ятої проблеми розпочався наприкінці 1940-х років під впливом курсу, який він прослухав у Джорджа Макі.[7] У 1949 році він опублікував статтю, в якій описав властивість груп Лі «без малих підгруп» (існування околу тотожності, в якому не існує жодної нетривіальної підгрупи), що зрештою стала вирішальною для її розв'язання.[25] Його стаття 1952 року на цю тему, разом із статтею, опублікованою одночасно Діном Монтгомері та Лео Зіппіном, ствердно розв'язує обмежену версію п'ятої проблеми Гільберта, показуючи, що справді кожна локально евклідова група є групою Лі.[25][28] Внесок Глісона полягав у доведенні того, що це вірно, коли G має властивість відсутності малих підгруп; Монтгомері та Зіпін показали, що кожна локально евклідова група має цю властивість.[25][28] Як розповідав Глісон, ключовим моментом його доведення було застосування того факту, що монотонні функції є диференційовними майже скрізь[9]. Знайшовши розв'язок, він взяв тижневу відпустку, щоб написати його, і він був надрукований в «Анналах математики» разом зі статтею Монтгомері та Зіппіна; інша стаття, написана роком пізніше Хідехіко Ямабе, вилучила деякі технічні побічні умови з доведення Глісона.[7]
«Необмежена» версія п'ятої проблеми Гільберта, ближча до оригінального формулювання Гільберта, розглядає як локально евклідову групу G, так і інший многовид M, на якому G має неперервну дію. Гільберт запитав, чи можна в цьому випадку надати M і дії G реальну аналітичну структуру. Було швидко зрозуміло, що відповідь негативна, після чого увага зосередилась на обмеженій задачі.[25][28] Однак, з деякими додатковими припущеннями про гладкість G і M, все ж таки можна довести існування реальної аналітичної структури на груповій дії.[25][28] Гіпотеза Гільберта-Смітта, яку досі не розв'язано, містить решту труднощів цього випадку.[29]

Правило Борна стверджує, що спостережувані властивості квантової системи визначаються ермітовим оператором у сепарабельному гільбертовому просторі, що єдиним спостережуваним значенням властивості є власне значення оператора, а ймовірність системи є специфічною характеристикою значення в значенні дорівнює квадрату абсолютного значення комплексного числа, отриманого проектуванням вектора стану (точка в гільбертовому просторі) на відповідний власний вектор. Джордж Макі запитав, чи є закон Борна необхідним наслідком певного набору аксіом квантової механіки, а точніше, чи кожна міра на просторовій проекційній решітці Гільберта може бути визначена додатним оператором із одиничним слідом. Хоча Річард Кедісон показав, що це не справедливо для двовимірних гільбертових просторів, теорема Глісона (опублікована в 1957 році) показала, що це справедливо для вищих вимірів.[29]
Теорема Глісона передбачає неіснування певних типів теорій прихованих параметрів для квантової механіки, посилюючи попередній аргумент Джона фон Неймана. Фон Нейман стверджував, що теорії прихованих змінних неможливі, але (як зазначає Грета Герман) його демонстрація робила припущення, що квантові системи підкоряються формі адитивності очікування для некомутативних операторів, яка може бути невірною апріорі. У 1966 році Джон Стюарт Белл показав, що теорема Глісона може бути використана для усунення цього зайвого припущення з аргументу фон Неймана.[30]
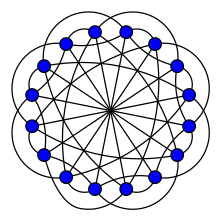
Число Ремзі R (k, l) — це найменше число r таке, що кожен граф із щонайменше r вершинами містить k клік вершин або l незалежних наборів вершин. Обчислення чисел Рамсі вимагає значних зусиль; коли max(k, l) ≥ 3, лише кінцева їх кількість відома, і точне обчислення R (6,6) вважається недосяжним.[31] У 1953 році розрахунок R(3,3) був поставлений як проблема на змаганнях Патнема; у 1955 році, мотивований цією проблемою,[32] Глісон і його співавтор Роберт Е. Грінвуд працювали над обчисленням чисел Ремзі, і довели, що R(3,4)=9, R(3,5)=14 і R(4,4)=18. З тих пір було знайдено лише п'ять таких значень.[33] У тій самій статті 1955 року Грінвуд і Глісон також обчислили поліхроматичне число Ремзі R (3,3,3): найменше число r, якщо повний граф із r вершинами має ребра, пофарбовані в три кольори, тоді він повинен містити монохроматичний трикутник. Як показали, R (3,3,3) = 17; це залишається єдиним нетривіальним багатоколірним числом Ремзі, точне значення якого відоме.[33]
Як частину свого доказу вони використали алгебраїчні конструкції, щоб показати, що повний граф із 16 вершинами можна розкласти на три різні версії 5-правильного графа без трикутників із 16 вершинами та 40 ребрами[26][34].(іноді його називають графом Грінвуда-Глісона[35])
Рональд Грем пише, що робота Грінвуда і Глісона «сьогодні визнана класикою в розвитку теорії Ремзі».[32] Наприкінці 1960-х років Глісон став науковим керівником Джоела Спенсера, який прославився завдяки своєму внеску в теорію Ремзі.[26][35]

Глісон опублікував небагато робіт з теорії кодування, але вони були впливовими[26] і включали «багато фундаментальних ідей та ранніх результатів» в алгебраїчній теорії кодування.[36] Протягом 1950-х і 1960-х років він відвідував щомісячні зустрічі з теорії кодування з Вірою Плесс та іншими в Кембриджській дослідницькій лабораторії ВПС.[37] Плес, яка раніше працювала в галузі абстрактної алгебри, але за цей час стала одним з провідних світових експертів з теорії кодування, пише, що «ці щомісячні зустрічі були тим, заради чого я жила». Вона часто ставила перед Глісоном свої математичні проблеми і була винагороджена швидкою і глибокою відповіддю.[26]
Теорема Глісона-Пранжа названа на честь роботи Глісона з дослідником AFCRL Юджином Пранжем[en]; спочатку була опублікована в дослідницькому звіті AFCRL 1964 року Х. Ф. Маттсоном-молодшим і Е. Ф. Ассмусом-молодшим. Вона стосується квадратичного залишкового коду порядку n, розширеного за рахунок додавання одного біта перевірки на парність. Ця «чудова теорема»[38] показує, що цей код є високосиметричним, маючи проєктивну лінійну групу PSL2(n), як підгрупу своїх симетрій.[26][38]
Глісон є тезкою поліномів Глісона, системи поліномів, які генерують вагові перелічувачі лінійних кодів.[26][39] Ці поліноми набувають особливо простої форми для самодуальних кодів: у цьому випадку їх всього два, два двовимірні поліноми x2 + y2 і x8 + 14x2y2 + y8.[26] Учениця Глісона Джессі Мак-Вільямс продовжила роботу Глісона в цій галузі, довівши зв'язок між ваговими перелічувачами кодів та їхніми двоїстими, відомий як тотожність Мак-Вільямса.[26]
У цій галузі Глісон також зробив новаторську роботу в експериментальній математиці, провівши комп'ютерні експерименти в 1960 році. У цій роботі він вивчав середню відстань до кодового слова для коду, пов'язаного з грою перемикання Берлекампа.[12][40]
Глісон заснував теорію алгебр Діріхле[en][41] та зробив інші математичні внески, включаючи роботи з скінченної геометрії[42] та нумераційної комбінаторики перестановок.[8] (У 1959 році він писав, що його дослідницькі «побічні» інтереси включали «інтенсивний інтерес до комбінаторних проблем»).[5] Крім того, він був не проти публікувати дослідження з більш елементарної математики, такі як виведення множини багатокутників, які можна побудувати за допомогою циркуля, лінійки та трисектора кута.[8]

У 1952 році за роботу над п'ятою проблемою Гільберта Глісон був нагороджений Премією Ньюкомба Клівленда[43] Американської асоціації сприяння розвитку науки.[5] Обраний до Національної академії наук та Американського філософського товариства, був членом Американської академії мистецтв і наук,[7][12] а також входив до складу Математичного товариства Франції.[5]
У 1981 і 1982 роках він президент Американського математичного товариства[7], а також у різний час обіймав численні інші посади в професійних і наукових організаціях, зокрема очолював Гарвардський факультет математики.[44] У 1986 році він був головою організаційного комітету Міжнародного конгресу математиків у Берклі, Каліфорнія.
У 1996 році Гарвардське товариство стипендіатів провело спеціальний симпозіум на честь Глісона у зв'язку з його виходом на пенсію після семи років на посаді голови;[14] того ж року Математична асоціація Америки нагородила його премією Юе-Гін Гун і доктора Чарльза Ю. Ху за видатні заслуги в математиці.[45] Колишній президент Асоціації писав:
Роздумуючи про кар'єру Енді Глісона і захоплюючись нею, ви, природно, звертаєтесь до всієї професії математика: розробка і викладання курсів, консультування з питань освіти на всіх рівнях, проведення досліджень, консультування користувачів математики, виконання ролі лідера професії, культивування таланту і служіння своїй установі. Енді Глісон - це та рідкісна людина, яка робить все це чудово.[18]
Після його смерті 32-сторінкова збірка статей була опублікована в Повідомленнях Американського математичного товариства, щоб вшанувати «життя та роботу цього видатного американського математика»[46] і назвати його «мовчазним гігантом математики двадцятого століття», досконалий математик". Професори однаково віддані науці, навчанню та служінню".[8]
- Наукові праці
- Gleason, A. M. (1952), Однопараметричні підгрупи та п'ята проблема Гільберта, Proceedings of the International Congress of Mathematicians, Cambridge, Mass., 1950, Vol. 2 (PDF), Providence, R. I.: American Mathematical Society, с. 451—452, MR 0043788, архів оригіналу (PDF) за 14 грудня 2014, процитовано 5 квітня 2013
- —— (1956), Скінченні площини Фано, American Journal of Mathematics, 78 (4): 797—807, doi:10.2307/2372469, JSTOR 2372469, MR 0082684.
- —— (1957), Measures on the closed subspaces of a Hilbert space, Journal of Mathematics and Mechanics, 6 (4): 885—893, doi:10.1512/iumj.1957.6.56050, MR 0096113.
- —— (1958), Проекційні топологічні простори, Іллінойський математичний журнал, 2 (4A): 482—489, doi:10.1215/ijm/1255454110, MR 0121775, Zbl 0083.17401.
- —— (1967), Характеристика максимальних ідеалів, Journal d'Analyse Mathématique, 19: 171—172, doi:10.1007/bf02788714, MR 0213878, S2CID 121062823.
- —— (1971), Вагові поліноми самоподвійних кодів та тотожності Мак-Вільямса, Actes du Congrès International des Mathématiciens (Nice, 1970), Tome 3, Paris: Gauthier-Villars, с. 211—215, MR 0424391.
- Greenwood, R. E.; Gleason, A. M. (1955), Комбінаторні відношення та хроматичні графи, Canadian Journal of Mathematics, 7: 1—7, doi:10.4153/CJM-1955-001-4, MR 0067467, S2CID 124255697.
- Книги
- Gleason, Andrew M. (1966), Fundamentals of Abstract Analysis, Addison-Wesley Publishing Co., Reading, Mass.-London-Don Mills, Ont., MR 0202509. Виправлене перевидання, Бостон: Jones and Bartlett, 1991, MR1140189.
- ——; Greenwood, Robert E.; Kelly, Leroy Milton (1980), The William Lowell Putnam Mathematical Competition: Problems and Solutions 1938–1964, Mathematical Association of America, ISBN 978-0-88385-462-4, MR 0588757.
- ——; Penney, Walter F.; Wyllys, Ronald E. (1985), Elementary Course in Probability for the Cryptanalyst, Laguna Hills, CA: Aegean Park Press. Некласифіковане перевидання книги, вперше опублікованої в 1957 році Агентством національної безпеки, Управлінням досліджень і розробок, Відділом математичних досліджень.
- ——; Hughes-Hallett, Deborah (1994), Calculus, Wiley. З моменту своєї першої публікації ця книга витримала багато різних видань і варіацій з додатковими співавторами.
- Плівка
- Gleason, Andrew M. (1966), Нім та інші ігри з орієнтованою графікою, Mathematical Association of America. 63 minutes, black & white. Produced by Richard G. Long and directed by Allan Hinderstein.
- Критика Беллом доказу фон Неймана
- Просте число Пірпонта, клас простих чисел, який Глісон вважав нескінченним
- ↑ а б в г д е Архів історії математики Мактьютор — 1994.
- ↑ https://mathshistory.st-andrews.ac.uk/Honours/AMSPresidents/
- ↑ http://www.ams.org/about-us/presidents/46-gleason
- ↑ https://iiif.lib.harvard.edu/manifests/view/drs:427334755$46i
- ↑ а б в г д е Джон Дж. О'Коннор та Едмунд Ф. Робертсон. Andrew Mattei Gleason в архіві MacTutor (англ.)
- ↑ а б Castello, Caitlin (20 жовтня 2008), Andrew Gleason; helped solve vexing geometry problem, Boston Globe, архів оригіналу за 20 травня 2013.
- ↑ а б в г д е ж и к л м н п р с т Albers, Donald J.; Alexanderson, Gerald L.; Reid, Constance, ред. (1990), Andrew M. Gleason, More Mathematical People, Harcourt Brace Jovanovich, с. 86.
- ↑ а б в г д Bolker, Ethan D. (November 2009), Bolker, Ethan D. (ред.), 50+ years ... (PDF), Andrew M. Gleason 1921–2008, Notices of the American Mathematical Society, 56 (10): 1237—1239.
- ↑ а б Henry A. Gleason Papers, Mertz Library, New York Botanical Garden, архів оригіналу за 12 липня 2010, процитовано 9 квітня 2013
- ↑ Gallian, Joseph A., The Putnam Competition from 1938–2013 (PDF), процитовано 10 квітня 2016.
- ↑ а б в г д е ж Burroughs, John; Lieberman, David; Reeds, Jim (November 2009), Bolker, Ethan D. (ред.), The secret life of Andrew Gleason (PDF), Andrew M. Gleason 1921–2008, Notices of the American Mathematical Society, 56 (10): 1239—1243.
- ↑ а б в г д Mazur, Barry; Gross, Benedict; Mumford, David (December 2010), Andrew Gleason, 4 November 1921 – 17 October 2008 (PDF), Proceedings of the American Philosophical Society, 154 (4): 471—476, архів оригіналу (PDF) за 20 December 2016, процитовано 10 квітня 2016.
- ↑ Walsh, Colleen (3 травня 2012), The oldest endowed professorship: 1721 gift led to long line of Hollis Chair occupants at Divinity School, Harvard Gazette.
- ↑ а б Ruder, Debra Bradley (9 травня 1996), Symposium Will Celebrate Gleason and Society of Fellows, Harvard Gazette.
- ↑ а б в Hughes-Hallett, Deborah; Stevens, T. Christine; Tecosky-Feldman, Jeff; Tucker, Thomas (November 2009), Bolker, Ethan D. (ред.), Andy Gleason: teacher (PDF), Andrew M. Gleason 1921–2008, Notices of the American Mathematical Society, 56 (10): 1260—1265.
- ↑ а б Bolker, Ethan D. (1976-03). Simplical Geometry and Transportation Polytopes. Transactions of the American Mathematical Society. Т. 217. с. 121. doi:10.2307/1997562. ISSN 0002-9947. Процитовано 28 жовтня 2023.
- ↑ Bolker, Ethan D; Gleason, Andrew M (1980-09). Counting permutations. Journal of Combinatorial Theory, Series A. Т. 29, № 2. с. 236—242. doi:10.1016/0097-3165(80)90012-6. ISSN 0097-3165. Процитовано 28 жовтня 2023.
- ↑ а б Pollak, H. O. (February 1996), Нагорода Юе-Гін Ґунґа і доктора Чарльза Ю. Ху за видатні заслуги Ендрю Глісона, American Mathematical Monthly, 103 (2): 105—106, doi:10.1080/00029890.1996.12004708, JSTOR 2975102.
- ↑ Андрю Глісон (Andrew M. Gleason). Andrew M. Gleason. "Еволюція активної математичної теорії", Science 31 (липень 1964), с. 451-457.
- ↑ Hughes-Hallett, Deborah; Stevens, T. Christine; Tecosky-Feldman, Jeff; Tucker, Thomas (November 2009), Bolker, Ethan D. (ред.), Andy Gleason: teacher (PDF), Notices of the American Mathematical Society, 56 (10): 1260—1265.
- ↑ Lock, Patti Frazer (1994), Reflections on the Harvard calculus approach, PRIMUS: Problems, Resources, and Issues in Mathematics Undergraduate Studies, 4 (3): 229—234, doi:10.1080/10511979408965753.
- ↑ Wu, H. (1997), The Mathematics Education Reform: Why You Should be Concerned and What You Can Do (PDF), American Mathematical Monthly, 104 (10): 946—954, doi:10.2307/2974477, JSTOR 2974477.
- ↑ Mac Lane, Saunders (1997), On the Harvard Consortium Calculus (PDF), Letters to the Editor, Notices of the American Mathematical Society, 44 (8): 893.
- ↑ Klein, David; Rosen, Jerry (1997), Calculus Reform—For the $Millions (PDF), Notices of the American Mathematical Society, 44 (10): 1324—1325.
- ↑ а б в г д е ж Palais, Richard (November 2009), Bolker, Ethan D. (ред.), Gleason's contribution to the solution of Hilbert's Fifth Problem (PDF), Andrew M. Gleason 1921–2008, Notices of the American Mathematical Society, 56 (10): 1243—1248.
- ↑ а б в г д е ж и к Spencer, Joel J. (November 2009), Bolker, Ethan D. (ред.), Andrew Gleason's discrete mathematics (PDF), Andrew M. Gleason 1921–2008, Notices of the American Mathematical Society, 56 (10): 1251—1253.
- ↑ Dyson, Freeman (February 2009), Birds and frogs (PDF), Notices of the American Mathematical Society, 56 (2): 212—223.
- ↑ а б в г д Illman, Sören (2001). Hilbert's Fifth Problem: Review | Journal of Mathematical Sciences. Journal of Mathematical Sciences. Т. 105, № 2. с. 1843—1847. doi:10.1023/A:1011323915468. Процитовано 28 жовтня 2023.
- ↑ а б See, e.g., Pardon, John (2013), The Hilbert–Smith conjecture for three-manifolds, Journal of the American Mathematical Society, т. 26, № 3, с. 879—899, arXiv:1112.2324, doi:10.1090/s0894-0347-2013-00766-3, S2CID 96422853.
- ↑ Crawford, Leila (2007-02). Chew on This: Everything You Don't Want to Know about Fast Food:Chew on This: Everything You Don't Want to Know about Fast Food. Gastronomica. Т. 7, № 1. с. 117—117. doi:10.1525/gfc.2007.7.1.117. ISSN 1529-3262. Процитовано 19 листопада 2023.
- ↑ Spencer, Joel J. (1994), Ten Lectures on the Probabilistic Method, SIAM, с. 4, ISBN 978-0-89871-325-1
- ↑ а б Graham, R. L. (1992), Roots of Ramsey theory, у Bolker, E.; Cherno, P.; Costes, C.; Lieberman, D. (ред.), Andrew M. Gleason, Glimpses of a Life in Mathematics (PDF), с. 39—47.
- ↑ а б Radziszowski, Stanisław (22 серпня 2011), Small Ramsey Numbers, Electronic Journal of Combinatorics, DS1, архів оригіналу за 18 жовтня 2012, процитовано 5 квітня 2013.
- ↑ Sun, Hugo S.; Cohen, M. E. (1984), An easy proof of the Greenwood-Gleason evaluation of the Ramsey number R(3,3,3) (PDF), The Fibonacci Quarterly, 22 (3): 235—238, MR 0765316.
- ↑ а б Ендрю М. Глісон(англ.) у проєкті «Математична генеалогія».
- ↑ Review of The Mathematical Theory of Coding, E. F. Assmus, Jr. (1977), SIAM Review, 19 (1): 175—176, doi:10.1137/1019032
- ↑ Pless, Vera (September 1991), In Her Own Words, Notices of the AMS, 38 (7): 702—706, архів оригіналу за 4 березня 2016, процитовано 6 травня 2013.
- ↑ а б Blahut, R. E. (September 2006), The Gleason-Prange theorem, IEEE Trans. Inf. Theory, Piscataway, NJ, USA: IEEE Press, 37 (5): 1269—1273, doi:10.1109/18.133245.
- ↑ Pless, Vera (2011), 8.4 Gleason polynomials, Introduction to the Theory of Error-Correcting Codes, Wiley Series in Discrete Mathematics and Optimization, т. 48 (вид. 3rd), John Wiley & Sons, с. 134—138, ISBN 978-1-118-03099-8.
- ↑ Brown, Thomas A.; Spencer, Joel H. (1971), Minimization of matrices under line shifts, Colloquium Mathematicum, 23: 165—171, 177, doi:10.4064/cm-23-1-165-171, MR 0307944
- ↑ Wermer, John (November 2009), Bolker, Ethan D. (ред.), Gleason's work on Banach algebras (PDF), Andrew M. Gleason 1921–2008, Notices of the American Mathematical Society, 56 (10): 1248—1251.
- ↑ See his 1956 paper «Finite Fano planes».
- ↑ AAAS Newcomb Cleveland Prize, American Association for the Advancement of Science, архів оригіналу за 7 червня 2011, процитовано 10 квітня 2016.
- ↑ Hironaka to Teach Math, Harvard Crimson, 23 жовтня 1967
- ↑ Yueh-Gin Gung and Dr. Charles Y. Hu Award for Distinguished Service, Mathematics Association of America, процитовано 5 серпня 2016.
- ↑ Features (PDF), Notices of the American Mathematical Society, 56 (10), November 2009: 1227.
- Gleason, Andrew M. (1966), Nim and other oriented-graph games, Mathematical Association of America. 63 minutes, black & white. Produced by Richard G. Long and directed by Allan
- Народились 4 листопада
- Народились 1921
- Померли 17 жовтня
- Померли 2008
- Випускники Єльського університету
- Члени і члени-кореспонденти Національної академії наук США
- Члени Американської академії мистецтв і наук
- Топологи
- Персоналії:Фресно
- Викладачі Гарвардського університету
- Графісти
- Математичні аналітики
- Криптографи США
- Президенти Американського математичного товариства
- Уродженці Фресно

