Задача про перебірливу наречену

Графіки ймовірностей отримання найкращого кандидата (червоні кружечки) з n заявок і k/n (сині хрестики), де k — розмір вибірки

Задача про перебірливу наречену, або проблема зупинки вибору — демонстрація застосування теорії оптимальної зупинки, яка широко вивчається в галузі прикладної ймовірності, статистики та теорії прийняття рішень. Вона також відома як проблема секретаря, проблема приданого султана, проблема метушливого залицяльника, гра гугол і проблема найкращого вибору. Її рішення також відоме як правило 37 %.

Основний варіант постановки проблеми такий: уявіть адміністратора, який хоче найняти найкращого секретаря з $n$ претендентів на відповідну посаду; претенденти можуть бути оцінені за рейтингом. Претенденти опитуються по черзі у випадковому порядку. Рішення щодо кожного конкретного претендента приймається відразу після співбесіди. Після відмови претендент не може бути прийнятий на роботу. Під час співбесіди адміністратор отримує достатньо інформації, щоб оцінити рейтинг претендента серед усіх опитаних на даний момент претендентів, але немає можливості порівняти з претендентами, які ще не розглядалися. Питання полягає в оптимальній стратегії (зупинки вибору) щоб максимізувати ймовірність вибору найкращого претендента. Якщо рішення можна відкласти до кінця, задачу можна вирішити за допомогою простого алгоритму вибору максимального відстеження поточного максимуму (і претендента, який його досяг), і вибору загального максимуму в кінці. Складність полягає в тому, що рішення потрібно приймати негайно.

Найкоротший точний доказ, відомий на сьогоднішній день, забезпечується алгоритмом шансів. Він передбачає, що оптимальна ймовірність виграшу завжди принаймні $1/e$ (де e — основа натурального логарифма), і що це справедливо у більш загальному випадку. Правило оптимальної зупинки передбачає стратегію відмови першим $\sim n/e$ які проходять співбесіду, а потім вибору першого претендента, який є кращим за всіх претендентів, опитаних на даний момент (або продовження до останнього претендента, якщо цього ніколи не відбувається). Іноді цю стратегію називають правилом зупинки $1/e$, оскільки ймовірність зупинитися на найкращому претенденті за допомогою цієї стратегії вже приблизно $1/e$ для помірних значень $n$. Одна з причин, чому проблемі секретаря приділено так багато уваги, полягає в тому, що оптимальна стратегія для цієї проблеми (правило зупинки) проста і вибирає єдиного найкращого кандидата приблизно в 37 % випадків, незалежно від того, чи є 100 чи 100 мільйонів претендентів.

Формулювання

Хоча існує багато варіацій, основну проблему можна сформулювати так:

1. Існує єдине вакантне місце.
2. Є n претендентів на посаду і значення n відоме.
3. Про кожного претендента можна сказати, кращий він за іншого чи гірший.
4. Претенденти опитуються послідовно у випадковому порядку, причому кожен порядок є однаково ймовірним.
5. Одразу після співбесіди претендент приймається або відхиляється, і рішення не підлягає скасуванню.
6. Рішення прийняти або відхилити претендента може ґрунтуватися лише на відносних рангах претендентів, з якими на даний момент було проведено співбесіду.
7. Метою загального рішення є найвища ймовірність вибору найкращого претендента з усієї групи. Це еквівалентно максимізації очікуваної нагороди, при цьому виграш визначається як одиниця для найкращого претендента та нуль в інших випадках.

Кандидат визначається як претендент, який під час співбесіди є кращим за всіх попередніх співбесід. Пропустити вживається в значенні «відмовити відразу після співбесіди». Оскільки метою завдання є вибір єдиного найкращого претендента, для прийняття розглядатимуться лише кандидати. «Кандидат» у цьому контексті відповідає поняттю запису в перестановці.

Виведення оптимальної стратегії

Оптимальним підходом для цієї задачі є правило зупину. Згідно з ним, інтерв'юер відхиляє перших r − 1 претендентів (нехай претендент M буде найкращим серед цих r — 1 претендентів), а потім вибирає першого наступного претендента, який кращий за претендента M. Можна показати, що оптимальна стратегія належить цьому класу стратегій^{[джерело?]}. (Зауважте, що ми ніколи не повинні вибирати претендента, який не є найкращим, якого ми бачили досі, оскільки він не може бути найкращим претендентом у цілому). Для довільного r розглянемо ймовірність того, що обрано найкращого претендента.

${\begin{aligned}P(r)&=\sum _{i=1}^{n}P\left({\text{претендент }}i{\text{ відібраний}}\cap {\text{претендент }}i{\text{ найкращий}}\right)\\&=\sum _{i=1}^{n}P\left({\text{претендент }}i{\text{ відібраний}}|{\text{претендент }}i{\text{ is найкращий}}\right)\cdot P\left({\text{претендент }}i{\text{ найкращий}}\right)\\&=\left[\sum _{i=1}^{r-1}0+\sum _{i=r}^{n}P\left(\left.{\begin{array}{l}{\text{найкращий з перших }}i-1{\text{ претендентів}}\\{\text{є серед перших }}r-1{\text{ претендентів}}\end{array}}\right|{\text{претендент }}i{\text{ найкращий}}\right)\right]\cdot {\frac {1}{n}}\\&=\left[\sum _{i=r}^{n}{\frac {r-1}{i-1}}\right]\cdot {\frac {1}{n}}\\&={\frac {r-1}{n}}\sum _{i=r}^{n}{\frac {1}{i-1}}.\end{aligned}}$

Сума не визначена для r = 1, але в цьому випадку єдиною можливою стратегією є вибір першого претендента, отже P(1) = 1/n. Ця сума отримана завдяки спостереженню, що якщо претендент i є найкращим претендентом, тоді він вибирається тоді і тільки тоді, коли найкращий претендент серед перших i − 1 претендентів є серед перших r − 1 претендентів, яких було відхилено. Якщо спрямувати n до нескінченності та позначити $x$ як границю (r−1)/n, використовуючи t замість (i−1)/n і dt замість 1/n, суму можна наблизити інтегралом

$P(x)=x\int _{x}^{1}{\frac {1}{t}}\,dt=-x\ln(x)\;.$

Беручи похідну від P(x) за $x$, прирівнюючи її до 0 та вирішуючи для змінної x, ми знаходимо, що оптимальне x дорівнює 1/e. Таким чином, оптимальна зупинка наближується до n/e зі збільшенням n і найкращий претендент вибирається з імовірністю 1/e.

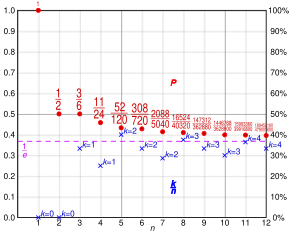
Для малих значень n оптимальне r також можна отримати стандартними методами динамічного програмування. Оптимальні граничні значення r та ймовірність вибору найкращої альтернативи P для кількох значень n наведені в наступній таблиці.

$n$	1	2	3	4	5	6	7	8	9	10
$r$	1	1	2	2	3	3	3	4	4	4
$P$	1.000	0.500	0.500	0.458	0.433	0.428	0.414	0.410	0.406	0.399

Ймовірність вибору найкращого кандидата в класичній проблемі секретаря збігається до $1/e\approx 0.368$.

Альтернативне рішення

Ця задача та кілька її модифікацій можуть бути розв'язані (включно з доказом оптимальності) простим способом за допомогою алгоритму шансів, який також має інші застосування. Модифікації проблеми секретаря, які можна розв'язати за допомогою цього алгоритму, включають випадкову доступність претендентів, більш загальні гіпотези про претендентів, які можуть бути цікавими для особи, яка приймає рішення, групові інтерв'ю претендентів, а також певні моделі для випадкової кількості претендентів^{[джерело?]}.

Обмеження

Розв'язання проблеми секретаря має сенс застосовувати лише тоді, коли є виправданим припущення, що претенденти не знають про застосовану стратегію прийняття рішень, оскільки перші претенденти взагалі не мають шансів і тому можуть не з'явитися на співбесіду.

Одним з важливих недоліків застосування рішення класичної проблеми секретаря є те, що кількість претендентів $n$ має бути відома заздалегідь, що рідко трапляється. Один із способів подолання цієї проблеми — припустити, що кількість заявників є випадковою величиною $N$ із відомим розподілом $P(N=k)_{k=1,2,\cdots }$ (Пресман і Сонін, 1972). Однак для цієї моделі оптимальне рішення, як правило, набагато складніше. Крім того, оптимальна ймовірність успіху тепер вже не близька до 1/e, а зазвичай нижча. Це можна тлумачити як «ціну» за відсутність інформації про кількості претендентів. Однак у цієї моделі ціна висока. Залежно від вибору розподілу $N$, оптимальна ймовірність виграшу може наближатися до нуля. Пошук способів вирішення цієї нової проблеми призвів до нової моделі, яка дає так званий 1/e-закон найкращого вибору.

1/e-закон найкращого вибору

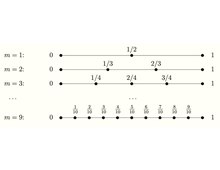
Суть моделі базується на ідеї, що життя є послідовним і що проблеми реального світу виникають у реальному часі. Крім того, легше оцінити проміжки часу, коли конкретні події (прибуття претендентів) мають відбуватися частіше (якщо вони взагалі відбуваються), ніж оцінювати розподіл кількості конкретних подій, які відбуватимуться. Ця ідея призвела до так званого уніфікованого підходу (1984): Модель визначається наступним чином: претендент має бути вибраний на певному часовому інтервалі $[0,T]$ із невідомої кількості $N$ претендентів, які можуть бути оцінені за рейтингом. Мета полягає в тому, щоб максимізувати ймовірність вибору лише найкращих претендентів за гіпотези, що всі послідовності прибуття претендентів різного рангу однаково ймовірні. Припустимо, що всі претенденти мають однакову, але незалежну один від одного щільність функції часу прибуття $f$ на $[0,T]$, і нехай $F$ позначає відповідну функцію розподілу часу прибуття, тобто

$F(t)=\int _{0}^{t}f(s)ds$, $\,0\leq t\leq T$.

Нехай $\tau$ таке, що $F(\tau )=1/e.$ Розглянемо стратегію очікування та спостереження за всіма претендентами до часу$\tau$ а потім виберемо, якщо це можливо, першого кандидата після часу $\tau$, кращого за всіх попередніх. Тоді ця стратегія, яка називається 1/e-стратегія, має такі властивості:

Стратегія 1/e

(i) дає для всіх $N$ ймовірність успіху принаймні 1/e,

(ii) оптимальна стратегія мінімаксу коли $N$ невідомо,

(iii) не вибирає жодного з претендентів (якщо є принаймні один претендент) з імовірністю, яка точно дорівнює 1/e.

1/e-закон, доведений у 1984 році Ф. Томасом Брюссом, став несподіванкою. Причина полягала в тому, що приблизне значення 1/e раніше вважалося недосяжним у моделі для невідомого $N$, тоді як це значення 1/e тепер було досягнуто як нижня межа ймовірності успіху, і це в моделі з, можливо, набагато слабшими гіпотезами (див., наприклад, Math. Reviews 85:m).

Однак існує багато інших стратегій, які досягають (i) і (ii) і, крім того, працюють набагато краще, ніж 1/e-стратегія одночасно для всіх $N$>2. Простим прикладом є стратегія, яка вибирає (якщо це можливо) першого відносно найкращого кандидата після часу $\tau$ за умови, що принаймні один претендент з'явився до цього часу, а в іншому випадку вибирає (якщо це можливо) другого відносно найкращого кандидата після часу $\tau$.

1/e-закон іноді плутають із розв'язком класичної проблеми секретаря, описаної вище, через подібну роль числа 1/e. Однак у 1/e-законі, ця роль є більш загальною. Результат також сильніший, оскільки він справедливий для невідомої кількості претендентів і оскільки модель, заснована на розподілі часу прибуття F є більш сприйнятливою для практичного застосування.

Гра гугол

У статті «Хто вирішив проблему секретаря?» (Фергюсон, 1989), стверджується, що проблема секретаря вперше з'явилася в друкованому вигляді в колонці «Математичні ігри» Мартіна Гарднера в лютому 1960 року в Scientific American:

Попросіть когось взяти довільну кількість аркушів, і на кожному аркуші написати позитивне число. Числа можуть варіюватися від дрібних дробів одиниці до числа гугол (одиниця з сотнею нулів) або навіть більше. Ці аркуші перевертають лицьовою стороною вниз і перемішують на столі. По черзі ви перевертаєте аркуші стороною вгору. Мета полягає в тому, щоб припинити гортати аркуші, коли ви дійдете до числа, яке, на вашу думку, є найбільшим у серії. Ви не можете повернутися назад і вибрати раніше перевернутий аркуш. Якщо ви перегортаєте всі аркуші, то, звичайно, ви повинні вибрати останній.

Фергюсон зазначив, що гра секретаря залишилася невирішеною, як гра з нульовою сумою з двома протидіючими гравцями. У цій грі:

• Аліса, поінформований гравець, таємно пише різні числа на $n$ картках.
• Боб, «зупиняючий» гравець, спостерігає за числами і може припинити перевертання карток коли забажає, виграючи, якщо остання повернута картка має загальну максимальне число.
• Боб хоче вгадати максимальне число з якомога більшою ймовірністю, тоді як мета Аліси полягає в тому, щоб ця ймовірність була якомога нижчою.

Така постановка проблеми має дві відмінності від основної проблеми секретаря:

• Алісі не має записувати числа цілком випадково. Вона може записати їх відповідно до будь-якого спільного розподілу імовірностей щоб ввести в оману Боба.
• Боб спостерігає за фактичними значеннями, написаними на картках, які він може використовувати у своєму процесі прийняття рішень.

Аналіз стратегії

Аліса спочатку записує n чисел, які потім перемішує. Отже, їх порядок не має значення, тобто числа Аліси мають бути випадковою послідовністю змінних $X_{1},X_{2},...,X_{n}$. Тоді стратегія Аліси полягає лише у виборі найскладнішої послідовності випадкових змінних з множини взаємозамінних послідовностей.

Стратегію Боба можна формалізувати як правило зупинки $\tau$ для послідовності $X_{1},X_{2},...,X_{n}$.

Ми кажемо, що правило зупинки $\tau$ для Боба є стратегією зупинки відносного рангу, якщо воно залежить лише від відносних рангів $X_{1},X_{2},...,X_{n}$, а не від їх числових значень. Іншими словами, це еквівалентно тому, що хтось таємно втрутився після того, як Аліса вибрала свої номери, і змінив кожне число в $X_{1},X_{2},...,X_{n}$ на його відносний ранг (впорядковуючи рівні значення довільним чином). Наприклад, $0.2,0.3,0.3,0.1$ змінюється на $2,3,4,1$ або $2,4,3,1$ з рівною ймовірністю. Це еквівалентно тому, якби Аліса застосувала взаємозамінну випадкову перестановку до $\{1,2,...,n\}$. Тепер, оскільки єдина взаємозамінна випадкова перестановка $\{1,2,...,n\}$ — це просто рівномірний розподіл усіх перестановок $\{1,2,...,n\}$, оптимальна стратегія зупинки відносного рангу є оптимальним правилом зупинки для проблеми секретаря, наведеної вище, з ймовірністю виграшу$$Pr(X_{\tau }=\max _{i\in 1:n}X_{i})=\max _{r\in 1:n}{\frac {r-1}{n}}\sum _{i=r}^{n}{\frac {1}{i-1}}$$Тоді мета Аліси полягає в тому, щоб переконатися, що Боб не зможе діяти краще, ніж стратегія зупинки відносного рангу.

Згідно з правилами гри, послідовність Аліси має бути взаємозамінною, але щоб досягти успіху в грі, Аліса не повинна вибирати незалежну послідовність. Якщо Аліса вибере числа незалежно за якимось фіксованим розподілом, це дозволить Бобу грати краще. Щоб зрозуміти це інтуїтивно, уявіть, що $n=2$, і Аліса вибирає обидва числа за нормальним розподілом $N(0,1)$, незалежно один від одного. Тоді якщо Боб перегорне першу картку і побачить $-3$, то він може цілком впевнено перевернути другу картку, а якщо Боб переверне першу картку і побачить $+3$, то він зможе досить впевнено вибирати число на першій картці. Аліса може діяти краще, вибравши $X_{1},X_{2}$ які позитивно корелюють.

Отже, повністю формальна постановка проблеми виглядає так:

Чи існує взаємозамінна послідовність випадкових величин $X_{1},...,X_{n}$, така, що для будь-якого правила зупинки $\tau$, $$Pr(X_{\tau }=\max _{i\in 1:n}X_{i})\leq \max _{r\in 1:n}{\frac {r-1}{n}}\sum _{i=r}^{n}{\frac {1}{i-1}}$$?

Рішення

При $n=2$, якщо Боб грає за оптимальною стратегією зупинок відносного рангу, ймовірність його виграшу становить 1/2. Дивовижно, що для Аліси не існує стратегії мінімаксу, що тісно пов'язане з парадоксом Т. Ковера та парадоксом двох конвертів. Зокрема, Боб може використовувати таку стратегію: генерується випадкове число $Y$. Якщо $X_{1}>Y$, вибирається $X_{1}$, інакше — $X_{2}$. З цією стратегією Боб може виграти з ймовірністю, що перевищує 1/2. Припустімо, що числа Аліси різні, тоді за умови, що $Y\not \in [\min(X_{1},X_{2}),\max(X_{1},X_{2})]$, Боб виграє з імовірністю 1/2, але за умови $Y\in [\min(X_{1},X_{2}),\max(X_{1},X_{2})]$, Боб перемагає з імовірністю 1.

Зауважте, що випадкове число $Y$ можна взяти з будь-якого випадкового розподілу, якщо $Y\in [\min(X_{1},X_{2}),\max(X_{1},X_{2})]$ має ненульову ймовірність.

Однак для будь-якого $\epsilon >0$, Аліса може побудувати взаємозамінну послідовність $X_{1},X_{2}$ так, що ймовірність виграшу Боба становить не більше $1/2+\epsilon$.

Але для $n>2$ відповідь така: Аліса може вибирати випадкові числа (які є залежними випадковими змінними) таким чином, що Боб не може грати краще, ніж за допомогою класичної стратегії зупинки на основі відносних рангів.

Ефективність евристичних методів

Решта статті знову стосується проблеми секретаря для відомої кількості претендентів.

Очікувана ймовірність успіху для трьох евристичних методів

Штейн, Сіл та Рапопорт (2003) вивели очікувані ймовірності успіху для кількох психологічно правдоподібних евристичних методів, які можуть бути використані в проблемі секретаря. Вони досліджували такі евристичні методи:

• Правило відсікання: не приймати жодного з перших y претендентів; після цього вибирати першого наступного претендента (тобто претендента з відносним рангом 1). Це правило має як окремий випадок оптимальну стратегію для класичної проблеми секретаря, для якої y = r.
• Правило підрахунку кандидатів: вибирати y-го претендента. Зауважте, що це правило не обов'язково пропускає претендентів; правило ґрунтується виключно на кількості претендентів, які пройшли співбесіду, а не на будь-якій інформації про претендентів, що залишилися, чи загальному розмірі групи претендентів.
• Правило послідовних невідповідних претендентів: вибрати першого відповідного претендента після співбесід з y невідповідних претендентів (тобто претендентів з відносним рангом > 1).

Кожний евристичний метод має один параметр y. На рисунку (показано праворуч) показано очікувану ймовірність успіху для кожної евристичного метода як функцію y для задач із n = 80.

Варіант з вимірюваним виграшем (англ. Cardinal payoff variant)

Пошук єдиного найкращого кандидата може здатися досить складною метою. Можна уявити, що інтерв'юер скоріше найме претендента з вищим рангом, ніж претендента з нижчим рангом, і не намагатиметься найняти лише найкращого претендента. Тобто інтерв'юер виграє від вибору претендента, який не обов'язково є найкращим, і цей виграш збільшується разом із цінністю обраного претендента.

Щоб змоделювати цю проблему, припустімо, що $n$ претендентів мають «справжні» значення випадкової величини X, згенеровані незалежно і однаково за рівномірним розподілом на [0, 1]. Подібно до класичної проблеми, описаної вище, інтерв'юер тільки спостерігає, чи є кожен претендент на даний момент найкращим (кандидат), повинен відразу прийняти або відхилити кожного претендента, і повинен прийняти останнього претендента, якщо досягнуто кінця списку. (Уточнимо, що, інтерв'юер не дізнається фактичний відносний ранг кожного претендента. Інтерв'юер дізнається лише про те, чи має претендент відносний ранг 1). Однак у цій версії виграш визначається справжньою цінністю обраного претендента. Наприклад, якщо інтерв'юер обирає претендента, справжня цінність якого дорівнює 0,8, то інтерв'юер отримає 0,8. Мета інтерв'юера полягає в тому, щоб максимізувати очікувану цінність обраного претендента.

Оскільки цінність претендентів згенеровано незалежно і однаково за рівномірним розподілом на [0, 1], математичне сподівання t-го претендента, враховуючи, що $x_{t}=\max \left\{x_{1},x_{2},\ldots ,x_{t}\right\}$ визначається як

$E_{t}=E\left(X_{t}|I_{t}=1\right)={\frac {t}{t+1}}.$

Як і в класичній задачі, оптимальна стратегія визначається порогом, який для цієї проблеми ми позначатимемо $c$, за якого інтерв'юер повинен почати приймати претендентів. Берден показав, що c є або $\lfloor {\sqrt {n}}\rfloor$ або $\lceil {\sqrt {n}}\rceil$. (Насправді, це значення, ближче до ${\sqrt {n}}$.) Це випливає з того факту, що враховуючи проблему з $n$ претендентами, очікуваний виграш для деякого довільного порогу $1\leq c\leq n$ є

$V_{n}(c)=\sum _{t=c}^{n-1}\left[\prod _{s=c}^{t-1}\left({\frac {s-1}{s}}\right)\right]\left({\frac {1}{t+1}}\right)+\left[\prod _{s=c}^{n-1}\left({\frac {s-1}{s}}\right)\right]{\frac {1}{2}}={\frac {2cn-{c}^{2}+c-n}{2cn}}.$

Диференціюючи $V_{n}(c)$ за c, отримуємо

${\frac {\partial V}{\partial c}}={\frac {-{c}^{\,2}+n}{2{c}^{\,2}n}}.$

Навчання в парадигмі частково-інформаційного послідовного пошуку. Числа відображають очікувані значення кандидатів на основі їхнього відносного рейтингу (із загальної кількості претендентів m, побачених на даний момент) у різних точках пошуку. Очікування розраховуються на основі випадку, коли їх значення рівномірно розподілені між 0 і 1. Інформація про відносний ранг дозволяє інтерв'юеру точніше оцінювати претендентів, оскільки вони накопичують більше точок даних для їх порівняння.

Оскільки $\partial ^{\,2}V/\partial c^{\,2}<0$ для всіх допустимих значень $c$, ми знаходимо, що $V$ максимізується при $c={\sqrt {n}}$. Оскільки V є опуклою функцією у $c$, оптимальним цілочисельним порогом має бути $\lfloor {\sqrt {n}}\rfloor$ або $\lceil {\sqrt {n}}\rceil$. Таким чином, для більшості значень $n$ інтерв'юер почне приймати претендентів раніше у версії з вимірюваним виграшем, ніж у класичній версії, де метою є вибір єдиного найкращого претендента. Зауважте, що це не асимптотичний результат: він справедливий для всіх $n$. Цікаво, що якщо кожен із $n$ претендентів має фіксоване окреме значення від $1$ до $n$, тоді $V$ максимізується при $c={\sqrt {n}}-1$, з тими самими міркуваннями щодо опуклості, що й раніше. Для інших відомих розподілів оптимальну стратегію можна розрахувати за допомогою динамічного програмування.

Більш загальна форма цієї проблеми, запропонована Пеллі та Кремером (2014), передбачає, що під час інтерв'ю з новим претендентом, інтерв'юер порівнює рейтинг претендента відносно всіх претендентів, яких опитували раніше. Ця модель узгоджується з уявленнями про те, що інтерв'юер навчається, продовжуючи процес пошуку, накопичуючи набір минулих даних, які можна використовувати для оцінки нових претендентів. Перевага цієї так званої часткової інформаційної моделі полягає в тому, що рішення та результати, досягнуті з урахуванням інформації про відносний ранг, можна безпосередньо порівняти з відповідними оптимальними рішеннями та результатами, якби інтерв'юер отримав повну інформацію про цінність кожного претендента. Цей варіант проблеми з повною інформацією, в якій претендентів відбирають незалежно від відомого розподілу, а інтерв'юер прагне максимізувати очікувану цінність обраного кандидата, спочатку розв'язали Мозер (1956), Сакагучі (1961) і Карлін (1962).

Інші варіанти задачі

Є кілька варіантів задачі секретаря, які також мають прості та елегантні рішення.

Вибір другого найкращого претендента з однієї спроби

Один варіант замінює мету вибору найкращого претендента на мету вибору другого найкращого. Роберт Дж. Вандербей називає це проблемою «випускників аспірантури», стверджуючи, що «найкращі» випускники підуть до Гарварду. Для цієї задачі ймовірність успіху для парної кількості заявників дорівнює ${\frac {0.25n^{2}}{n(n-1)}}$. Ця ймовірність прямує до 1/4 коли n прямує до нескінченності, ілюструючи той факт, що легше вибрати найкращого претендента, ніж другого за найкращим.

Вибір k кращих претендентів, використовуючи k спроб

Розглянемо задачу вибору k найкращих претендентів з n претендентів, використовуючи k спроб.

Загалом, метод оптимального прийняття рішення починається зі інтерв'ю з $r=\left\lfloor {\frac {n}{ke^{1/k}}}\right\rfloor$ претендентами, жоден з яких не вибирається; потім вибирається кожний претендент, який є кращим за перших $r$ претендентів, доки список претендентів не буде вичерпано або не буде обрано найкращих k претендентів. Якщо $k$ залишається постійним, коли $n\to \infty$, то ймовірність успіху збігається до ${\frac {1}{ek}}$. Відповідно до Вандербея (1980), якщо $k=n/2$, то ймовірність успіху дорівнює ${\frac {1}{n/2+1}}$.

Вибір найкращого претендента, використовуючи кілька спроб

У цьому варіанті гравець має $r$ спроб і виграє, якщо будь-який вибір є найкращим. Оптимальна стратегія для цієї проблеми належить до класу стратегій, визначених набором порогових чисел $(a_{1},a_{2},...,a_{r})$, where $a_{1}>a_{2}>\cdots >a_{r}$.

Зокрема, уявіть, що у вас є $r$ листів про прийняття на роботу, позначених від $1$ до $r$. У вас буде $r$ службовців з найму, кожен з яких триматиме по одному листу. Ви продовжуєте проводити співбесіди з претендентами та розміщуєте їх у таблиці, яку бачить кожен зі службовців. Тепер службовець $i$ надішле свій лист про прийняття на роботу першому кандидату, який є кращим за всіх кандидатів від $1$ до $a_{i}$. (Невикористані листи про прийняття за замовчуванням надаються останнім претендентам, як і в стандартній проблемі секретаря).

При $n\rightarrow \infty$, кожне $a_{i}\sim ne^{-k_{i}}$, для деякого раціонального числа $k_{i}$.

Імовірність виграшу

Коли $r=2$, ймовірність виграшу збігається до $e^{-1}+e^{-{\frac {3}{2}}},(n\rightarrow \infty )$. Загалом, для додатних цілих чисел $r$, ймовірність виграшу збігається до $p_{1}+p_{2}+\cdots +p_{r}$, де $p_{i}=\lim _{n\rightarrow \infty }{\frac {a_{i}}{n}}$.

Гілберт, Мостеллер (1966) обчислили ймовірність до $r=4$, де $e^{-1}+e^{-{\frac {3}{2}}}+e^{-{\frac {47}{24}}}+e^{-{\frac {2761}{1152}}}$.

Matsui, Ano (2016) запропонували загальний алгоритм. Наприклад, $p_{5}=e^{-{\frac {4162637}{1474560}}}$.

Експериментальні дослідження

Психологи-експериментатори та економісти вивчали поведінку реальних людей щодо прийняття рішень в ситуаціях, схожих на проблему секретаря. Значною мірою ця робота показала, що люди, як правило, припиняють пошук надто рано. Принаймні частково це можна пояснити вартістю оцінювання претендентів. Це може свідчити про те, що у реальному світі люди недостатньо довго чекають, коли стикаються з проблемами, де альтернативи рішення зустрічаються послідовно. Наприклад, намагаючись вирішити, на якій автозаправній станції вздовж шосе зупинитися, щоб заправити автомобіль, люди можуть зупинитися раніше, ніж слід. В цьому випадку, вони, як правило, платять за паливо більше, ніж якби вони шукали довше. Те ж саме може бути вірно, коли люди шукають авіаквитки в Інтернеті. Експериментальне дослідження таких проблем, як проблема секретаря, іноді називають дослідженням поведінкових операцій.

Нейронні кореляти

Хоча є багато нейронаукових досліджень щодо інтеграції інформації, або репрезентації переконань у завданнях сприйняття рішень тваринами і людьми, відносно мало відомо про те, як приймається рішення припинити збір інформації.

Дослідники вивчали нейронні основи вирішення проблеми секретаря у здорових добровольців за допомогою функціональної МРТ. Марковський процес вирішування використовувався для кількісного визначення цінності продовження пошуку в порівнянні з поточним варіантом. Рішення прийняти чи відхилити варіант залучали тім'яну та дорсолатеральну префронтальну кору, а також смугасте тіло, острівцеву кору та передню поясну частину. Таким чином, області мозку, які раніше були залучені до інтеграції доказів і представлення винагород кодують значення порогів, які викликають рішення про вибір.

Історія

Ймовірно, проблема секретаря була представлена ​​в 1949 році Меррілом М. Фладом, який назвав її проблемою нареченої в лекції, яку він прочитав того року. Він кілька разів посилався на цю проблему протягом 1950-х років, наприклад, у виступі на конференції в Пердью 9 травня 1958 року, і згодом вона стала широко відомою у фольклорі, хоча в той період нічого не було опубліковано. У 1958 році він надіслав листа Леонарду Гіллману, і приблизно дюжину копій друзям, у тому числі Семюелю Карліну та Дж. Роббінсу, з описом доказу оптимальної стратегії з додатком Р. Палермо, який довів, що серед усіх стратегій домінує стратегія, яку можна сформулювати як «беззастережно відхилити перших p претендентів, потім прийняти наступного претендента, який кращий з перших p».

Першу публікацію, ймовірно, зробив Мартін Ґарднер в журналі Scientific American в лютому 1960 року. Він дізнався про задачу секретаря від Джона Х. Фокса молодшого та Л. Джеральда Марні, які незалежно один від одного придумали еквівалентну проблему в 1958 році; вони назвали її «грою гугол». Фокс і Марні не мали оптимального рішення; Гарднер звернувся за порадою до Лео Мозера, який (разом з Дж. Р. Паундером) надав коректний аналіз для публікації в журналі. Незабаром після цього кілька математиків написали Гарднеру, щоб розповісти йому про еквівалентну проблему, про яку вони дізналися в неофіційних розмовах, і всі ці чутки, швидше за все, можна простежити до оригінальної роботи Флада.

1/e-закон найкращого вибору належить Ф. Томасу Брюссу.

Фергюсон має велику бібліографію та вказує на те, що подібну (але іншу) проблему розглядав Артур Кейлі 1875 році, а ще раніше Йоганн Кеплер який витратив 2 роки на дослідження 11 кандидатів на шлюб протягом 1611—1613 років після смерті його першої дружини.

Комбінаторне узагальнення

Проблему секретаря можна узагальнити на випадок, коли є кілька різних робіт. Так само, є $n$ претендентів, які з'являються у випадковому порядку. Коли претендент з'являється, він відкриває набір невід'ємних чисел. Кожне значення визначає його кваліфікацію для однієї з робіт. Адміністратор повинен не тільки прийняти рішення про те, брати претендента на роботу чи ні, але і призначити його на одну з вакансій на постійній основі. Мета полягає в тому, щоб знайти і призначити претендентів так, щоб сума кваліфікацій була якомога більшою. Ця проблема ідентична пошуку відповідності максимальної ваги в двочастковому графі зі зваженими ребрами, де $n$ вузлів однієї сторони з'являються у випадковому порядку. Таким чином, це окремий випадок онлайн-проблеми двочасткового зіставлення.

Шляхом узагальнення класичного алгоритму для проблеми секретаря можна отримати призначення, де очікувана сума кваліфікацій лише в $e$ разів менше, ніж оптимальне (офлайн) призначення.

Див. також

• Задача про призначення
• Алгоритм шансів
• Оптимальна зупинка
• Проблема Роббінса
• Теорія пошуку
• Проблема стабільних шлюбів

Посилання

• С. М. Гусейн-Заде. Разборчивая невеста. Библиотека «Математическое просвещение», том 25, МЦНМО, 2003 ISBN 5-94057-076-3
• С. М. Гусейн-Заде. Разборчивая невеста. Видео-лекция. Малый мехмат, МГУ, 30.11.2002.
• Bearden, J.N. (2006). A new secretary problem with rank-based selection and cardinal payoffs. Journal of Mathematical Psychology (англ.). 50: 58—9. doi:10.1016/j.jmp.2005.11.003.
• Bearden, J.N.; Murphy, R.O.; Rapoport, A. (2005). A multi-attribute extension of the secretary problem: Theory and experiments. Journal of Mathematical Psychology. 49 (5): 410—425. CiteSeerX 10.1.1.497.6468. doi:10.1016/j.jmp.2005.08.002. S2CID 9186039.
• Bearden, J. Neil; Rapoport, Amnon; Murphy, Ryan O. (September 2006). Sequential Observation and Selection with Rank-Dependent Payoffs: An Experimental Study. Management Science. 52 (9): 1437—1449. doi:10.1287/mnsc.1060.0535.
• Bruss, F. Thomas (June 2000). Sum the odds to one and stop. The Annals of Probability. 28 (3): 1384—1391. doi:10.1214/aop/1019160340.
• Bruss, F. Thomas (October 2003). A note on bounds for the odds theorem of optimal stopping. The Annals of Probability. 31 (4): 1859—1961. doi:10.1214/aop/1068646368.
• Bruss, F. Thomas (August 1984). A Unified Approach to a Class of Best Choice Problems with an Unknown Number of Options. The Annals of Probability (англ.). 12 (3): 882—889. doi:10.1214/aop/1176993237.
• Flood, Merrill R. (1958). Proof of the optimum strategy (англ.). Лист Martin Gardner. Martin Gardner papers series 1, box 5, folder 19: Stanford University Archives.
• Freeman, P.R. (1983). The secretary problem and its extensions: A review. International Statistical Review / Revue Internationale de Statistique. 51 (2): 189—206. doi:10.2307/1402748. JSTOR 1402748.
• Gardner, Martin (1966). 3. New Mathematical Diversions from Scientific American (англ.). Simon and Schuster. [reprints his original column published in February 1960 with additional comments]
• Girdhar, Yogesh; Dudek, Gregory (2009). Optimal Online Data Sampling or How to Hire the Best Secretaries. 2009 Canadian Conference on Computer and Robot Vision (англ.). с. 292—298. CiteSeerX 10.1.1.161.41. doi:10.1109/CRV.2009.30. ISBN 978-1-4244-4211-9. S2CID 2742443.
• Gilbert, J; Mosteller, F (1966). Recognizing the Maximum of a Sequence. Journal of the American Statistical Association (англ.). 61 (313): 35—73. doi:10.2307/2283044. JSTOR 2283044.
• Gnedin, A. (1994). A solution to the game of Googol. Annals of Probability (англ.). 22 (3): 1588—1595. doi:10.1214/aop/1176988613.
• Gnedin, A. (2021). The best choice problem with random arrivals: How to beat the 1/e-strategy. Stochastic Processes and Their Applications (англ.). 145: 226—240. doi:10.1016/j.spa.2021.12.008. S2CID 245449000.
• Hill, T.P. «Knowing When to Stop». American Scientist, Vol. 97, 126—133 (2009). (For French translation, see cover story in the July issue of Pour la Science (2009))
• Ketelaar, Timothy; Todd, Peter M. (2001). Framing Our Thoughts: Ecological Rationality as Evolutionary Psychology's Answer to the Frame Problem. Conceptual Challenges in Evolutionary Psychology. Studies in Cognitive Systems. Т. 27. с. 179—211. doi:10.1007/978-94-010-0618-7_7. ISBN 978-94-010-3890-4.
• Matsui, T; Ano, K (2016). Lower bounds for Bruss' odds problem with multiple stoppings. Mathematics of Operations Research (англ.). 41 (2): 700—714. arXiv:1204.5537. doi:10.1287/moor.2015.0748. S2CID 31778896.
• Sardelis, Dimitris A.; Valahas, Theodoros M. (March 1999). Decision Making: A Golden Rule. The American Mathematical Monthly. 106 (3): 215. doi:10.2307/2589677. JSTOR 2589677.
• Seale, D.A.; Rapoport, A. (1997). Sequential decision making with relative ranks: An experimental investigation of the 'secretary problem'. Organizational Behavior and Human Decision Processes. 69 (3): 221—236. doi:10.1006/obhd.1997.2683.
• Stein, W.E.; Seale, D.A.; Rapoport, A. (2003). Analysis of heuristic solutions to the best choice problem. European Journal of Operational Research (англ.). 151: 140—152. doi:10.1016/S0377-2217(02)00601-X.
• Vanderbei, R. J. (November 1980). The Optimal Choice of a Subset of a Population. Mathematics of Operations Research (англ.). 5 (4): 481—486. doi:10.1287/moor.5.4.481.
• Vanderbei, Robert J. (2012). The postdoc variant of the secretary problem (PDF) (Звіт). CiteSeerX 10.1.1.366.1718.

Посилання

• OEIS Number of daughters to wait before picking in sultan's dowry problem with n daughters.
• Weisstein, Eric W. Sultan's Dowry Problem(англ.) на сайті Wolfram MathWorld.
• Neil Bearden. Optimal Search (Secretary Problems). Архів оригіналу за 4 January 2017.
• Optimal Stopping and Applications book by Thomas S. Ferguson